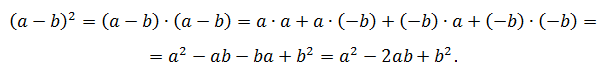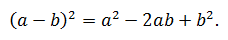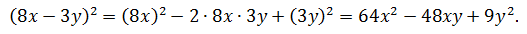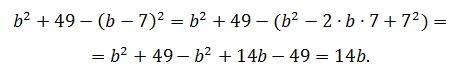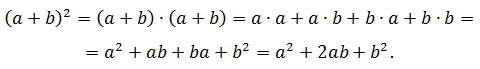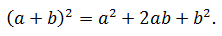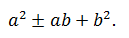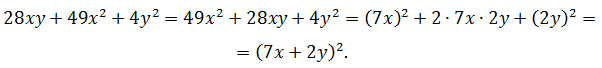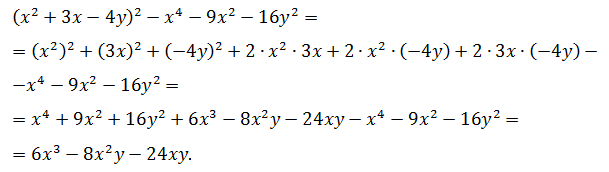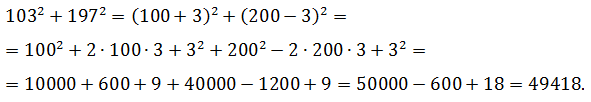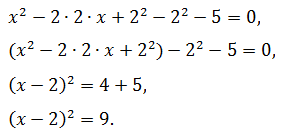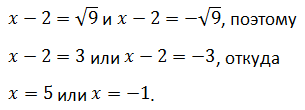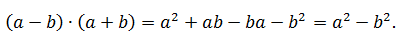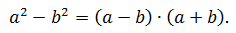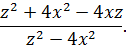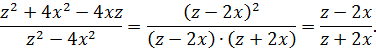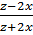Что значит неполный квадрат разности
Сокращенное умножение: правила, формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
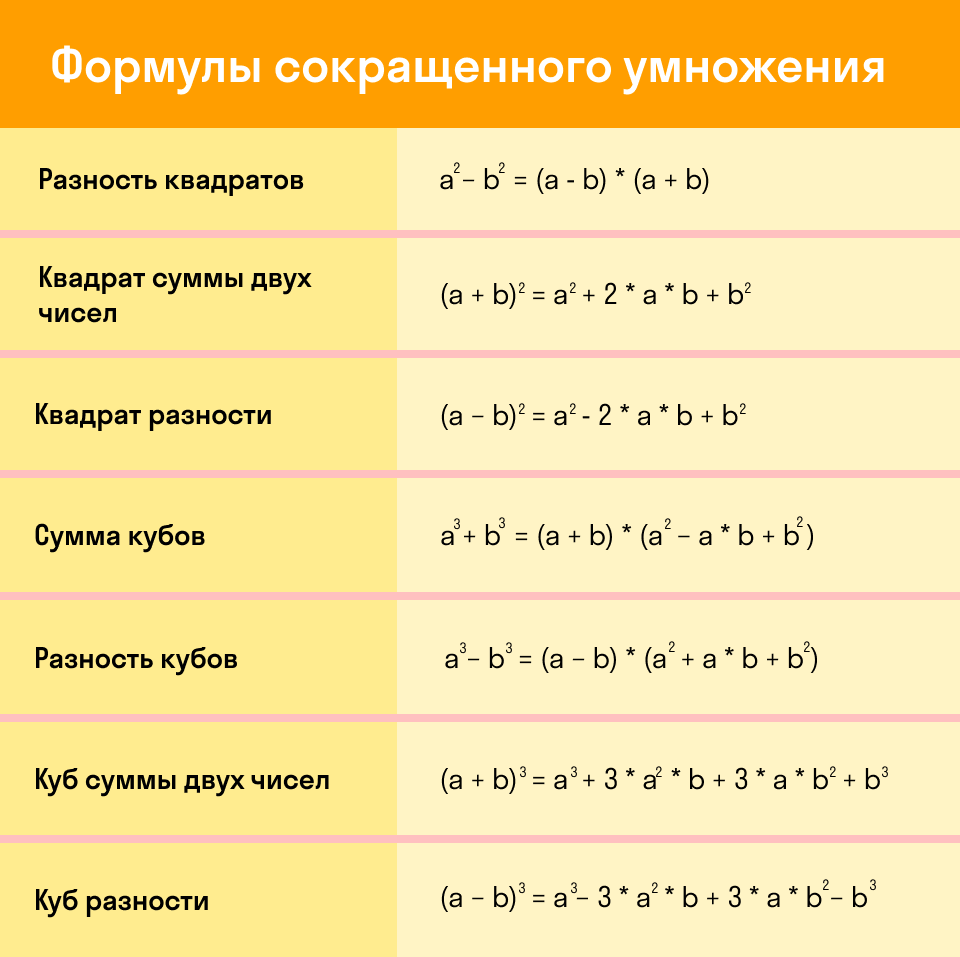
Формулы сокращенного умножения
Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.
Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.
Как читать формулы сокращенного умножения
Учимся проговаривать формулы сокращенного выражения:
Обучение на курсах по математике — дорога к хорошим оценкам в школе и высокому баллу на экзамене.
Доказательство формул сокращенного умножения
Остальные ФСУ можно доказать аналогичным методом.
Дополнительные формулы сокращенного умножения
К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.
Бином Ньютона
Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:
Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:
ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
a n − b n = (a − b) * (a n-1 + a n-2 * b + a n-3 * b 2 + … + a * b n-2 + b n-1 ).
Для четных показателей можно записать так:
a 2*m − b 2*m = (a 2 − b 2 ) *(a 2*m−2 + a 2*m−4 * b 2 + a 2*m−6 * b 4 + … + b 2*m−2 ).
Для нечетных показателей:
a 2*m+1 − b 2*·m+1 = (a − b) * (a 2*m + a 2*m−1 * b + a 2*m−2 * b 2 + … + b 2*m ).
Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.
Решение задач
Давайте потренируемся и рассмотрим примеры с дробями.
Задание 1
Как решаем: воспользуемся формулой квадрата суммы: (55 + 10) 2 = 55 2 + 2 * 55 * 10 + 10 2 = 3025 + 1100 + 100 = 4225.
Задание 2
Что сделать: упростить выражение 64 * с 3 – 8.
Как решаем: применим разность кубов: 64 * с 3 – 8 = (4 * с) 3 – 2 3 = (4 * с – 2)((4 * с) 2 + 4 * с * 2 + 2 2 ) = (4 * с – 2)(16 * с 2 + 8 * с + 4).
Задание 3
Как решаем:
Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂
Формулы сокращённого умножения
При выполнении преобразований разных выражений часто встречаются некоторые частные случаи умножения. Равенства, выражающие эти случаи, называются формулами сокращённого умножения.
Формулы сокращённого умножения — это выражения, в которых пропущены промежуточные вычисления, поэтому их и называют сокращёнными.
Обратите внимание, что a и b в формулах сокращённого умножения могут быть как числами, так и выражениями.
Разложение формул сокращенного умножения
Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения.
Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:
Доказательство: выполним преобразование правой части формулы, приведём подобные члены и получим левую часть формулы:
Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа:
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе число, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
Неполный квадрат суммы
это квадрат суммы, которое также называется полным квадратом суммы, относительно выражения:
которое называется неполным квадратом суммы. Неполный квадрат суммы — это сумма квадратов двух чисел и их произведения. Неполный квадрат суммы отличается от полного только произведением чисел, которое не удваивается.
Неполный квадрат разности
это квадрат разности, который также называется полным квадратом разности относительно выражения:
которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.
Неполный квадрат разности
Неполный квадрат разности в алгебре важен в качестве составной части формулы суммы кубов. В процессе изучения формул сокращенного умножения важно научиться видеть формулы полных и неполных квадратов и различать их между собой.
Неполный квадрат разности — это сумма трех слагаемых, два из которых — квадраты некоторых выражений, а третье равно произведению этих выражений (со знаком «минус» перед ним).
В отличие от полного квадрата разности, произведение выражений не удваивается.
С помощью букв неполный квадрат разности можно записать так:
С помощью схемы — так:
Примеры неполных квадратов разности:
На практике неполный квадрат, как правило, свернут, поэтому, чтобы понять, является ли выражение неполным квадратом разности, его нужно проанализировать.
На этапе изучения новой темы есть смысл выражения подробно расписывать.
Как определить, является ли выражение неполным квадратом разности?
Признаки неполного квадрата разности
1) Выражение состоит ровно из трех слагаемых.
2) Два положительных слагаемых представляют собой квадраты некоторых выражений.
3) Третье слагаемое со знаком «минус» перед ним равно произведению этих выражений.
16x²=(4x)², 81y²=(9y)². Проверяем, равно ли третье слагаемое произведению 4x и 9y: 4x∙9y=36xy — да, равно. Следовательно, это выражение — неполный квадрат разности.
С помощью схемы это можно записать так:
100c²=(10c)², d² — уже представлен как квадрат, но 10c∙d≠20cd, поэтому выражение неполным квадратом разности не является (так как 20cd=2∙10c∙d, это выражение — полный квадрат разности).
Слагаемые могут стоять в произвольном порядке.
В некоторых случаях выражение, не являющееся неполным квадратом разности, может быть к нему приведено.
Здесь два слагаемых отрицательны, значит, неполным квадратом разности это выражение быть не может. Но если знак «минус» вынести за скобки, все знаки в скобках изменятся на противоположные:
В скобках — неполный квадрат разности.
В алгебре очень важно уметь раскладывать многочлены на множители и преобразовывать выражения (в том числе, по формуле суммы кубов, частью которой является неполный квадрат разности).
Для успешного решения математических задач часто бывает необходимо уметь преобразовывать созданные выражения. Для этого применяют базовые знания, формулы сокращённого умножения, в том числе, квадрат суммы и квадрат разности.
Они помогают упрощать громоздкие записи, более рационально подходить к приведению дробей к одному знаменателю, решению уравнений и задач по геометрии, тригонометрии, математическому анализу, физике, химии, экономическим дисциплинам и многим другим наукам.
Поэтому среди многих разделов математики школьная алгебра занимает базовую приоритетную позицию, дающую основы вычислений для смежных предметов.
Формула квадрата разности
Для получения формулы применяют правило умножения многочлена на многочлен: нахождение суммы произведений каждого слагаемого одной скобки на каждое слагаемое второй скобки, учитывая, что квадрат отрицательного числа равен квадрату положительного:
Если запомнить правило, то необходимость постоянно прописывать эту цепочку равенств исчезает.
Квадрат разности двух выражений равен сумме квадратов каждого из выражений без их удвоенного произведения:
Примеры задач с решением
Задача №1
При использовании формулы получается:
Задача №2
Формула квадрата суммы и неполного квадрата суммы
Также легко, как и в предыдущем случае, выводится эта формула:
Квадрат суммы двух выражений равен сумме квадратов каждого из них плюс их удвоенное произведение:
Многие школьники, начинающие знакомиться с этим материалом, часто теряют двойку во втором слагаемом правой части, получая
Однако, в этом случае, возникает неполный квадрат суммы (или разности), который на множестве действительных чисел не раскладывается на множители.
Обе формулы применяются не только для раскрытия скобок, но и для разложения на множители, что в свою очередь упрощает приведение к одному знаменателю, сокращение дробей, решение уравнений высоких степеней.
Примеры задач с решением
Задача №3
Преобразовать трёхчлен в квадрат двучлена:
Поскольку квадраты находятся на втором и третьем местах, поменяем слагаемые между собой и подготовим выражение для применения формулы:
Возведение во вторую степень суммы трёх и более слагаемых выполняется аналогично: необходимо возвести в квадрат каждый элемент, записать все возможные удвоенные произведения и сложить полученные результаты.
Правила возведения в степени более высоких порядков возникают, когда выполняется умножение одинаковых многочленов несколько раз.
Возможность выполнять возведение в квадрат больших чисел, не используя калькулятор, является одним из преимуществ сокращённого умножения.
Задача №4
Выполнить раскрытие скобок и упростить:
Задача №5
Для каждого слагаемого применяется одно из правил возведения в квадрат, затем производится суммирование результатов:
Решая квадратные уравнения, вместо поиска дискриминанта выделяют полный (точный) квадрат среди слагаемых, расположенных в левой части. В правую сторону собираются оставшиеся элементы.
Задача №6
Первые два слагаемых левой части полностью удовлетворяют формуле квадрата суммы. Соотнеся их с соответствующими элементами правила, определяют, прибавляют и вычитают третье, затем сворачивают в точный квадрат, остальные члены алгебраической суммы переносят в правую сторону:
Решениями исходного уравнения являются корни уравнений
Разность квадратов
Ещё одной формулой сокращённого умножения является разность квадратов. Она получается при умножении суммы двух выражений на их разность.
Читается справа налево.
Разность квадратов двух выражений равна произведению разности этих выражений на их сумму:
Применение последней записи справа налево есть раскрытие скобок более удобным способом, чем простое умножение многочленов.
Разложение на множители позволяет судить о наличии целых или натуральных корней квадратного уравнения.
Пример задачи с решением
Задача №7
В числителе записан квадрат разности, а в знаменателе – разность квадратов двух выражений. Применяя соответствующие формулы, получается искомый результат:
В большинстве случаев разницы, как сворачивать квадрат двучлена, не существует. Однако в данной ситуации, благодаря выражению в знаменателе, на первое место лучше поставить
Онлайн калькуляторы помогают выполнять преобразования. Однако, поскольку формулы сокращённого умножения являются базовым материалом школьного курса, то лучше не просто получить результат, но и понять, каким образом к нему пришли.
Формулы сокращенного умножения.
Математические выражения (формулы) сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне не заменимы во многих областях точных наук. Эти 7 символьных записей не заменимы при упрощении выражений, решении уравнений, при умножении многочленов, сокращении дробей, решении интегралов и многом другом. А значит будет очень полезно разобраться как они получаются, для чего они нужны, и самое главное, как их запомнить и потом применять. Потом применяя формулы сокращенного умножения на практике самым сложным будет увидеть, что есть х и что есть у. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.
Четвертая (х + у) 3 = х 3 + 3х 2 у + 3ху 2 + у 3. Чтобы вычислить куб суммы двух выражений нужно к кубу первого выражения прибавить утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
Шестая х 3 + у 3 = (х + у) (х 2 — ху + у 2 ) Чтобы высчитать сумму кубов двух выражений нужно умножить суммы первого и второго выражения на неполный квадрат разности этих выражений.
Не сложно запомнить, что все формулы применяются для произведения расчетов и в противоположном направлении (справа налево).
О существовании этих закономе рностей з нали еще около 4 тысяч лет тому назад. Их широко применяли жители древнего Вавилона и Египта. Но в те эпохи они выражались словесно или геометрически и при расчетах не использовали буквы.
Первым эту математическую закономерность доказал древнегреческий учёный Евклид, работавший в Александрии в III веке до н.э., он использовал для этого геометрический способ доказательства формулы, так как буквами для обозначения чисел не пользовались и учёные древней Эллады. Ими повсеместно употреблялись не “а 2 ”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник, заключенный между отрезками a и b”.
И так Евклид взял квадрат со стороной (a + b):
С другой стороны, этот же квадрат он представить иначе, разделив сторону на а и b:
Тогда площадь квадрата можно представить в виде суммы площадей:
И так как квадраты были одинаковы, то их площади равны, и это значит:
Таким образом, была доказана геометрически формула квадрата суммы.