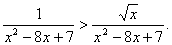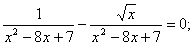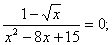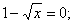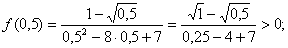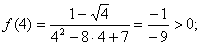Что значит найти множество значений неравенства

Основные методы решения неравенства.

Неравенством называется запись, в которой функции соединены знаком (или несколькими знаками) отношения «>», » g(x),

f(x) g(x), f(x) g(x) является всякое значение переменной x = a, при котором справедливо неравенство
f(a) > g(a), или функция f(x) при x = a принимает большее значение чем функция g(x).

Задание «решить неравенство» означает, что требуется найти множество всех его решений. Это множество может оказаться пустым — в случае, когда решений нет. Множество всех решений неравенства будем называть его ответом.

Неравенство В называется следствием неравенства А, если всякое решение А является решением неравенства В. В этом случае используется запись АВ. Два неравенства А и В называются равносильными (или эквивалентными пишем
АВ либо А

В), если их ответы совпадают. Если АВ и ВА, то неравенства А и В эквивалентны.

Запись нескольких неравенств под знаком фигурной скобки называется системой (число и вид неравенств, входящих в систему, может быть произвольным). Решение системы неравенств есть пересечение решений всех входящих в нее неравенств. Двойное неравенство f(x) 1.

Теперь, решаем систему неравенств:

2. Если обе части неравенства умножить на положительную функцию, определенную в ОДЗ данного неравенства (или на положительное число), то получим неравенство, равносильное исходному неравенству:

если f(x) > g(x) и h(x) > 0, то f(x)h(x) > g(x)h(x)

3. Если обе части неравенства умножить на отрицательную функцию, определенную в ОДЗ данного неравенства (или на отрицательное число) и знак неравенства изменить на противоположный, то полученное неравенство эквивалентно данному неравенству:

если f(x) > g(x) и h(x) g(x) и m(x) > h(x), то f(x) + m(x) > g(x) + h(x).

7. Неравенства, образованные неотрицательными функциями, можно почленно возводить в положительную степень:

Пусть M – множество допустимых значений переменной х данного неравенства (ОДЗ). B – множество найденных решений неравенства. A множество решений данного неравенства. Тогда A = BM.

Вычтем из обеих частей неравенства функцию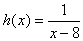получим неравенство 3х > 9.

Разделим обе части полученного неравенства на положительное число 3 в результате получим x > 3 (2). Выполнив это преобразование, мы заменили неравенство (1) неравенством (2). Эти неравенства не равносильны.(1)(2).

M = (-; 8)(8; +)- ОДЗ неравенства (1).

Найдем множество решений неравенства (1)

A = BM =((-; 8)(8; +)(3; +) = (3; 8)(8; +),

Ответ: x(3; 8)(8; +).

Метод интервалов часто используют при решения неравенств. Он позволяет свести решение неравенства f(x) > 0 ( ) к решению уравнения f(x) = 0.

Метод заключается в следующем:

1.Находится ОДЗ неравенства.

2.Неравенство приводится к виду f(x) > 0( ) (т.е. правая часть переносится влево) и упрощается.

3.Решается уравнение f(x) = 0.

4.На числовой оМетод интервалов часто используют при решения неравенств. Он позволяет свести решение неравенства f(x) > 0 (, (-5; +).

Пример 4. Решить неравенство

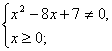
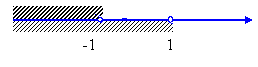
Используя свойство частного и определение квадратного корня делаем вывод, чтооткудаОДЗ: x(0; 1)(1; 7)(7; +)

На промежутке (0;1) возьмем точку 0,5;

На промежутке (1; 7) возьмем точку 4,

На промежутке (7; +) возьмем точку 9,

Расставим знаки на координатной прямой.

Таким образом, решением данного неравенства является множество чисел принадлежащих промежутку (0; 1)(1; 7)

Эти примеры наглядно демонстрируют, что промежутки знакопостоянства не обязательно чередуются, процесс определения знака на промежутке может оказаться довольно трудной задачей.

Полезно запомнить следующее.

Если функция представляет собой произведение нескольких не повторяющихся множителей, имеющих вид (ax + b), где a > 0, то знаки функции на промежутках справа на лево чередуются с «плюса» на «минус». Если какой-то множитель повторяется четное число раз, то при переходе через эту точку смены знака не происходит. В примере №4 Такой точкой была точка 1

Источник

Решение неравенств в школьном курсе математики

Автор: Булякова Алия Рашитовна

Решение неравенств в школьном курсе математики

Решить неравенство – это значит найти множество его решений. Два неравенства называют равносильными, если их множества решений совпадают.

Областью допустимых значений (ОДЗ) неравенства называют общую часть (пересечение) областей определения функций, входящих в неравенство.

Множеством решений неравенства называют множество всех значений неизвестного х, при подстановке которых в неравенство получается верное числовое неравенство. Сами эти значения называют решениями неравенства.

Процесс решения неравенства – это цепочка равносильных переходов от исходного к такому неравенству, множество решений которого известно или легко может быть найдено.

Однако это не всегда удаётся сделать. В процессе неравносильных преобразований могут появиться как посторонние решения, так и может происходить потеря решений. Причём в отличие от уравнений, для неравенств всё обстоит значительно сложнее. Это будет показано в последующих примерах, которые будут рассмотрены в работе.

Поэтому при решении неравенств равносильные преобразования нужно выполнять аккуратно, следить за тем, чтобы не выйти за ОДЗ исходного неравенства или не потерять его часть.

Наиболее распространённые преобразования, приводящие к равносильным неравенствам (обратите внимание на связь этих утверждений со свойствами числовых неравенств):

1. Если к обеим частям неравенства прибавить одну и туже функцию, определённую на ОДЗ, то получим неравенство равносильное исходному.

2. Если обе части неравенства умножить или разделить на одну и туже функцию, все значения которой в ОДЗ положительны (отрицательны), то получим неравенство, равносильное исходному (то изменив знак неравенства на противоположный, получим неравенство равносильное данному).

Это более простые («безопасные») ситуации, а теперь рассмотрим более «коварные» случаи.

4. Как и при решении уравнений, неприятности могут происходить в точках обращения в ноль общего множителя левой и правой части. Эти точки ОДЗ заслуживают отдельного рассмотрения. В случае строгих неравенств они не являются решениями, а в случае нестрогих неравенств такие значения являются решениями.

5. В отличии от уравнений, « коварными» являются и точки ОДЗ, в которых общий множитель отличен от нуля, так как при умножении (делении) обеих частей неравенства на положительное число или выражение знак неравенства сохраняется, а на отрицательный – меняется на противоположный. Поэтому приходится выделять эти подслучаи.

6. При решении неравенства (особенно иррациональных) часто возникает необходимость возведения обеих частей неравенства в квадрат (чётную степень). Это самая опасная ситуация, так как:

а) если обе части неравенства неотрицательны, то обе части неравенства для таких значений неизвестного можно возвести в квадрат (чётную степень), сохраняя знак неравенства;

б) если обе части неравенства имеют разные знаки, то при таких значениях неравенства нельзя обе части неравенства возводить в квадрат (четную степень), да и не нужно, так как сразу ясно, являются или не являются решением неравенства значения неизвестного, реализующие эту ситуацию. Таким образом, при необходимости возведения обеих частей неравенства в квадрат (четную степень) приходиться выделять эти под случаи, проверять решения для них отдельно.

Источник

Метод интервалов, решение неравенств

Определение квадратного неравенства

Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти множество, для которых оно выполняется.

Квадратное неравенство выглядит так:

Квадратное неравенство можно решить двумя способами:

Решение неравенства графическим методом

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.

Как дискриминант влияет на корни уравнения:

Решение неравенства методом интервалов

Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.

Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.

Если неравенство со знаком

Плюс или минус: как определить знаки

Можно сделать вывод о знаках по значению старшего коэффициента a:

если a > 0, последовательность знаков: +, −, +,

если a 0, последовательность знаков: +, +,

Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.

Неравенство примет вид:

В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.

Отобразим эти данные на чертеже:

2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.

Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Пример 2. Применить метод интервалов для решения неравенства х2+4х+3

Источник

Решение линейных неравенств

Основные понятия

Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.

Линейные неравенства — это неравенства вида:

где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит сделать так, чтобы в левой части осталось только неизвестное в первой степени с коэффициентом равном единице.

Типы неравенств

Линейные неравенства: свойства и правила

Вспомним свойства числовых неравенств:

Если же а b и c > d, то а + c > b + d.

Если а 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.

Если а d, то а – c b, m — положительное число, то mа > mb и

Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).

Если же а > b, n — отрицательное число, то nа

Обе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.

Если а 0, то аc b, где а, b > 0, то а2 > b2, и если а b, где а, b > 0, то
b» height=»45″ src=»https://lh5.googleusercontent.com/MuRDPQeqxIZvVG_mHVaktFp6nlIEEbz8zdRs1ZW8CZbZacJrS4aKzrDyhKxXpJvc35TSAgiRpqr-63sGzL9_sPU80vFhR0ZDAmSmRFZtwEldDkWRttfSGuaJJIb7xWxZDugU3xTt»>

Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.

Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.

Свойства выше помогут нам использовать следующие правила.

Правила линейных неравенств

Решение линейных неравенств

Со школьных уроков мы помним, что у неравенств нет ярко выраженных различий, поэтому рассмотрим несколько определений.

Неравенства ax + b > 0 и ax > c равносильные, так как получены переносом слагаемого из одной части в другую.

Определение 3. Линейные неравенства с одной переменной x выглядят так:

где a и b — действительные числа. А на месте x может быть обычное число.

Равносильные преобразования

Рассмотрим пример: 0 * x + 5 > 0.

Как решаем:

Метод интервалов

Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.

Метод интервалов это:

Если a ≠ 0, тогда решением будет единственный корень — х₀;

Для этого найдем значения функции в точках на промежутке;

Как решаем:

Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.

Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.

По чертежу делаем вывод, что решение имеет вид (−∞, 4) или x

Графический способ

Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.

Алгоритм решения y = ax + b графическим способом

Рассмотрим пример: −5 * x − √3 > 0.

Как решаем

Ответ: (−∞, −√3 : 5) или x

Алгоритм решения линейного неравенства

a x b a x ≤ b a x > b a x ≥ b

Примеры решения линейных неравенств:

№1. Решить неравенство 3 ( 2 − x ) > 18.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )

№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6 x + 4 ≥ 3 x + 3 − 14

6 x − 3 x ≥ 3 − 14 − 4

x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).

Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).

№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

x + 6 − 9 x > − 8 x + 48

Квадратные неравенства

Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.

Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).

Алгоритм решения квадратного неравенства методом интервалов

Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.

Примеры решения квадратных неравенств:

№1. Решить неравенство x 2 ≥ x + 12.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3

x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0

Это значит, что знак на интервале, в котором лежит точка 6 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1

− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 0

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1

− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 0

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )

№4. Решить неравенство x 2 − 5 x 6.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1

x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0

Это значит, что знак на интервале, в котором лежит точка 10 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

№5. Решить неравенство x 2 4.

Решение:

Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.

( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2

x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0

Это значит, что знак на интервале, в котором лежит точка 3 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

№6. Решить неравенство x 2 + x ≥ 0.

Решение:

Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.

x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1

x 2 + x = 1 2 + 1 = 2 > 0

Это значит, что знак на интервале, в котором лежит точка 1 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )

Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.

Дробно рациональные неравенства

Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:

f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).

Примеры дробно рациональных неравенств:

x − 1 x + 3 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3

Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.

Алгоритм решения дробно рациональных неравенств:

f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.

Примеры решения дробно рациональных неравенств:

№1. Решить неравенство x − 1 x + 3 > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.

Это значит, что знак на интервале, в котором лежит точка 2 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )

№2. Решить неравенство 3 ( x + 8 ) ≤ 5.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

3 ( x + 8 ) − 5 \ x + 8 ≤ 0

3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 x − 40 x + 8 ≤ 0

x = − 37 5 = − 37 5 = − 7,4

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.

− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 0

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )

№3. Решить неравенство x 2 − 1 x > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.

x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.

Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )

Системы неравенств

Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.

Пример системы неравенств:

Алгоритм решения системы неравенств

Примеры решений систем неравенств:

№1. Решить систему неравенств < 2 x − 3 ≤ 5 7 − 3 x ≤ 1

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Точка 4 на графике жирная, так как знак неравенства нестрогий.

− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 0, знак неравенства после деления меняется на противоположный.

Графическая интерпретация решения:

Точка 2 на графике жирная, так как знак неравенства нестрогий.

№2. Решить систему неравенств < 2 x − 1 ≤ 5 1 − 3 x − 2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Точка 3 на графике жирная, так как знак неравенства нестрогий.

Графическая интерпретация решения:

№3. Решить систему неравенств < 3 x + 1 ≤ 2 x x − 7 >5 − x

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Графическая интерпретация решения:

Графическая интерпретация решения:

Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.

№4. Решить систему неравенств < x + 4 >0 2 x + 3 ≤ x 2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Графическая интерпретация решения первого неравенства:

Решаем методом интервалов.

D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16

x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1

Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.

Графическая интерпретация решения второго неравенства:

Источник

• ← Что значит найти множество делителей
• Что значит найти множество значений функции у тригонометрической функции →