Что значит наложение в геометрии

Наложения и движения

Напомним, что в нашем курсе геометрии равенство фигур определяется с помощью наложений. Мы говорим, что фигура Ф равна фигуре Фп если фигуру Ф можно совместить наложением с фигурой Ф₁. Понятие наложения в нашем курсе относится к основным понятиям геометрии, поэтому определение наложения не даётся. Под наложением фигуры Ф на фигуру Ф₁ мы понимаем некоторое отображение фигуры Ф на фигуру Ф₁ Более того, мы считаем, что при этом не только точки фигуры Ф, но и любая точка плоскости отображается в определённую точку плоскости, т. е. наложение — это отображение плоскости на себя.

Однако не всякое отображение плоскости на себя мы называем наложением. Наложения — это такие отображения плоскости на себя, которые обладают свойствами, выраженными в аксиомах (см. приложение 1, аксиомы 7—13). Эти аксиомы позволяют доказать все те свойства наложений, которые мы себе представляем наглядно и которыми пользуемся при доказательстве теорем и решении задач. Докажем, например, что при наложении различные точки отображаются в различные точки.

В самом деле, предположим, что это не так, т. е. при некотором наложении какие-то две точки А и В отображаются в одну и ту же точку С. Тогда фигура Ф₁, состоящая из точек А и В, равна фигуре Ф₂, состоящей из одной точки С. Отсюда следует, что Ф₂ = Ф₁ (аксиома 12), т. е. при некотором наложении фигура Ф₂ отображается в фигуру Ф₁. Но это невозможно, так как наложение — это отображение, а при любом отображении точке С ставится в соответствие только одна точка плоскости.

Из доказанного утверждения следует, что при наложении отрезок отображается на равный ему отрезок. Действительно, пусть при наложении концы А и В отрезка АВ отображаются в точки А₁ и В₁. Тогда отрезок АВ отображается на отрезок А₁В₁ (аксиома 7), и, следовательно, отрезок АВ равен отрезку А₁В₁. Так как равные отрезки имеют равные длины, то наложение является отображением плоскости на себя, сохраняющим расстояния, т. е. любое наложение является движением плоскости.

Источник

Наложения и движения

При наложении различные точки отображаются в различные точки.

Доказательство:

Из этого утверждения мы можем сделать вывод, что при наложении отрезок отображается на равный ему отрезок. Пусть при наложении концы А и В отрезка АВ отображаются в точки А₁ и В₁. Тогда отрезок АВ отображается на отрезок А₁В₁ (т.к. согласно аксиоме, если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки), и, следовательно, АВ=А₁В₁. Так как равные отрезки имеют равные длины, то наложение является отображением плоскости на себя, которое сохраняет расстояния, то есть любое наложение является движением плоскости.

Теорема

Доказательство

Дано: движение , АВС отображается в А₁В₁С₁, АВС=А₁В₁С₁

Доказать: движение — наложение

Доказательство:

Так как АВС=А₁В₁С₁ , то по определению существует наложение , при котором точки А, В и С отображаются в точки А₁, В₁ и С₁ соответственно. Докажем, что совпадает с .

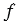
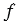
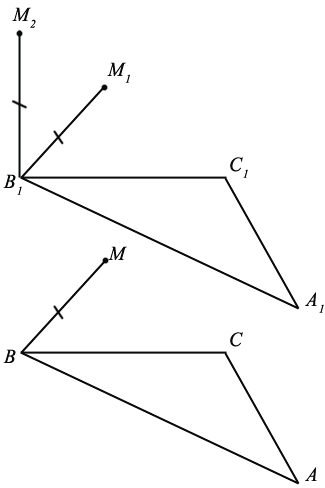
Предположим обратное. Тогда найдется хотя бы одна точка М, которая при движении отображается в точку М₁, а при наложении отображается в другую точку М₂. При отображениях и сохраняются расстояния, поэтому ВМ=В₁М₁, ВМ=В₁М₂, отсюда В₁М₁=В₂М₂, то есть точка В₁ равноудалена от точек М₁ и М₂.

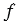
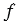
Аналогично можно доказать, что точки А₁ и С₁ равноудалены от точек М₁ и М₂. Следовательно, точки А₁, В₁, и С₁ лежат на серединном перпендикуляре к отрезку М₁М₂, но это не возможно, так как вершины А₁В₁С₁ не лежат на одной прямой. Значит, наше предположение неверно и отображение совпадает с , другими словами, движение является наложением. Теорема доказана.

Следствие

Поделись с друзьями в социальных сетях:

Источник

Что значит «Сравнить фигуры наложением»?

Вот, в учебниках по геометрии пишут, что фигуры (например отрезок) можно сравнивать путём наложения отрезков друг на друга. Но как это делать ни в одном не написано, нифига не понятно, что это означает.

Вот, я взял линейку, построил на листе два отрезка, и каким образом я буду их накладывать теперь друг на друга, чтобы узнать равны ли они? Мне, что, вырезать их надо будет, чтобы наложить друг на друга?

Площадь фигуры «круг обрезаный синусоидой»
Доброго времени суток уважаемые форумчане. Помогите решить задачку. Даже не задачку, Просто нужна.

Что значит «реактивная» и «активная» составляющие для ЭДС?
Здравствуйте. У меня в задании дана ЭДС 130 В / 50 Гц. Как определить её активную и реактивные.

Что значит «%d %d\n» в функции вывода в файл fprintf(f, «%d %d\n», i, j);
Что значит «%d %d\n» в функции вывода в файл fprintf(f, «%d %d\n», i, j); Запутался, объясните.

В учебниках или конкретно в. как его? Атанасяне?

Как не написано, должно быть определение. По идее, это вид движения (изометрического аффинного преобразования).

Бумага — это такое вещество из длинных молекул, которые состоят из атомов, находящихся в тепловом движении. Когда по бумаге проводят карандашом, на ней остаётся след — слои кристаллической решётки углерода. Молекулы воздуха стучатся об это хозяйство, что-то застревает, какие-то атомы, наоборот, улетают с поверхности. Циркуль — тоже конструкция из атомов; это кажется, что он полированный, а так он весьма себе бугристый. Кроме прочего, ещё и химические реации идут — окисление в атмосфере.

Вы по-прежнему думаете, что это имеет отношение к геометрическим абстракциям?

Источник

Сравнение отрезков

Одной из простейших геометрических фигур является отрезок. Для того чтобы сравнивать отрезки, можно использовать два способа:

Метод наложения:

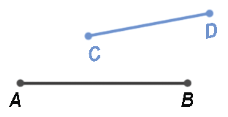
Пусть нам даны два отрезка AB и СD:

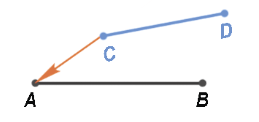
Совместим начало отрезка AB и СD (точки A и С).

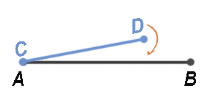
Затем повернем отрезок СD так, чтобы он совпал с отрезком AB.

Мы видим, что отрезок СD составляет часть отрезка AB, следовательно, мы можем сделать вывод, что отрезок AB больше отрезка СD.

Если точка делит отрезок на равные отрезки, то эту точку называют серединой отрезка.

Рассмотрим еще одну пару отрезков HG и ST.

Совместим начало отрезка HG и ST.

Затем повернем отрезок ST так, чтобы он совпал с отрезком HG.

В данном случае мы видим, что совпали не только точки S и H (начала отрезков HG и ST), но и точки G и T (концы отрезков HG и ST), то есть отрезки совпадают, а нам известно, что две геометрические фигуры называются равными, если их можно совместить наложением.

Вывод:

Измерение длин:

Для измерения отрезков, необходимо наложить на него единичные отрезки, и длиннее будет считаться тот отрезок, которому соответствует большее число единичных отрезков.

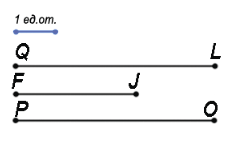
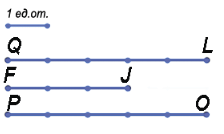
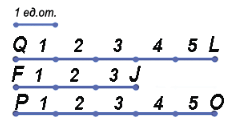
Пример: Пусть у нас есть единичный отрезок. Рассмотрим три отрезка QL, FJ и PO.

Наложим единичный отрезок на данные.

Посчитаем, какое количество единичных отрезков накладывается на каждый из отрезков, получаем: QL = 5 ед.от., FJ = 3 ед.от., PO = 5 ед. от.

Поделись с друзьями в социальных сетях:

Источник

«Наложение» в геометрии. Что это? Как объяснить?

Объясните, что такое наложение (в геометрии).

Наложение основано на аксиоме, утверждающей, что любые фигуры на плоскости можно передвигать, не меняя их вида и характеристик.

Процесс наложения одной фигуры на другую происходит путём передвижения плоскостей. При этом, плоскости могут и переворачиваться.

Фигуры будут равными, если их плоскости совпадут при наложении друг на друга.

Наложение можно проводить как в реальности, например взять два картонных кружочка и накладывать один на другой, так и в виртуальности, когда например на компьютере есть макеты этих фигур и там они также накладываются между собой.

С помощью наложения можно выяснить равны ли фигуры, все ли линии совпадают, есть или нет каких-то выпуклостей, которые присутствуют только на одной фигуре и т.д.

Более подробно смотрите здесь:

Под наложением подразумевают прием теоремных доказательств, когда передвигают и переворачивание фигуры по плоскости. Если все точки фигуры при этом совпадают, они считаются равными. Поверхность используется плоская и кривая. Тогда должны совпадать все складочки и разрывы.

Наложением могут сравниваться между собой две фигуры (геометрические). Для этого их (не меняя масштаба, но можно переворачивать) просто накладывают друг на друга. Это делается как непосредственно, так и приводя (с помощью компьютера) к какой-то единой фигуре.

Источник