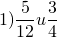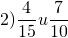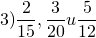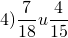Что значит наименьший общий знаменатель

Общий знаменатель, понятие и определение.

Так для чего нужен общий знаменатель, или когда нужен общий знаменатель?
Ответ довольно прост, мы имеем право дроби складывать и вычитать только когда у данных дробей есть общий знаменатель. Поэтому важно понять, как находить общий знаменатель.

Определение:
Общий знаменатель – это число всегда положительное на которое делятся знаменатели данных дробей.

Формула основного свойства рациональных чисел.

Такое решение называется приведением к общему знаменателю. Мы имеем право умножать одновременно на одно и тоже число и числитель и знаменатель.

Наименьший общий знаменатель.

Что такое наименьший общий знаменатель?

Определение:
Наименьший общий знаменатель – это наименьшее положительное число кратное знаменателям данных дробей.

Как привести к наименьшему общему знаменателю? Чтобы ответить на этот вопрос рассмотрим пример:

Решение:
Чтобы найти наименьший общий знаменатель нужно найти наименьшее общее кратное (НОК) знаменателей этих дробей.

У первой дроби знаменатель равен 20 разложим его на простые множители.
20=2⋅5⋅2

Так же разложим и второй знаменатель дроби 14 на простые множители.
14=7⋅2

Ответ: наименьший общий знаменатель будет равен 140.

Как привести дробь к общему знаменателю?

Нужно первую дробь \(\frac<1><20>\) домножить на 7, чтобы получить знаменатель 140.

Правила или алгоритм приведения дробей к общему знаменателю.

Алгоритм приведения дробей к наименьшему общему знаменателю:

Общий знаменатель для нескольких дробей.

Как найти общий знаменатель для нескольких дробей?

Рассмотрим пример:
Найдите наименьший общий знаменатель для дробей \(\frac<2><11>, \frac<1><15>, \frac<3><22>\)

Решение:
Разложим знаменатели 11, 15 и 22 на простые множители.

Число 11 оно само по себе уже простое число, поэтому его расписывать не нужно.
Разложим число 15=5⋅3
Разложим число 22=11⋅2

Найдем наименьшее общее кратное (НОК) знаменателей 11, 15, и 22.
НОК(11, 15, 22)=11⋅2⋅5⋅3=330

Мы нашли наименьший общий знаменатель для данных дробей. Теперь приведем данные дроби \(\frac<2><11>, \frac<1><15>, \frac<3><22>\) к общему знаменатели равному 330.

Вопросы по теме:
Какой общий знаменатель у дробей \(\bf \frac<2><25>\) и \(\bf \frac<1><14>\)?
Ответ:
Какой наименьший общий знаменатель у дробей 14 и 25? Воспользуемся алгоритмом приведения дробей к общему знаменателю алгебраических дробей.

Сначала разложим на простые множители знаменатели 14 и 25.
14=2⋅7
25=5⋅5
Теперь найдем НОК(14,25)=2⋅7⋅5⋅5=350.

Это мы нашли наименьший общий знаменатель:

Но не всегда нужно находит наименьший общий знаменатель иногда, можно найти любой знаменатель, а потом можно конечную дробь сократить. Например, для дробей \(\frac<2><25>\) и \(\frac<1><14>\) знаменателем может быть число 700, 1400 и т.д.

Источник

Приведение дроби к наименьшему общему знаменателю: правило, примеры решений

В данной статье рассказывается, как привести дроби к общему знаменателю и как найти наименьший общий знаменатель. Приведены определения, дано правило приведения дробей к общему знаменателю и рассмотрены практические примеры.

Что такое приведение дроби к общему знаменателю?

Если же дроби имеют разные знаменатели, то их всегда можно привести к общему знаменателю при помощи нехитрых действий. Чтобы сделать это, нужно числитель и знаменатель умножить на определенные дополнительные множители.

Приведение дробей к общему знаменателю

Общий знаменатель: определение, примеры

Что такое общий знаменатель?

Другими словами, общим знаменателем какого-то набора дробей будет такое натуральное число, которое без остатка делится на все знаменатели этих дробей.

Ряд натуральных чисел бесконечен, и поэтому, согласно определению, каждый набор обыкновенных дробей имеет бесконечное множество общих знаменателей. Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.

Пример 1. Общий знаменатель

Значит, 150 не является общим знаменателем указанных дробей.

Наименьший общий знаменатель

Наименьшее натуральное число из множества общих знаменателей какого-то набора дробей называется наименьшим общим знаменателем.

Наименьший общий знаменатель

Как найти наименьший общий знаменатель? Его нахождение сводится к нахождению наименьшего общего кратного дробей. Обратимся к примеру:

Пример 2. Найти наименьший общий знаменатель

Как привести дроби к наименьшему общему знаменателю

Существует правило, которое объясняет, как привести дроби к общему знаменателю. Правило состоит из трех пунктов.

Правило приведения дробей к общему знаменателю

Рассмотрим применение этого правила на конкретном примере.

Пример 3. Приведение дробей к общему знаменателю

По правилу, сначала найдем НОК знаменателей дробей.

Умножаем числитель и знаменатель дробей на дополнительные множители и получаем:

Приведение нескольких дробей к наименьшему общему знаменателю

По рассмотренному правилу к общему знаменателю можно приводить не только пары дробей, но и большее их количество.

Приведем еще один пример.

Пример 4. Приведение дробей к общему знаменателю

Вычислим НОК знаменателей. Находим НОК трех и большего количества чисел:

Далее вычислим дополнительные множители для каждой дроби.

Умножаем дроби на дополнительные множители и переходим к наименьшему общему знаменателю:

3 2 · 36 = 108 72 5 6 · 12 = 60 72 3 8 · 9 = 27 72 17 18 · 4 = 68 72

Источник

Как найти наименьший общий знаменатель

Приведем пример нахождения наименьшего общего знаменателя трех дробей: 4/5, 7/8, 11/14. Для начала разложим знаменатели 5, 8, 14 на множители: 5 = 1 * 5, 8 = 2 * 2 * 2 = 2^3, 14 = 2 * 7. Далее вычисляем НОК (5, 8, 14), перемножая все числа, входящие хотя бы в одно из разложений. НОК (5, 8, 14) = 5 * 2^3 * 7 = 280. Заметим, что если множитель встречается в разложении нескольких чисел (множитель 2 в разложении знаменателей 8 и 14), то берем множитель в большей степени (2^3 в нашем случае).

Итак, наименьший общий знаменатель дробей получен. Он равен 280 = 5 * 56 = 8 * 35 = 14 * 20. Здесь мы получаем числа, на которые надо умножить дроби с соответствующими знаменателями, чтобы привести их к наименьшему общему знаменателю. Получаем 4/5 = 56 * (4/5) = 224 / 280, 7/8 = 35 * (7/8) = 245/280, 11/14 = 20 * (11/14) = 220/280.

Приведение к наименьшему общему знаменателю алгебраических дробей выполняется по аналогии с арифметическими дробями. Для наглядности рассмотрим задачу на примере. Пусть даны две дроби (2 * x) / (9 * y^2 + 6 * y + 1) и (x^2 + 1) / (3 * y^2 + 4 * y + 1). Разложим на множители оба знаменателя. Заметим, что знаменатель первой дроби представляет собой полный квадрат: 9 * y^2 + 6 * y + 1 = (3 * y + 1)^2. Для разложения второго знаменателя на множители необходимо применить метод группировки: 3 * y^2 + 4 * y + 1 = (3 * y + 1) * y + 3 * y + 1 = (3 * y + 1) * (y + 1).

Таким образом наименьший общий знаменатель равен (y + 1) * (3 * y + 1)^2. Умножаем первую дробь на многочлен y + 1, а вторую дробь на многочлен 3 * y + 1. Получаем дроби, приведенные к наименьшему общему знаменателю:

2 * x * (y + 1) / (y + 1) * (3 * y + 1)^2 и (x^2 + 1) * (3 * y + 1) / (y + 1) * (3 * y + 1)^2.

Источник

Наименьший общий знаменатель (НОЗ) алгебраических дробей, его нахождение.

Для сложения и вычитания алгебраических дробей их предварительно нужно привести к такому виду, чтобы они имели одинаковые знаменатели. Другими словами, они приводятся к общему знаменателю. В этой статье мы сначала дадим определение общего знаменателя и наименьшего общего знаменателя (НОЗ) алгебраических дробей. А дальше подробно остановимся на нахождении наименьшего общего знаменателя: разберем соответствующий алгоритм и рассмотрим решения примеров.

Навигация по странице.

Что называют общим знаменателем алгебраических дробей?

Похожим образом определяется и общий знаменатель алгебраических дробей. Отличие состоит лишь в том, что вместо чисел, которые составляют обыкновенную дробь, речь уже идет о многочленах, так как именно они стоят в числителе и знаменателе алгебраической дроби.

Общим знаменателем алгебраических дробей называется многочлен, который делится на знаменатель любой из дробей.

Сразу стоит отметить, что мы будем работать с общими знаменателями алгебраических дробей, представленными преимущественно в виде произведения, а не в виде многочлена стандартного вида. Это связано с особенностями нахождения общего знаменателя алгебраических дробей (о которых мы будем говорить в этой статье чуть позже).

Наименьший общий знаменатель (НОЗ)

На практике обычно используют общий знаменатель алгебраических дробей, который среди всего их множества имеет самый простой вид. При этом можно слышать, что говорят о наименьшем общем знаменателе.

Наименьший общий знаменатель (НОЗ) алгебраических дробей – это их общий знаменатель самого простого вида.

Сразу заметим, что термин «наименьший общий знаменатель» по отношению к алгебраическим дробям не является общепризнанным, и лучше говорить просто об общем знаменателе. Этому есть объяснение.

Основная проблема состоит в том, что фраза «самого простого вида» в приведенном определении является не совсем конкретной. Основной вкладываемый в нее смысл таков: любой другой общий знаменатель данных алгебраических дробей должен без остатка делиться на общий знаменатель самого простого вида. А неконкретность заключается в том, что можно использовать различные числовые коэффициенты в произведении, являющимся общим знаменателем дробей. Поясним эти моменты на примере.

Алгоритм отыскания общего знаменателя алгебраических дробей, примеры

Теперь поставим перед собой задачу: пусть даны несколько алгебраических дробей и требуется найти их общий знаменатель. Для ее решения будем использовать следующий алгоритм отыскания общего знаменателя алгебраических дробей:

Составленное таким способом произведение будет искомым общим знаменателем алгебраических дробей.

Несомненно, можно просто составить произведение, взяв в качестве множителей все знаменатели исходных алгебраических дробей. Но использование такого общего знаменателя в подавляющем большинстве случаев нерационально, и он часто по смыслу далек от НОЗ.

Все тонкости применения записанного алгоритма (которых, как Вы убедитесь, немало) разберем при решении примеров.

Определите общий знаменатель дробей и .

Знаменатели заданных алгебраических дробей не нуждаются в разложении на множители. Для определения общего знаменателя воспользуемся изученным алгоритмом.

Теперь перейдем к случаям, когда знаменатели алгебраических дробей имеют целые числовые множители. При нахождении их общего знаменателя следует придерживаться приведенного алгоритма, а целые числовые множители разложить на простые множители.

Найдите общий знаменатель дробей и .

После разложения чисел в знаменателях дробей на простые множители, они примут вид и . Теперь можно приступать к составлению общего знаменателя.

Если внимательно посмотреть на результаты двух разобранных примеров, то можно заметить, что общие знаменатели дробей содержат все множители, присутствующие в разложениях знаменателей, причем если некоторый множитель имеется в нескольких знаменателях, то он берется с наибольшим из имеющихся показателей степени. А если в знаменателях имеются целые коэффициенты, то в общем знаменателе присутствует числовой множитель, равный наименьшему общему кратному этих числовых коэффициентов.

Предыдущие рассуждения позволяют записать еще один алгоритм отыскания общего множителя алгебраических дробей:

Можно использовать как первый, так и второй алгоритм, в зависимости от того, какой кажется более удобным.

Обговорим еще пару нюансов.

Иногда общие множители в знаменателях дробей могут быть «спрятаны» за числовыми коэффициентами. Поэтому имеет смысл вынести за скобки числовые коэффициенты при старших степенях переменных в каждом из множителей, находящихся в знаменателях.

Какой общий знаменатель имеют дроби и .

Наконец, если исходные дроби имеют дробные коэффициенты, то перед нахождением их общего знаменателя обычно избавляются от дробных коэффициентов, выполнив умножение числителя и знаменателя дробей на некоторое число. Подобное действие мы уже выполняли, когда говорили о преобразовании алгебраических дробей.

Упростите алгебраические дроби и , после чего определите их общий знаменатель.

В заключение этой статьи хочется лишь сказать, что часто не так сложно составить общий знаменатель алгебраических дробей, как выполнить предварительное разложение знаменателей этих дробей на множители.

Источник

Общий знаменатель дробей

Это правило позволяет легко и быстро устно найти наименьший общий знаменатель дробей.

Правило нахождения наименьшего общего знаменателя для двух или нескольких дробей:

1) Выбираем из всех знаменателей наибольшее число и проверяем, делится ли оно на остальные. Если делится, то это число и есть наименьший общий знаменатель (НОЗ) этих дробей.

2) Если наибольший знаменатель не делится на все остальные, умножаем его на 2 и проверяем, делится ли полученное число на все остальные. Если делится, то это новое число и есть НОЗ.

3) Если после умножения на два новое число не делится на все остальные, наибольший из знаменателей умножаем на 3,4,5 и так далее до тех пор, пока новое число не будет делиться на все остальные. Это новое число и есть наименьший общий знаменатель.

Найти общий знаменатель дробей:

Выбираем бОльший знаменатель и проверяем, делится ли он на меньший. 12 на 4 делится. Значит, наименьший общий знаменатель этих дробей равен 12.

Выбираем больший знаменатель и проверяем, делится ли он на меньший. 15 на 10 не делится. Умножаем бОльший знаменатель на 2 и проверяем, делится ли новое число на меньший знаменатель. 15∙2=30, 30 на 10 делится. Значит, наименьший общий знаменатель этих дробей равен 30.

Выбираем большее число и проверяем, делится ли оно на остальные. 20 на 15 и 12 не делится. Большее число умножаем на 2 и проверяем, делится ли новое число на остальные. 20∙2=40. 40 на 15 и 12 не делится. Значит, большее число 20 надо умножить на 3 и проверить, будет ли делиться результат на остальные. 20∙3=60. 60 делится и на 15, и на 12. Поэтому 60 — наименьший общий знаменатель этих дробей.

Большее — 18. Оно не делится на меньшее — 15. Умножаем большее на 2: 18∙2=36. 36 на 15 не делится. Умножаем большее на 3: 18 ∙3=54. 54 на 15 не делится. Умножаем большее на 4: 18∙4=72. 72 на 15 не делится. Умножаем большее на 5: 18∙5=90. 90 на 15 делится. Значит, наименьший общий знаменатель этих дробей равен 90.

В следующий раз мы посмотрим, как это правило применять при сложении и вычитании дробей с разными знаменателями.

Источник