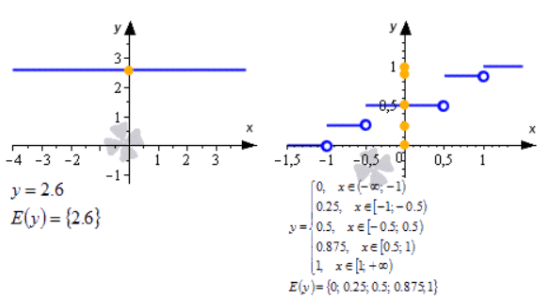
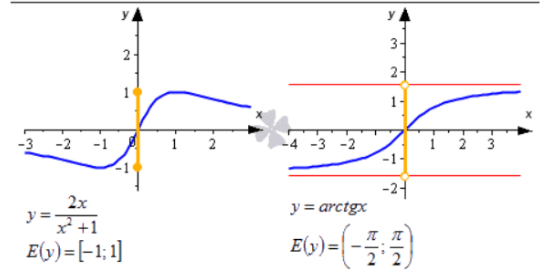
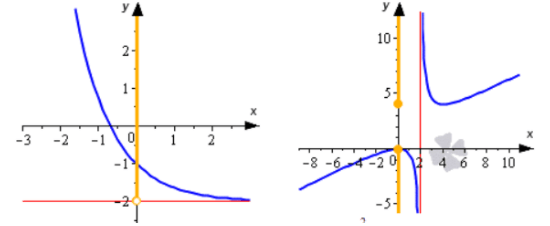
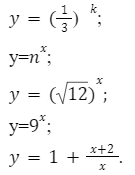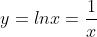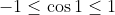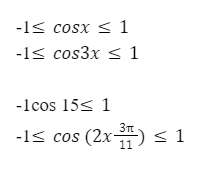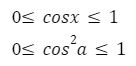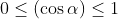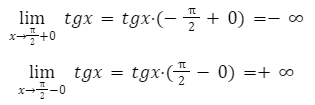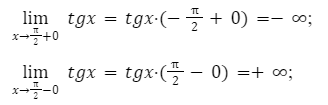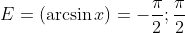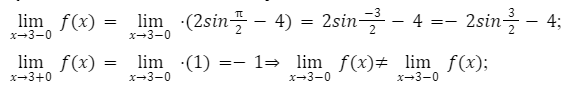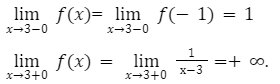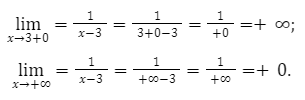Что значит функция принимает положительные значения
Как решать задачи на квадратичную функцию
В предыдущем уроке мы подробно разобрали, как построить параболу. В этом уроке мы разберем, как решать типовые задачи на квадратичную функцию.
Как найти нули квадратичной функции
Подставим в исходную функцию вместо « y » ноль и решим полученное квадратное уравнение.
0 = x 2 − 3
x 2 − 3 = 0
x1;2 =
| 0 ± √ 0 2 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
| ± √ 12 |
| 2 |
x1;2 =
| ± √ 4 · 3 |
| 2 |
x1;2 =
| ± 2√ 3 |
| 2 |
x1;2 = ±√ 3
| x1 = √ 3 | x2 = − √ 3 |
Как найти при каких значениях « x » квадратичная функция принимает заданное числовое значение
Чтобы найти при каких значениях « x » квадратичная функция принимает заданное числовое значение, нужно:
При каких значениях « x » функция принимает значение « −3 ».
Подставим в исходную функцию вместо « y = −3 » и найдем « x ».
−3 = x 2 − x − 3
x 2 − x − 3 = −3
x 2 − x − 3 + 3 = 0
x 2 − x = 0
x1;2 =
| 1 ± √ 1 2 − 4 · 1 · 0 |
| 2 · 1 |
x1;2 =
| 1 ± √ 1 |
| 2 |
x1;2 =
| 1 ± 1 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 1 | x2 = 0 |
Как найти координаты точек пересечения параболы и прямой
Чтобы найти точки пересечения параболы с прямой нужно:
Найти координаты точек пересечения параболы « y = x 2 » и прямой « y = 3 − 2x ».
Приравняем правые части функций и решим полученное уравнение относительно « x ».
x 2 = 3 − 2x
x 2 − 3 + 2x = 0
x 2 + 2x − 3 = 0
x1;2 =
| 2 ± √ 2 2 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
| 2 ± √ 4 + 12 |
| 2 |
x1;2 =
| 2 ± √ 16 |
| 2 |
x1;2 =
| 2 ± 4 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 3 | x2 = −1 |
Теперь подставим в любую из заданных функций (например, в полученные числовые значения « x », чтобы найти координаты « y » точек пересечения.
1) x = 3
y = 3 − 2x
y(3) = 3 − 2 · 3 = 3 − 6 = −3
(·) A (3; −3) — первая точка пересечения.
2) x = −1
y = 3 − 2x
y(−1) = 3 − 2 · (−1) = 3 + 2 = 5
(·) B (−1; 5) — вторая точка пересечения.
Запишем полученные точки пересечения с их координатами в ответ.
Как определить, принадлежит ли точка графику функции параболы
Чтобы проверить принадлежность точки параболе нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси « Ox » вместо « x », а координату по оси « Oy » вместо « y ») и выполнить арифметические расчеты.
Как найти точки пересечения параболы с осями координат
Найти координаты точек пересечения параболы с осями координат.
Сначала определим точки пересечения функции с осью « Ox ». На графике функции эти точки выглядят так:
Как видно на рисунке выше, координата « y » точек пересечения с осью « Ox » равна нулю, поэтому подставим « y = 0 » в исходную функцию « y = x 2 −3x + 2 » и найдем их координаты по оси « Ox ».
0 = x 2 −3x + 2
x 2 −3x + 2 = 0
x1;2 =
| 3 ± √ 3 2 − 4 · 1 · 2 |
| 2 · 1 |
x1;2 =
| 3 ± √ 9 − 8 |
| 2 |
x1;2 =
| 3 ± √ 1 |
| 2 |
x1;2 =
| 3 ± 1 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 2 | x2 = 1 |
Теперь найдем координаты точки пересечения с осью « Oy ».
Как видно на рисунке выше, координата « x » точки пересечения с осью « Oy » равна нулю.
Подставим « x = 0 » в исходную функцию « y = x 2 −3x + 2 » и найдем координату точки по оси « Oy ».
y(0) = 0 2 − 3 · 0 + 2 = 2
Выпишем координаты полученной точки: (·) C (0; 2)
Запишем в ответ все координаты точек пересечения параболы с осями.
Как определить при каких значениях x функция принимает положительные или отрицательные значения
Чтобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно:
С помощью графика квадратичной функции, изображенного на рисунке, ответить: При каких значениях « x » функция принимает 1) положительные значения; значения.
Проведем через точки, где график функции пересекает ось « Ox » прямые.
Определим области, где функция принимает отрицательные или положительные значения.
Подпишем над каждой полученной областью, какие значения принимает « x » в каждой из выделенных областей.
Ответ: при « x » и « x > 2 » функция принимает отрицательные значения; при функция принимает положительные значения.
Как найти нули функции?
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
График функции у=k/x выглядит следующим образом: 
Рассмотрим примеры нахождения нулей функции. Пример №1. Найти нули функции (если они существуют):
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0.
Значит, нули функции это числа (-76) и 95.
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Метод интервалов: примеры, решения
Метод интервалов принято считать универсальным для решения неравенств. Иногда этот метод также называют методом промежутков. Применим он как для решения рациональных неравенств с одной переменной, так и для неравенств других видов. В нашем материале мы постарались уделить внимание всем аспектам вопроса.
Что ждет вас в данном разделе? Мы разберем метод промежутков и рассмотрим алгоритмы решения неравенств с его помощью. Затронем теоретические аспекты, на которых основано применение метода.
Особое внимание мы уделяем нюансам темы, которые обычно не затрагиваются в рамках школьной программы. Например, рассмотрим правила расстановки знаков на интервалах и сам метод интервалов в общем виде без его привязки к рациональным неравенствам.
Алгоритм
Кто помнит, как происходит знакомство с методом промежутков в школьном курсе алгебры? Обычно все начинается с решения неравенств вида f(x) или ≥). Здесь f(x) может быть многочленом или отношением многочленов. Многочлен, в свою очередь, может быть представлен как:
произведение линейных двучленов с коэффициентом 1 при переменной х;
произведение квадратных трехчленов со старшим коэффициентом 1 и с отрицательным дискриминантом их корней.
Приведем несколько примеров таких неравенств:
Запишем алгоритм решения неравенств такого вида, как мы привели в примерах, методом промежутков:
Четреж, с которым мы будем работать, может иметь схематический вид. Излишние подробности могут перегружать рисунок и затруднять решение. Нас будет мало интересовать маштаб. Достаточно будет придерживаться правильного расположения точек по мере роста значений их координат.
При работе со строгими неравенствами мы будем использовать обозначение точки в виде круга с незакрашенным (пустым) центром. В случае нестрогих неравенств точки, которые соответствуют нулям знаменателя, мы будем изображать пустыми, а все остальные обычными черными.
Отмеченные точки разбивают координатную прямую на несколько числовых промежутков. Это позволяет нам получить геометрическое представление числового множества, которое фактически является решением данного неравенства.
Научные основы метода промежутков
Основан подход, положенный в основу метода промежутков, основан на следующем свойстве непрерывной функции: функция сохраняет постоянный знак на интервале (a, b), на котором эта функция непрерывна и не обращается в нуль. Это же свойство характерно для числовых лучей (−∞, a) и (a, +∞).
Приведенное свойство функции подтверждается теоремой Больцано-Коши, которая приведена во многих пособиях для подготовки к вступительным испытаниям.
Возьмем любой из промежутков и покажем на нем, что на всем промежутке выражение из левой части неравенства будет иметь постоянный знак. Пусть это будет промежуток (−∞, −1). Возьмем любое число t из этого промежутка. Оно будет удовлетворять условиям t
Область значений функции
Время чтения: 40 минут
Область значений функции, ее свойства и примеры решения
В данном материалы мы подробно рассмотрим значение функции. Определим основные методы ее вычисления. Изучим множество значений функции.
Подробно, разберем на примерах, методы нахождения функции. Прежде, чем начать изучение материала, охарактеризуем основное определение значению функции.
Функции удобно изображать в виде графических прямых или кривых.
Понятие области определения функции
Функция задается тогда, когда любому значению, например x соответствует любое значение y. Независимой переменной называют значение х или по другому аргументом. Числовое значение y, как правило является зависимой переменной.
Данная зависимость между x и y в алгебре называют функциональной. Записывают ее в виде функции y = f(x)
Другими словами, функция, это когда значения одной переменной зависят от значений другой переменной.
Далее можно сформулировать определение область функции. То есть, на какой промежуток действе функции распространяется.
Область функции можно выразить геометрически. Например, в виде графика. Где за основу берутся оси х и y.
Например:
Область значений функции y = z 2 — это все значения, которые будут больше либо равные нулю. В виде записи это выглядит следующим образом: f(у): у ≥ 0. Не все функции обозначаются одинаковыми формулировками, в основном D(f). Но тригонометрические функции обозначаются немного иначе. D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус. Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = x. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1]. Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Для указания множества чисел в определенном промежутке, необходимо выполнить следующие действия:
Если у промежутка нет правой границы, записываем знак бесконечности или плюс бесконечности. Если отсутствует левая граница, записываем знак минус бесконечности.
В случае, если записывается множество, которое состоит из нескольких промежутков, ставится знак объединение.
Рассмотрим на примерах
Все действительные числа от 1 до 9, можно выразить в следующей записи. [1;9]
Все положительные числовые значения, имеют следующий вид: (0; +);
Так как ноль, не является положительным число, то возле него ставится круглая скобка.
Область значения и определения функции
Чаще всего область определения выражают как функцию D(y).
В математике существует две главных запрещенных (недопустимых) операции:
При определении области функции, вступают в силу два основных ограничения:
Область определения постоянной функции
Постоянная функция записывается обычной формулой y = N, а именно f(x) = N, где N — любое действительное число. Иными словами, принято называть константа.
Постоянная функция — это функция, при которой всегда наблюдается одно и то же числовое значение, независимо от того какое числовое значения имеет аргумент.
Область определения степенной функции
Область определения степенной функции, всегда имеет непосредственную зависимость, от значений показателя степени.
Рассмотрим основные моменты:
Если k — неотрицательное целое число, то областью определения данной функции является множество любых, обязательно, действительных чисел: (-∞, +∞).
Когда степенной показатель, является не целое число, то функция имеет следующий вид D(f) = [0, +∞).
Когда k — отрицательное целое число, то область определения функции представляет собой (-∞, 0) ∪ (0, +∞).
Для остальных действительных отрицательных, a область определения степенной функции — числовой промежуток (0, +∞).
Если k равно нулю, то функция определена для всех чисел, кроме нуля. Так как ноль нельзя возвести в степень, а любое другое число в нулевой степени равно 1.
То есть, при k = 0, y =x0 = 1, на заданной области определения (-∞, 0) ∪ (0, +∞).
Область определения показательной функции
Показательная функция записывается как: y=k x
где значение x — показатель степени;
k — число, которое обязательно больше нуля и не равно единице.
Область определения показательной функции — это множество значений R.
Основные примеры показательных функций:
Область определения, для этих функций, записывается следующим образом: (−∞, +∞).
Область определения логарифмической функции
Логарифмическая функция выражается как: y=log n k
Рассмотрим на примере, характер решения задачи данной функции.
Пример №1
y=ln x, определить область определения натурального логарифма. D(y)=(0;+).
На заданном интервале, производная будет иметь положительное значение, и функция будет возрастать на всем промежутке.
Определим односторонний предел при, стремлении аргумента к нулю и когда значение x стремится к бесконечности.
Из данного решения мы видим, что значения будут возрастать от минус бесконечности до плюс бесконечности.
Из этого следует, что множество всех действительных чисел – является областью значений функции натурального логарифма ln.
Ответ: множество всех действительных чисел, это и есть область значений функции ln.
Область определения и множество значений функций косинус, синус, тангенс, котангенс
Множество значений всех действительных чисел, будет являться областью определения функций синус и косинус, и записываться следующим образом.
Функции являются ограниченными, как сверху, так и снизу.
y = sin x и y = cos x
Промежуток их действия сводится к неравенству -1 ≤ y ≤ 1
Областью определения функции тангенс tg x, является выражение 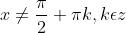
Областью определения функции y = сtg x является множество чисел 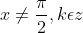
На нижеприведенных примерах подробно расписано решение задач, при определении области функции, при заданных промежутках значений.
Пример №1
Определить область значения функции sin x
Данный вид функции относится к категории периодической. Ее период равняется 2π
Определяем множество значений на следующем отрезке: (0;2π).
Пример №2
Необходимо определить область значения функции cos x.
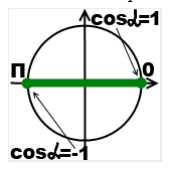
Наименьшее значение равно -1;
Минимальное значение косинуса равняется -1, потому что наименьшее значение х, на окружности стремится к этому значению и, следовательно, равняется -1.
Максимальное значение косинуса будет соответственно 1. Поскольку значение на окружности х имеет число 1.
Область значение, следовательно, будет от минус одно до плюс одного. [-1;1].
Применяем двойное неравенство и записывает следующее выражение:
Область значения косинуса никогда не зависит от аргумента, только если сам аргумент выражен в виде сложного выражения. Где имеют место ограничения касающиеся области определения и области значения.
Таким образом, минимальное значение cos x, cos (15α), cos(5-11x) и так далее, будет однозначно равняться -1;
Самым максимальным значением cos x, cos(4φ), cos(5х+3) равняется 1.
Область значений функции y=cos x — также промежуток [-1;1].
Область значения квадрата косинуса, будет промежуток от нуля до единицы [0;1]. Потому что число в четной степени, является не отрицательным.
Аналогичным образом находим область значений модуля косинуса — промежуток [0;1]
Пример №3
y = tgx на определенном интервале 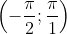
Решение:
Из правил алгебры, известно, что производная тангенса имеет положительное значение. Соответственно функция будет иметь возрастающую характеристику.
Далее необходимо определить поведение функции, в заданных пределах.
Выполнив решение, мы получаем рост значений от минус до плюс бесконечности. Решение будет сводится к следующему: множество решение заданной функции, будет множество всех действий функции.
Пример №4
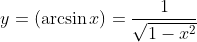
Решение:
Для всех значений x производная будет положительной, в пределах от -1;1
Следовательно, область значения арксинуса равняется:
Пример №5
Разберем функцию 2sinx2-4, где значение х меньше либо равно значению 3. Необходимо вычислить область значений.
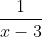
Функция является для всех значений x определенной.
Наблюдаем недопустимый вид при значении аргумента − 3.
При приближении к данному аргументу функция стремится к 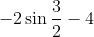
Наблюдается разрыв в точке 3. Когда функция стремится к данному разрыву ее числовые значения приближаются к -1. Минус бесконечность будет наблюдаться при стремлении к такой точке, но только с правой стороны.
Из этого следует вся область значений данной функции разбивается на три интервала. (-;−3], (−3 ;3], (3;+)(-;-3], (-3; 3], (3;+).
Первый интервал имеет функцию, следующего вида 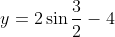
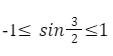
На промежутке -∞;-3, функция имеет следующие значения [-6;-2].
Функция y=-1, получается на полуинтервале (−3;3]. Следовательно, все значения будут сводится на данном интервале к одному числу, а именно -1.
Проанализируем второй промежуток (3;-+∞). Так как функция 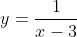

Если значение x больше значения 3, то большинство множеств функции будет в промежутке от нуля до +∞.