Что значит фигурная скобка в функции
Скобки в математике
Вы будете перенаправлены на Автор24
Скобки в математике играют очень важную роль: с помощью них задаётся порядок действий с выражением, обозначаются границы промежутков и необходимость выполнения какого-либо действия над выражением. Также с помощью скобок обозначаются вектора и матрицы и действия с множествами.
Использование круглых скобок в математике
Круглые скобки в математике встречаются наиболее часто, и они используются для множества целей.
Первое применение.
С помощью круглых скобок устанавливается порядок действий для вычисления алгебраического выражения. Выражение, которое стоит в скобках, вычисляется первым, за ним следует вычисление всех остальных.
В случае же если в выражении скобок много и одна находится внутри другой — первыми вычисляются скобки с максимальной глубиной вложенности.
Второе применение.
Третье применение.
Круглые скобки также используются для обозначения действий, которые необходимо совершить над всем выражением, стоящим в скобках. Под действием здесь имеются в виду возведение в степень, взятие производной или вычисление подинтегрального выражения.
$(x+2)^2; \int_1^5 (x^2+5x)dx; f’(x)= (5x^2 + 1)’$
Четвёртое применение.
Пятое применение.
Готовые работы на аналогичную тему
Пятое применение.
Квадратные скобки в математике
Что же означают квадратные скобки в математике и для чего они используются?
Квадратные скобки в математике встречаются реже чем круглые, но всё же их можно встретить довольно часто.
Первое применение.
Квадратные скобки иногда используются при записи выражений наряду с круглыми для того, чтобы было проще различить скобки и, соответственно, задаваемый ими порядок действий. Часто с такой целью квадратные скобки используются для записи формул физики и других технических наук.
Второе применение.
Третье применение.
С помощью квадратной скобки записывают совокупности. Совокупности — это системы уравнений, для которых справедливы все множества решений для каждого уравнения, входящего в совокупность.
$\left [ \begin
Фигурная скобка в математике
Первое применение.
С помощью символа фигурной скобки обозначают систему уравнений, решением которой являются корни, подходящие для всех уравнений, включённых в систему.
Второе применение.
Третье применение.
Треугольные скобки
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 06 03 2021
Зачем нужны фигурные скобки «< >» в обозначении промежутков
Фигурные скобки используются в математике для обозначения операции взятия дробной части; приоритета операций, как третий уровень вложенности (после круглых и квадратных скобок); для обозначения множеств.
Фигурные скобки используются в математике для обозначения операции взятия дробной части; приоритета операций, как третий уровень вложенности (после круглых и квадратных скобок); для обозначения множеств.
Скобки для указания порядка выполнения действий
Основное предназначение скобок – указание порядка выполняемых действий. Тогда выражение может иметь одну или несколько пар круглых скобок. По правилу всегда выполняется первым действие в скобках, после чего умножение и деление, а позже сложение и вычитание.
Рассмотрим на примере заданное выражение. Если дан пример вида 5+3-2, тогда очевидно, что действия выполняются последовательно. Когда это же выражение записывается со скобками, тогда их последовательность меняется. То есть при (5+3)-2 первое действие выполняется в скобках. В данном случае изменений не будет. Если выражение будет записано в виде 5+(3-2), тогда в начале производятся вычисления в скобках, после чего сложение с числом 5. На исходное значение в этом случае оно не повлияет.
Рассмотрим пример, который покажет, как при изменении положения скобок может измениться результат. Если дано выражение 5+2·4, видно, что вначале выполняется умножение, после чего сложение. Когда выражение будет иметь вид (5+2)·4, то вначале выполнится действие в скобках, после чего произведется умножение. Результаты выражений будут отличаться.
Выражения могут содержать несколько пар скобок, тогда выполнения действий начинаются с первой. В выражении вида (4+5·2)−0,5:(7−2):(2+1+12) видно, что первым делом выполняются действия в скобках, после чего деления, а в конце вычитание.
Существуют примеры, где имеются вложенные сложные скобки вида 4·6-3+8:2 и 5·(1+(8-2·3+5)-2))-4. Тогда начинается выполнение действий с внутренних скобок. Далее производится продвижение к внешним.
Пример 3
Если имеется выражение 4·6-3+8:2, тогда очевидно, что в первую очередь выполняются действия в скобках. Значит, следует отнять 3 от 6, умножить на 4 и прибавить 8. В конце следует разделить на 2. Только так можно получить верный ответ.
На письме могут быть использованы скобки разных размеров. Это делается для удобства и возможности отличия одной пары от другой. Внешние скобки всегда большего размера, чем внутренние. То есть получаем выражение вида 5-1:2+12+3-13·2·3-4. Редко встречается применение выделенных скобок (2+2·(2+(5·4−4)))·(6:2−3·7)·(5−3) или применяют квадратные, например, [3+5·(3−1)]·7 или фигурные <5+[7−12:(8−5):3]+7−2>:[3+5+6:(5−2−1)].
Перед тем, как приступить к решению, важно правильно определить порядок действий и разобрать все необходимые пары скобок. Для этого следует добавлять разные виды скобок или менять их цвет. Пометка скобки другим цветом удобна для решения, но занимает много времени, поэтому на практике чаще всего применяют круглые, фигурные и квадратные скобки.
Отрицательные числа в скобках
Если необходимо изобразить отрицательные числа, тогда применяют круглые скобки в выражении. Такая запись, как 5+(−3)+(−2)·(−1), 5+-23, 257-5+-673·(-2)·-3,5 предназначена для того, чтобы упорядочить отрицательные числа в выражении.
Скобки не ставятся для отрицательного числа того, когда оно располагается в начале любого выражения или дроби. Если имеем пример вида −5·4+(−4):2, то очевидно, что знак минуса перед 5 можно не заключать в скобки, а при 3-0,4-2,2·3+7+3-1:2 число 2,2 записано вначале, значит скобки также не нужны.
Общая характеристика
Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.
Значение и разновидности
Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.
В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.
Разновидности:
Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.
В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], < >(), [ ], < >. Также встречаются двойные, называемые обратными (]] и [ [) или > в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.
Основные цели квадратной скобки в математике:
Другие варианты расчета:
Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.
Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.
Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.
На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная < встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.
Одинарные или двойные выражения
Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.
В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.
Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.
По правилам интервал [−a;+a] записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.
В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.
В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).
Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0
Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.
Прочие знаки
Для математических, алгебраических и прочих расчетов важно знать различие обобщающих знаков. От правильности вычислений зависит итоговый результат.
Удобство записи системы уравнений
Применение фигурных знаков относится к представлению совмещения множеств. При решении системы с фигурной скобкой уравнения пересекаются, а [] объединяет их.
Как репетитор по математике оформляет объединение систем
Системы уравнений и неравенств входили в состав выпускных и вступительных экзаменов по математике во все времена. Даже если в экзаменационном варианте нет прямого задания на решение системы, то существует достаточно высокая вероятность ее появления процессе решения других задач. Репетитор по математике обязан это учитывать. Привести к системам могут задачи на модули, на логарифмы, на графики и даже на синусы с косинусы. Несмотря на то, что подготовка к ЕГЭ по математике нередко сводится к натаскиванию на решение однотипных номеров части «В», не стоит полностью отказываться от тренировки навыков поиска пересечения (объединения) ответов разных объектов. Хотя бы на элементарном уровне. Какими приемами репетитор по математике обеспечивает оптимальную работу ученика с системами? Какая техника оформления систем была бы самой удобной и продуктивной?
К сожалению, школьные учителя и даже некоторые профессиональные репетиторы требуют от детей (уже в 8 классе) оформление систем по принципу «все в одном», упаковывая содержащиеся в них неравенства в единый объект согласно строгим правилам проведения равносильных преобразований. Широко применяются квадратные и фигурные скобки, причем часто в весьма сложном сочетании. Мой опыт репетиторской работы свидетельствует о том, что дети с огромнейшим трудом воспринимают, казалось бы, несложные для математиков логические конструкции с конъюнкциями и дизъюнкциями. Примерно 60-70% всех школьников с трудом припоминают (или не знают вообще) чем отличается квадратная скобка от линейной. А среди тех, кто приходит к репетитору по математике, этот процент повышается в среднем до 90-95%.
Но, тем не менее, для обозначения объединения, некоторые школьные преподаватели все равно используют квадратные скобки. Видимо по привычке. При таком раскладе репетитор по математике оказывается в крайне сложном положении, ибо уровень ученика часто не позволяет осознать сложные логические сочетания. Я не сторонник любой ценой следовать школьным стандартам и часто полностью отказываюсь от постановки квадратных скобок. Без них проще. Особенно когда на носу подготовка к ЕГЭ. Если все же репетитор математики вынужден принимать школьные правила, он мог бы это сделать следующим образом:
Когда репетитор по математике вводит квадратную скобку?
Как видите, используется самое простое сочетание. Скобку лучше всего ввести после того, как ученик поймет суть задания. А она заключается в том, чтобы подобрать числа, обеспечивающие выполнение хотя бы одного неравенства (я употребляю общий термин: «условие»). Фразу «хотя бы одного» репетитор по математике сразу же меняет на фразу «или одно или другое». Процент учеников, правильно нашедших репетитору ответ, оказывается не таким и уж низким. Половина детей схватывают суть задания сразу же. Другим нужно показывать, как проверяется наугад взятое число (главное не объяснять только словами).
Данный номер рассматривается репетитором сразу после примера на совокупность, то есть на поиск числа, обеспечивающего выполнение каждого условия:
К сожалению, родители редко приглашают репетитора по математике в 8 классе и подготовкой к ЕГЭ занимаются только с 10 или с 11 класса. В этом случае репетитору приходится объяснять оформление объединения по формальному признаку фигурной скобки: если для проверки произвольно взятого числа достаточно проверить верность одного из нескольких условий (неравенств, уравнений или их систем), то проверяемые объекты можно заключить в квадратную скобку. Корректируя общую формулировку, репетитор по математике вставляет в нее союз «или». Например, для того, чтобы число x было корнем уравнения 
необходимо чтобы или первый множитель равнялся нулю, или второй. Преподаватель отдельно акцентирует внимание ученика на участии «или» и в случае его уместного употребления разрешает заключить объекты в квадратную скобку.
Если репетитор математики примет строгое оформление, он усложнит ученику одновременно и понимание и практическую работу. Школьные учителя берут за образец оформление систем в задачниках, в которых решения излагаются кратко. 
Из-за пропусков некоторых его частей удается компактно расписать все равносильные переходы, сохраняя целостность объекта. Репетитору по математике данная методика не подходит категорически. Почему? Ученики начинают вырывать по отдельности неравенства из огромной системы через весьма приличные промежутки времени. Переключение внимания на частные операции сбивает школьников с главного направления. Они забывают что именно им надо пересекать, а что объединять. Путаница возникает страшная. Хорошо, если репетитор по математике рядом и сможет подсказать. А что делать на ЕГЭ? Вряд ли стоит рисковать. Техника действий должна быть максимально прозрачной и удобной в практическом смысле.
Принимая квадратную скобку, репетитор по математике усложняет еще и сортировку решенного. Приходится оформлять отдельные неравенства в колонку (одно под другим) и запоминать какое именно решено, а какое еще нет. Если сами решения длинные, то ученику может не хватить страницы и придется ее переворачивать. Рассеивание внимания при этом гарантировано.
Может ли репетитор по математике обойтись без квадратной скобки
Да, вполне. Для этого применяются стрелочный эквивалент. Например: 
Чаще всего в объединение попадают две системы (если больше — лучше использовать иные методы изначально). В нашем случае одна из систем решается в левой части тетрадного листа, а другая в правой. Репетитор по математике разделяет квадратную скобку на две совокупности отдельных систем. На мой взгляд, это самая удобная форма для практической работы ученика. Почему? Те ответы, которые нужно пересечь, распределены по колонкам, при этом операции в левой и в правой колонке проводятся локально и не перемешиваются. Слева — свое пересечение, справа — свое. Очень удобно. Под каждой системой – решение. Системы не нужно вырывать из «квадратной скобки», не нужно переписывать. Финальные ответы, которые репетитор по математике и ученик получают слева и справа «сваливаются в общий ответ» без какой-либо коррекции и пересечения.
Исключение составляют случаи, когда промежутки имеют общую часть. Однако практика показывает, что даже если репетитор по математике забудет напомнить о «склеивании частей», то большинство учеников догадаются до него сами.
Преимущество стрелок для запоминания:
Когда ученик разделяет тетрадный лист на две части, то находясь на любом этапе решения по левой колонке, он помнит о том, что предстоит еще заполнить и правую часть. Это очень важно. Если вы репетитр, то наверняка знаете, что школьники часто забывают разобрать какой-нибуь случай или решить какое-нибдуь неравенство из системы.
Сложность работы с объединением и пересечением носит часто чисто технический характер и связана с проблемой механики решений, то есть запоминанием и сортировкой обрабатываемой информации. При подготовке к ЕГЭ по математике важно получить навык автоматического выполнения операций. Поэтому репетитору по математике крайне необходимо использовать в работе простые и удобные методы, каким является прием стрелочного разделения. Если потребуется объединить три или более системы, репетитор по математике может взять лист формата А4, развернуть его в длину и аккуратно решить задание распределяя системы по нескольким колонкам. Такой подход к оформлению позволит ученику четко разделить и запомнить логическую структуру объекта.
Репетитор по математике, Колпаков А.Н. Москва.
Скобки
Сюда перенаправляются запросы 🙂 и некоторые другие, начинающиеся с двоеточия. О них см. статью смайлик.
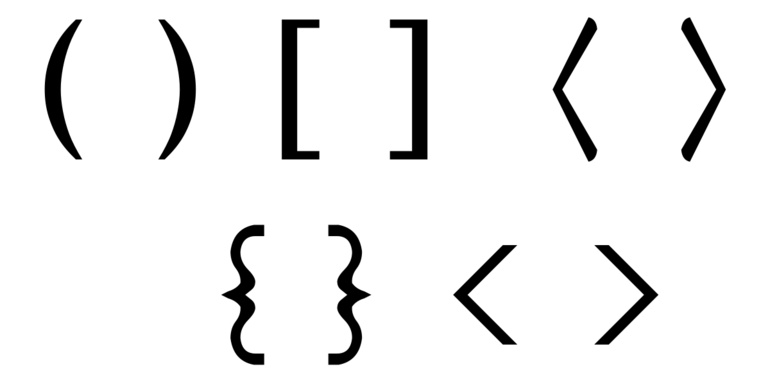
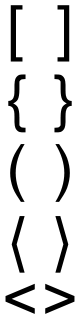
означает, что сначала выполняется логическое сложение 
а затем — логическое умножение 
Наряду с квадратными скобками используются также для записи компонент векторов:
для обозначения открытого сегмента и в некоторых других контекстах. Иногда круглыми скобками обозначается скалярное произведение векторов:
и «потолок» 
для обозначения ближайшего целого, не превосходящего 
, и ближайшего целого, не меньшего 
Как уже было сказано выше, иногда фигурными скобками обозначают антикоммутатор.
(кет-вектор) и 
(бра-вектор), их скалярное произведение как 
матричный элемент оператора А в определённом базисе как 
— среднее значение по времени от величины f.
.
являются самостоятельными символами. От « » их можно отличить по бо́льшему углу между сторонами — 
и 
" border="0" />.
.svg.png "Что значит фигурная скобка в функции. Смотреть фото Что значит фигурная скобка в функции. Смотреть картинку Что значит фигурная скобка в функции. Картинка про Что значит фигурная скобка в функции. Фото Что значит фигурная скобка в функции")
