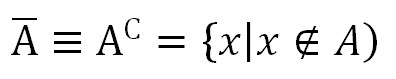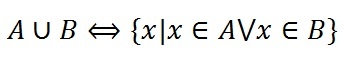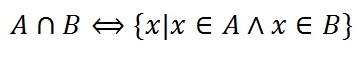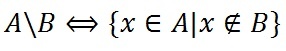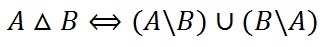Что значит эйлера венна
Диаграммы Эйлера—Венна
Круги́ Э́йлера [1] — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.
Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна, изображающие все 2 n комбинаций n свойств, то есть конечную булеву алгебру. При n = 3 диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако, этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц (1646—1716). Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы. [2]
Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер (1841—1902) в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют Диаграммы Эйлера — Венна.
Примечания
См. также
Ссылки
Полезное
Смотреть что такое «Диаграммы Эйлера—Венна» в других словарях:
Диаграммы Венна — Пример диаграммы Эйлера. B живое существо, A человек, C неживая вещь. Круги Эйлера[1] геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Эйлером. Используется в… … Википедия
ДИАГРАММЫ ВЕННА — ДИАГРАММЫ ВEHHА графический способ задания и анализа логико математических теорий и их формул. Строятся путем разбиения части плоскости на ячейки (подмножества) замкнутыми контурами (кривьми Жордана). В ячейках представляется информация,… … Философская энциклопедия
Круги Эйлера — Пример кругов Эйлера. Буквами обозначены, например, свойства: живое существо, человек, неживая вещь Круги Эйлера[1] геометрическая схема, с помощью которой можно изобразить отношения … Википедия
Диаграмма Эйлера — Пример диаграммы Эйлера. B живое существо, A человек, C неживая вещь. Круги Эйлера[1] геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Эйлером. Используется в… … Википедия
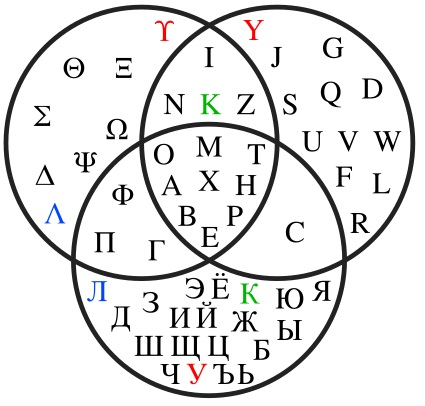
Диаграмма Венна — Диаграмма Венна, показывающая все пересечения греческого, русского и латинского алфавитов (буквы заглавные) Диаграмма Венна … Википедия
Логические диаграммы — графический (геометрический, точнее топологический) аппарат математической логики (См. Логика). Идея Л. д. была известна ещё в средние века, развивалась затем Г. В. Лейбницем, но впервые достаточно подробно и обоснованно была изложена Л.… … Большая советская энциклопедия
Формула включений-исключений — (или принцип включений исключений) комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом … Википедия
Операции над множествами — Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико множественными операциями или сет операциями. В результате операций из исходных множеств получаются новые … Википедия
Операция над множествами — Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико множественными операциями или сет операциями. В результате операций из исходных множеств получаются новые … Википедия
Кэрролл Льюис — (Carroll), настоящие имя и фамилия Чарлз Латуидж Доджсон (Dodgson) (1832 1898), английский писатель, математик и логик. В повестях сказках, продолжающих традицию гротескной «поэзии бессмыслиц», «Алиса в стране чудес» (1865) и «В Зазеркалье»… … Энциклопедический словарь
Как составить диаграмму Эйлера-Венна
Диаграмма Эйлера-Венна — что из себя представляет, где используется
Диаграмма Эйлера-Венна представляет собой геометрическую схему, предназначенную для представления моделей множеств и схем их взаимосвязей.
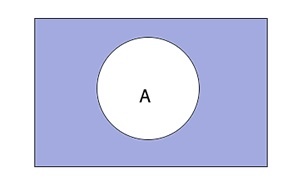
Благодаря данной диаграмме, приводят наглядное объяснение разных фактов о множествах. При таком методе универсальное множество представляют в виде прямоугольника, а для изображения подмножества используют круги. Широкое применение диаграммы Эйлера-Венна нашли в таких дисциплинах, как математика, логика, менеджмент, финансы и другие прикладные направления.
Способы отражения отношений между множествами ранее отличались. Джон Венн применял в качестве обозначения множеств замкнутые фигуры, а Эйлер – круги.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Диаграммы Эйлера-Венна представляют собой важный частный случай кругов, которые изображал Эйлер. На диаграммах представлены все 2 n комбинаций n свойств, что является конечной булевой алгеброй. Если n = 3, на диаграмме, как правило, изображают три круга с центрами, которые расположены в углах равностороннего треугольника, и совпадающими радиусами, ориентировочно равными длине сторон этого многоугольника.
Принципы построения, как изобразить множества
Построить диаграмму Эйлера-Венна – значит, составить большой прямоугольник, представляющий универсальное множество U, и разместить внутри него замкнутые фигуры в качестве обозначения множеств.
В том случае, когда требуется строить на диаграмме не более трех множеств, целесообразно использовать круги. Для изображения свыше четырех множеств применяют эллипсы. Пересечение фигур соответствует максимально общему случаю, согласно условиям задачи, и изображается должным образом на диаграмме.
Если предположить, что диаграмма содержит круг, обозначающий множество А, его центральная часть будет отражать истинность выражения А, а область вне круга – обозначать ложь. Те области, которые соответствуют истинным значениям, заштриховывают, что является отражением логической операции на диаграмме.
Согласно алгебре логики, конъюнкция множеств А и В соответствует истине в том случае, когда истинны оба эти множества. При этом на диаграмме отмечают участок пересечения множеств.
Применяя диаграммы Эйлера-Венна, доказывают любые алгебраические законы с помощью их графического изображения. Алгоритм построения:
Данные диаграммы являются эффективным методом визуализации операций с множествами. Отдельные множества изображают в виде кругов, а универсальное множество представляют прямоугольником.
Дополнение множества
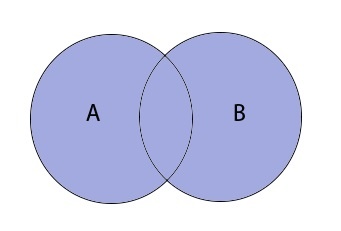
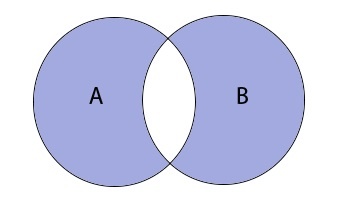
Объединение множеств
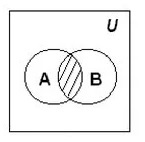
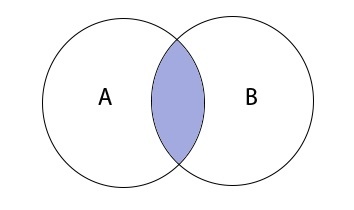
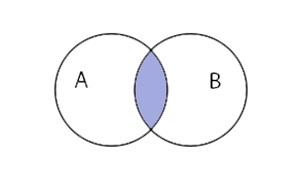
Пересечение множеств
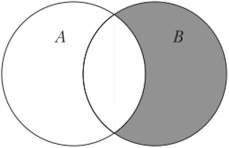
Разность множеств
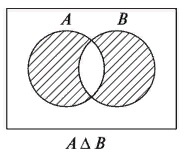
Симметричная разность множеств
Использование диаграмм Эйлера-Венна для доказательства логических равенств
В качестве доказательства логического равенства подходит способ построения диаграмм Эйлера-Венна. Для примера можно представить доказательства следующего выражения: ¬(АvВ) = ¬А&¬В. Равенство демонстрирует запись закона де Моргана. В первую очередь следует наглядно изобразить левую часть уравнения. Для этого необходимо последовательно заштриховать серым цветом все круги, то есть применить дизъюнкцию. Отобразить инверсию можно с помощью закрашивания черным цветом области вне этих кругов.
Далее следует визуально представить правую часть выражения. Последовательность действий в этом случае такова: необходимо заштриховать область, в которой отображается инверсия (¬А), с использованием серого цвета и аналогично закрасить область ¬В; отобразить конъюнкцию в виде пересечения этих серых областей. Результат такого наложения будет окрашен черным цветом.
На рисунке видно, что области, в которых отображены левая и правая части уравнения, равны друг другу. Таким образом, закономерность доказана.
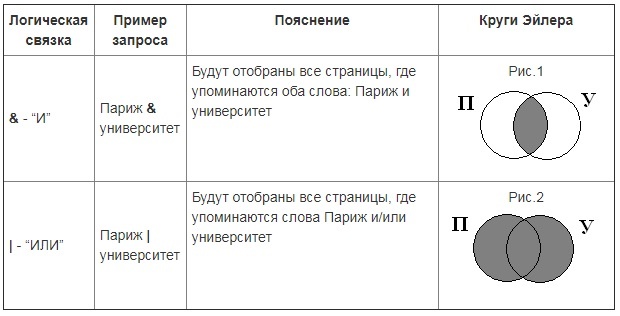
Решение задачи поиска информации в Интернет с помощью диаграмм Эйлера-Венна
Изучая тему поиска информации в глобальной сети Интернет, нельзя обойтись без примеров поисковых запросов, в которых использованы логические связки. Как правило, их смысл аналогичен союзам «и», «или» из русского языка. Принцип действия можно понять, если изобразить логические связи с помощью графической схемы или диаграммы Эйлера-Венна.
Как логические операции связаны с теорией множеств
Используя диаграммы Эйлера-Венна, принято наглядно демонстрировать связь логических действий и теории множеств. Операции логики можно задать с помощью таблиц истинности. В этом случае следует руководствоваться общим принципом.
На диаграмме в виде области круга под названием А отображают истинность определения А, то есть теоретически круг А обозначает все элементы, которые включены в данное множество. Таким образом, область за пределами круга А будет обозначать ложь соответствующего утверждения.
Понимание, какая область диаграммы отражает логическую операцию, возникает после того, как будут заштрихованы только те области, в которых значения логической операции на наборах А и В соответствуют истине. К примеру, импликация истинна при (00, 01 и 11).
Необходимо заштриховать сначала область за пределами пары пересекающихся кругов в соответствии со значениями А=0, В=0. Затем закрасить область в круге В, которая относится к значениям А=0, В=1, и область, соответствующую и кругу А, и кругу В, то есть участок пересечения, отображающий значения А=1, В=1. Эти три области в комплексе являются графическим представлением логической импликации.
Примеры задач с решением
Диаграммы Эйлера-Венна могут содержать три и более круга. Преимуществом данного графического способа представления выражений является его высокая эффективность и наглядность. К примеру, можно изобразить диаграмму пересечений букв из русского, латинского и греческого алфавита:
Понять суть методики удобно на практике. Можно решить несколько задач с применением диаграмм Эйлера-Венна.
Задача 1
По условию есть таблица поисковых запросов. В ней представлены страницы по некоторому сегменту. Требуется определить, сколько страниц в тысячах будет отображаться по запросу «Эсминец». Следует отметить, что запросы выполнялись практически в одно время, поэтому набор страниц с искомыми словами не менялся в процессе выполнения запросов.
Решение
Ф – является числом страниц (в тысячах) в соответствии с запросом «Фрегат»;
Э – является числом страниц (в тысячах) в соответствии с запросом «Эсминец»;
Х – представляет собой число страниц (в тысячах) по запросу, в котором присутствует «Фрегат» и отсутствует «Эсминец»;
У – определяет число страниц (в тысячах) по запросу, в котором указано слово «Эсминец» и отсутствует слово «Фрегат».
Диаграмма для каждого поискового запроса будет иметь следующий вид:
Исходя из информации по диаграммам, получим:
Х+900+У = Ф+У = 2100+У = 3400
Э = 900+У = 900+1300= 2200
Ответ: по запросу «Эсминец» будет найдено 2200 страниц
Задача 2
Класс состоит из 36 учеников. Дети ходят на занятия в рамках математического, физического, химического кружка. Факультатив по математике посещают 18 учащихся, по физике – 14, по химии – 10. Также известно, что 2 ученика ходят на все три кружка, 8 – на математику и физику, 5 – на математику и химию, 3 – на физику и химию. Необходимо определить количество учеников, которые не посещают ни одного кружка.
Решение
Решить данную задачу можно с помощью удобного и наглядного метода в виде кругов Эйлера. Наибольшим кругом следует обозначить множество всех учащихся класса. Внутри этой окружности необходимо изобразить пересекающиеся множества в виде учащихся на факультативе по математике (М), физике (Ф), химии (Х).
МФХ – является множеством учеников, каждый из которых ходит на занятия во все три кружка;
МФ¬Х – определяет множество учащихся, которые посещают факультативы по математике и физике, но не ходят на занятия по химии.
¬М¬ФХ – представляет собой множество людей, каждый из которых посещает химический факультатив, но отказался от дополнительных занятий по физике и математике.
По аналогичному принципу можно ввести множества: ¬МФХ, М¬ФХ, М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.
Согласно условиям задачи, пара учеников записаны во все три кружка. Поэтому в область МФХ требуется вписать число 2. Исходя из того, что 8 учащихся посещают факультативы по математике и физике, а из них двое школьников ходят во все кружки, то в области МФ¬Х следует отметить 6 человек (8-2). Аналогичным способом можно определить число учеников в остальных множествах:
Далее требуется определить сумму учеников по всем областям:
Таким образом, всего 28 учащихся посещают факультативные занятия.
Ответ: 8 учеников из класса не посещают ни одного кружка.
Задача 3
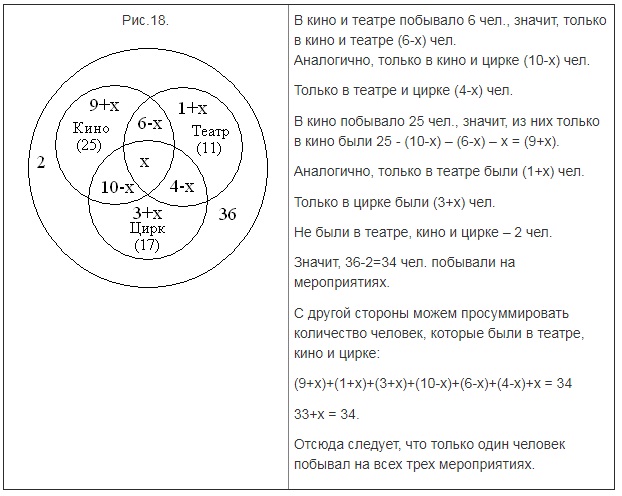
Когда закончились зимние каникулы, преподаватель поинтересовался у учеников, кто из них посещал театр, кино или цирк. Всего в классе 36 человек. По полученной информации, два ребенка не были ни в кино, ни в театре, ни в цирке. Кино посетили 25 школьников, театр – 11, цирк – 17. И в кино, и в театр сходили 6 человек, и в кино, и в цирк – 10, и в театр, и в цирк – 4. Необходимо посчитать, какое количество учащихся из класса посетили и кино, и театр, и цирк.
Решение
Предположим, что х представляет собой число учеников, которые посетили и кино, и театр, и цирк. В таком случае, можно изобразить диаграмму и определить число школьников для каждой области:
Ответ: 1 ученик побывал и в кино, и в театре, и в цирке.
Диаграммы Эйлера-Венна
Что такое диаграммы Эйлера-Венна
Диаграмма Эйлера-Венна — геометрическая схема, которая используется для моделирования множеств и для схематичного изображения и отношений между ними.Диаграмма позволяет наглядно отразить различные утверждения о множествах. При использовании этого метода универсальное множество изображается в виде прямоугольника, подмножества изображают кругами. Диаграммы нашли свое применение в математике, логике, менеджменте и других прикладных направлениях.
Для отражения отношений между множествами математики Джон Венн и Леонард Эйлер использовали для способа. Если Венн использовал для обозначения множеств замкнутые фигуры, то Эйлер использовал круги.
Диаграммы Эйлера-Венна являются важным частным случаем кругов Эйлера. Диаграммы изображают все 2^n комбинаций n свойств, что является конечной булевой алгеброй. В случае n = 3 диаграмма Эйлера-Венна обычно состоит из трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приближенно равным длине стороны треугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Принцип построения
Построение диаграммы Эйлера-Венна — это изображение большого прямоугольника, который представляет универсальное множество U. Внутри прямоугольника изображаются замкнутые фигуры, обозначающие множества. Если множеств не более 3, то изображаются круги, и эллипсы, если множеств 4. Фигуры пересекаются в наиболее общем случае, требуемом задачей, что обозначается соответствующим образом.
Предположим, что на диаграмме изображен круг, представляющий множество А. Область в середине круга множества А отражает истинность выражения А, в то время как область вне круга обозначает ложь. Логическая операция будет отображаться на диаграмме при помощи штриховки тех областей, в которых ее значения истинны. В соответствии с алгеброй логики, конъюнкция множеств А и B будет истинна только тогда, когда истинны оба множества. Тогда на диаграмме будет отмечена область пересечения множеств.
С помощью диаграмм Эйлера-Венна можно доказать все законы алгебры, представляя их графически. Это возможно через выполнение следующего алгоритма:
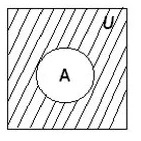
Дополнение множества
При этом не все элементы, не являющиеся элементами А, могут быть включены в \(\overline A.\) Принято считать, что все множества, которые участвуют в решении задачи, являются подмножествами некоторого общего универсального множества U. Учитывая это, дополнение \overline A определяется следующим образом:
Таким образом выглядит дополнение \(\overline A\) графически:
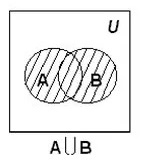
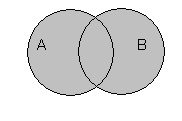
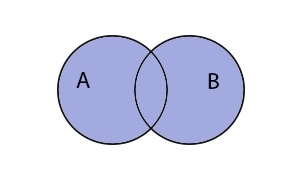
Объединение множеств
Объединение записывается следующим образом:
Таким образом объединение множеств выглядит графически:
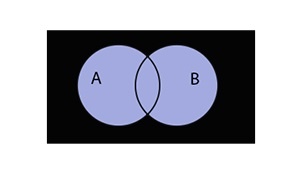
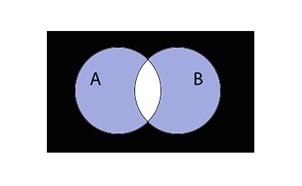
Пересечение множеств
Пересечение множеств записывается следующим образом:
Таким образом пересечение множеств выглядит графически:
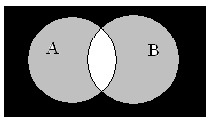
Симметричная разность множеств
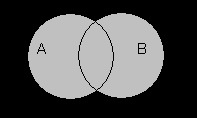
Симметричная разность A \ B — это такое множество, куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество
Разность множеств записывается следующим образом:
\(A\bigtriangleup B=(A\backslash B)\cup(B\backslash A)\)
Таким образом разность выглядит графически:
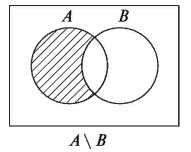
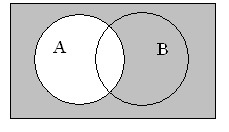
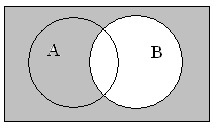
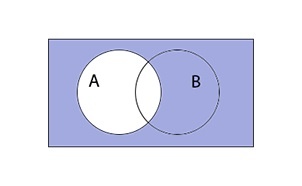
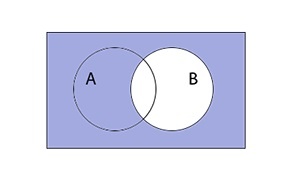
Разность множеств
Разностью A \ B является множество элементов A, не входящих в B.
Разность множеств записывается следующим образом:
Таким образом разность выглядит графически:
Использование диаграмм Эйлера-Венна для доказательства логических равенств
Рассмотрим, как диаграммы Эйлера-Венна применяются для доказательства логических равенств.
Предположим, что перед нами конъюнкция множеств \(A\;\wedge\;B\)
В первую очередь обратим внимание на левую часть равенства. Построим диаграмму для множеств А и B. Графически отметим дизъюнкцию, заштриховав оба круга цветом.
Теперь отобразим инверсию, заштриховав область за пределами множеств.
Обратим внимание на правую часть равенства. В первую очередь отобразим инверсию A штриховкой область за пределами круга множества A цветом.
Проведем аналогичную операцию с множеством B.
Теперь штриховкой черным цветом всех областей пересечения отобразим конъюнкцию инверсий множеств А и B.
При сравнении области для отображения правой и левой частей, становится очевидно, что они равны. Справедливость логического равенства доказана с помощью диаграммы Эйлера-Венна.
Примеры задач с решением
Задача
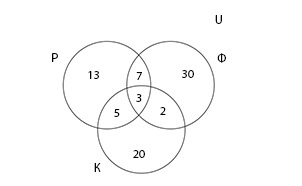
Группа туристов из 100 человек пробыла в городе N три дня. За это время в ресторане питались 28 туристов, фастфуде — 42, кофейне — 30. И в ресторане, и в фастфуде побывало 10 человек; в ресторане и кофейне — 8; в фастфуде и кофейне — 5. Все во всех трех местах побывали три человека. Сколько туристов питалось в других местах и не посетило ни одного из перечисленных?
Решение
В условии задачи три множества — Р, Ф и К. Туристы, которые пытались в ресторане, фастфуде и кофейне, соответственно. Универсальное множество U — это множество всех туристов группы. Запишем условие задачи, где n(X) — количество элементов множества X.
Необходимо найти \(n(Р\;\cup\;Ф\;\cup\;К)\;=\;n\;(U\;\backslash\;(Р\;\cap\;Ф\;\cap\:К))\)
В решении задачи поможет представление данных графически с помощью диаграммы Эйлера-Венна. Составляя ее, важно помнить, что если в \(Р\;\cap\;Ф\;\cap\:К\) три элемента, а в множестве \(Р\;\cap\;Ф\) — 10 элементов, то в диаграмме в месте пересечений множеств Р и Ф мы проставляем 7 элементов, так как 3 элемента уже учтено.
Теперь, когда на диаграмме все элементы учтены по одному разу, можно вычислить количество туристов, которые побывали хотя бы одном из заведений.
Тогда, количество туристов, которые не побывали ни в ресторане, ни в фастфуде, ни в кофейне можно вычислить следующим образом:
Ответ: 20 туристов не побывали ни в одном из указанных заведений.
Задача
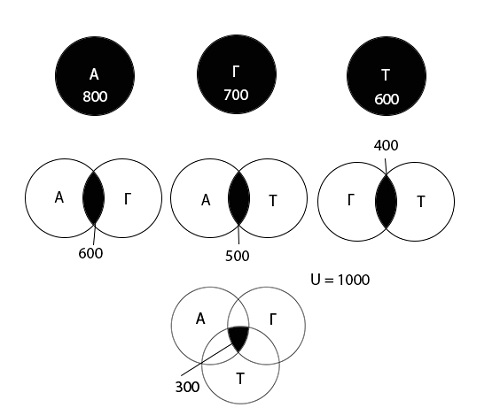
На олимпиаде по математике школьникам предложили решить три задачи: одну по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии — 700, по тригонометрии — 600. 600 школьников решили задачи по алгебре и геометрии, 500 — по алгебре и тригонометрии, 400 — по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько школьников не решило ни одной задачи?
Решение
Начнем с определения множеств и введения обозначений. В данном случае, их три:
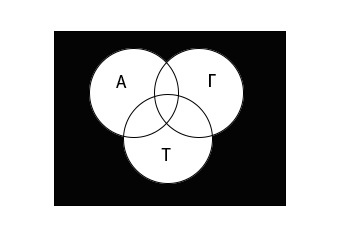
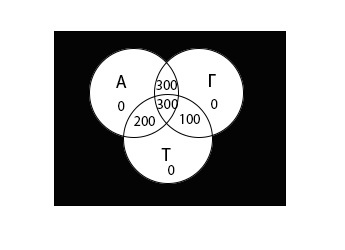
Используя диаграмму Эйлера-Венна графически изобразим информацию, данную в условии задачи.
Теперь используя диаграмму, обозначим область, которую необходимо найти:
Определим количество школьников для всех возможных областей.
Обозначим искомую область А = 0, Г = 0, Т = 0 как «х».
Найдем остальные области:
Теперь внесем значения всех областей в диаграмму:
\((A\;\cup\;Г\;\cup\;Т)\;=\; 0 + 0 + 0 + 300 + 300 + 200 + 100 = 900\)
Ответ: 100 школьников не решило ни одной задачи.