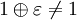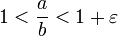Что значит эпсилон в эконометрике

Научный форум dxdy

Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

Определение предела и число эпсилон

1. Предел последовательности.
Цитирую:

2. Геометрический смысл того же предела последовательности:

Заранее благодарен за ответ.

Заслуженный участник

Заслуженный участник

Последний раз редактировалось ИСН 16.02.2013, 20:14, всего редактировалось 1 раз.

Заслуженный участник

Заслуженный участник

Заслуженный участник

Последний раз редактировалось henehen 16.02.2013, 22:34, всего редактировалось 3 раз(а).

PS. Причём, что самое интересное, такая привычка «объяснять» через левые переменные навроде эпсилонов и дельт сохраняется практически во всех учебниках и методичках, что весьма здорово способствует механическому использованию математики (не вникая ни во что) и убивает напрочь желание учиться.

И вообще, если кто-то мне объяснит человеческим языком на пальцах всю эту эпсилон-дельту технику, то я буду нечеловечески ему благодарен =)

Заслуженный участник

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Источник

Что такое точность epsilon?

Напишите программу, которая оценивает значение математической константы e по формуле e*=*1*+*1/1!*+*1/2!*+*1/3!*+*. с заданной введенной точностью epsilon.

ну вот написал я прогу, Е у меня высчитывается, а что за ЭПСИЛОН? какона работает как ее задать? зачем она ваще нужна и где могла бы пригодиться?

Что такое файловый буфер? Что такое режим (модификатор) доступа, при работе с файлами?
Что такое файловый буфер? Что такое режим (модификатор) доступа, при работе с файлами?

Что такое IIS и что такое PWS? Почему одно без другого не работает?
вот уже второй день пытаюсь немного разобраться в АСП. накидал небольшую тестовую страничку. но с.

Что такое рекурсивный тип данных? Что такое конструкция рекурсивного типа?
Что такое рекурсивный тип данных? Что такое конструкция рекурсивного типа?

Что такое напряжение и что такое сила тока с позиции заряженных частиц
Объясните пожалуйста, что такое напряжение и что такое сила тока с позиции заряженных частиц.

пошарил значит на википедии, и вот что там нашел:

Упоминания о чем-то схожем попадаются в книжке Подбельского В. В. » Введение в программирование на языке си » 2004 года, которую можно откопать, например тут, в ней, на странице 83 приведен алгоритм «оценки машинного нуля», и сдается мне, что этот мышиный ноль именно то, что вам нужно. Если описать эту зверушку в коде, получится примерно так:

результат вывода странный, что я делаю не так?

Добавлено через 17 минут
например при EPSILON = 0.5 а X = 2 выдает INF в выводе

Добавлено через 36 минут
Только что заменил глупую ошибку в функции подсчета, вроде заработало, но прошу экспертной оценки

— очень плохой код. Прежде, чем программировать, нужно вывести рекуррентную формулу, которая связывает следующий член ряда с предыдущим:

Если что, мой пост был не с целью критики а анализ библиотечной реализации, вашей и SadiQ228‘а. Как ни странно, по эффективности методы не так уж сильно отличались. ну за исключением того, что вычисление факториала и степени с нуля давало громадную ошибку. Но это я еще перепроверю

Добавлено через 1 час 16 минут
Итак, результаты
библиотечный exp(): 0.040448 мкс
функция SadiQ228’а: 1.07945 мкс
функция Catstail’а: 0.142243 мкс
То есть способ с использованием предыдущего значения в 7,5 раз быстрее «лобового», но в 3,5 раза медленнее библиотечного (наверняка там пошаманили с оптимизациями). Если поставить epsilon = 1e-5 то результаты ближе:
exp(): 0.040998
SadiQ228’а: 0.814409
Catstail’а: 0.0630968

ребят, продолжая тему точности, пытаюсь высчитать E по другому ряду.
1/e = (-1)^n/n!; n=2

пытаюсь сделать но ответы удивляют, подскажите где ошибаюсь?

Решение

Легко. Просто надо вспомнить, что n! = n*(n-1)!

Добавлено через 8 минут

Типа того. А где ты здесь видишь факториалы? Хотя они, конечно, есть

Источник

Сущность регрессионного анализа

Регрессионный анализ заключается в определении аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков, а множество всех прочих факторов также оказывающих влияние на результативный признак, принимается за постоянные и средние значения.

Цель регрессионного анализа – это оценка функциональной зависимости условного среднего значения результативного признака от факторных признаков.

Теоретическая обоснованность моделей

Условия теоретической обоснованности моделей:

1. Все приззнаки и их совместные распределения должны подчиняться нормальному закону распределения;

2. Дисперсия моделируемого признака должна все время оставаться постоянной при изменении величины и значений факторных признаков.

3. Отдельные наблюдения должны быть независимыми, т.е. результаты, полученные в i-м наблюдении не должны быть связаны с предыдущими и содержать информацию о последующих наблюдениях, а так же влиять на них.

Примеры взаимосвязи между переменными

1 – График, от левого нижнего в правый верхний линия, точки на ней и вокруг неё.

а) взаимосвязь между Х и У близка к линейной: У = a+bX;

б) взаимосвязь близка к квадратической: Y = a+bX+cX 2

в) Взаимосвязь между X и Y отсутствует. Какую бы мы ни выбрали форму связи, результаты проверки её качества будут неудачными.

Уравнение линейной парной регрессии

Y(x) = ^y(x)+эпсилон = a+bx+эпсилон

Где a, b – параметры модели, Эпсилон – случайная величина (величина остатка)

A – свободный коэффициент регрессионного уравнения. Не имеет экономического смысла и показывает значение результативного признака y. Если факторный признак x=0.

B – коэффициент регрессии показывает, на какую величину в среднем изменится результативный признак у, если переменную х увеличить на единицу измерения. Знак при коэффициенте регрессии показывает направление связи.

Эпсилон – независимая, нормально распределенная случайная величина, остаток с нулевым математическим ожиданием и постоянной дисперсией. Отражает тот факт, что изменение у будет неточно описываться изменением х, т.к. присутствуют и другие факторы, не учтенные в данной модели.

Коэффициент эластичности показывает на сколько процентов изменяется результативный признак y при изменении факторного признака x на 1 процент.

Э_yx= b (x с чертой / y с чертой)- только для линейной регрессии.

Источник

что какой эпсилон

Ε, ε (название: э́псилон, греч. έψιλον) — 5-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 5. Происходит от финикийской буквы hé — hé. От буквы «эпсилон» произошли латинская E и кириллическая Е. Название «эпсилон» (греч. Ε ψιλόν — «е простое» ) было введено для того, чтобы отличать эту букву от созвучного сочетания αι.
Использование

Заглавная буква эпсилон в основном не используется как символ, поскольку пишется так же, как и заглавная латинская буква E.

В различных дисциплинах при помощи строчной буквы ε обозначаются:

в математическом анализе — положительное сколь угодно малое вещественное число; см. примеры в статье Предел последовательности;
в алгебре — предельное порядковое число последовательности \omega,\omega^<\omega>,\omega^<\omega^<\omega>>,\dots.
в теории множеств — отношение принадлежности элемента множеству (такое обозначение является устаревшим, сейчас для той же цели используется символ ∈);
в тензорном исчислении — символ Леви-Чивиты;
в теории автоматов — эпсилон-переход;
в физике — угловое ускорение; коэффициент экстинкции оптического поглощения; проводимость среды; электронный захват; относительное удлинение; диэлектрическая проницаемость среды; энергия активации; ЭДС; ε0 — универсальная электрическая постоянная.
в астрономии — пятая (как правило) по яркости звезда в созвездии;
в программировании — точность численного типа данных;
в информатике — пустая строка;
в фонетике — неогубленный гласный переднего ряда средне-нижнего подъёма.
в теории метаболического контроля — эластичность фермента

Источник

Машинный эпсилон

Плавающая запятая — форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто используемое представление утверждено в стандарте IEEE 754. Реализация математических операций с числами с плавающей запятой в вычислительных системах может быть как аппаратная, так и программная.

Содержание

«Плавающая запятая» и «плавающая точка»

Так как в некоторых, преимущественно англоязычных и англофицированных, странах (см. подробный список Decimal separator (англ.) ) при записи чисел целая часть отделяется от дробной точкой, то в терминологии этих стран фигурирует название «плавающая точка» (floating point (англ.) ). Так как в России целая часть числа от дробной традиционно отделяется запятой, то для обозначения того же понятия используется термин «плавающая запятая».

Происхождение названия

Название «плавающая запятая» происходит от того, что запятая в позиционном представлении числа (десятичная запятая, или, для компьютеров, двоичная запятая — далее по тексту просто запятая) может быть помещена где угодно относительно цифр в строке. Это положение запятой указывается отдельно во внутреннем представлении. Таким образом, представление числа в форме с плавающей запятой может рассматриваться как компьютерная реализация экспоненциальной записи чисел.

Преимущество использования представления чисел в формате с плавающей запятой над представлением в формате с фиксированной запятой (и целыми числами) состоит в том, что можно использовать существенно больший диапазон значений при неизменной относительной точности. Например, в форме с фиксированной запятой число, занимающее 8 разрядов в целой части и 2 разряда после запятой, может быть представлено в виде 123456,78; 8765,43; 123,00 и так далее. В свою очередь, в формате с плавающей запятой (в тех же 8 разрядах) можно записать числа 1,2345678; 1234567,8; 0,000012345678; 12345678000000000 и так далее.

Скорость выполнения компьютером операций с числами, представленными в форме с плавающей запятой, измеряется в англ. FLOPS — число операций с плавающей запятой в секунду ),

Структура числа

Число с плавающей запятой состоит из:

Нормальная форма

Использование в вычислительных машинах

Краткий обзор

Существует несколько способов того, как строки из цифр могут представлять числа:

Запись числа в форме с плавающей запятой позволяет производить вычисления над широким диапазоном величин, сочетая фиксированное количество разрядов и точность. Например, в десятичной системе предоставления чисел с плавающей запятой (3 разряда) операцию умножения, которую мы бы записали как

в нормальной форме представляется в виде

(1,20 × 10 −1 ) × (1,20 × 10 −1 ) = (1,44 × 10 −2 ).

В формате с фиксированной запятой мы бы получили вынужденное округление

Мы потеряли крайний правый разряд числа, так как данный формат не позволяет запятой «плавать» по записи числа.

Диапазон чисел, представимых в формате с плавающей запятой

Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. На обычной 32-битной вычислительной машине, использующей двойную точность (64 бита), мантисса составляет 52 бита + 1 знаковый, показатель — 11 бит. Таким образом получаем диапазон точности примерно от 4,94 × 10 −324 до 1.79 × 10 308 (от 2 −52 × 2 −1022 до

1 × 2 1024 ). Пара значений показателя зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся значения бесконечность), получающихся в результате операций типа деления на ноль нуля, положительных и отрицательных чисел. Также сюда попадают денормализованные числа, у которых мантисса меньше единицы. В специализированных устройствах (например GPU) поддержка специальных чисел часто отсутствует. Существуют программные пакеты, в которых объём памяти выделенный под мантиссу и показатель задаётся программно, и ограничивается лишь объёмом доступной памяти ЭВМ.

Машинный эпсилон

В отличие от фиксированной запятой, сетка чисел, которые способна отобразить арифметика с плавающей запятой, неравномерна: она более густая для чисел малого порядка и более редкая — для больших чисел. Но относительная погрешность записи чисел одинакова и для малых чисел, и для больших. Поэтому можно ввести понятие машинного эпсилона.

Машинным эпсилоном называется наименьшее положительное число ε такое, что (знаком обозначено машинное сложение). Грубо говоря, числа a и b, соотносящиеся так, что , машина не различает.

Источник