Что значит экстремумы функции
Максимумы, минимумы и экстремумы функций
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.
Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. \(y\). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, \(-5\) точка минимума (или точка экстремума), а \(1\) – минимум (или экстремум).
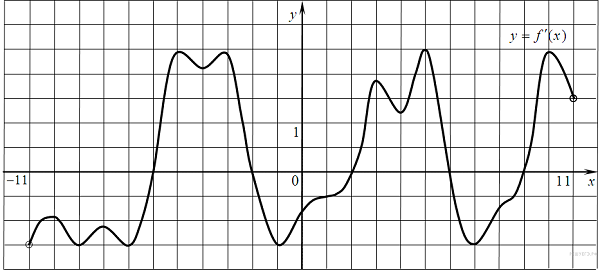
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось \(x\)).
Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.
Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди \(-13\), \(-11\), \(-9\),\(-7\) и \(3\).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.
\(-11\): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что \(-11\) – это минимум.
\(- 9\): функция возрастает, а потом убывает – максимум.
Все вышесказанное можно обобщить следующими выводами:
— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.
Пример(ЕГЭ). Найдите точку максимума функции \(y=3x^5-20x^3-54\).
Решение:
1. Найдем производную функции: \(y’=15x^4-60x^2\).
2. Приравняем её к нулю и решим уравнение:
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является \(-2\).
Возрастание и убывание функции на интервале, экстремумы
Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.
Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.
Возрастание и убывание функции на интервале
Точки экстремума, экстремумы функции
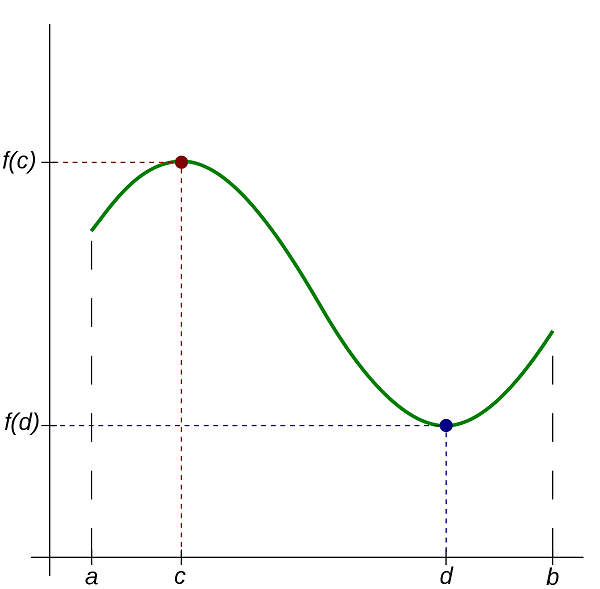
Окрестностями точки х 0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.
Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.
Достаточные условия возрастания и убывания функции
Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.
Первое достаточное условие экстремума
Иначе говоря, получим их условия постановки знака:
Алгоритм для нахождения точек экстремума
Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:
Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.
Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.
Точка х = 5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид
Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:
После чего необходимо найти производную:
Точка х = 0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:
Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:
Изображение на прямой имеет вид
Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что
Перейдем к вычислению минимумов:
Произведем вычисления максимумов функции. Получим, что
Второй признак экстремума функции
Для начала находим область определения. Получаем, что
Необходимо продифференцировать функцию, после чего получим
Третье достаточное условие экстремума
Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что
Из выше решенного делаем вывод, что x 3 = 3 является точкой минимума функции.
Что такое экстремумы функции: критические точки максимума и минимума
Из данной статьи читатель узнает о том, что такое экстремум функционального значения, а также об особенностях его использования в практической деятельности. Изучение такого концепта крайне важно для понимания основ высшей математики. Эта тема является основополагающей для более глубокого изучения курса.
Что такое экстремум?
В школьном курсе дается множество определений понятия «экстремум». Данная статья призвана дать самое глубокое и четкое представление о термине для несведущих в вопросе лиц. Итак, под термином понимают, насколько функциональный промежуток приобретает минимальное либо максимальное значение на том или ином множестве.
Экстремум – это и минимальное значение функции, и максимальное одновременно. Различают точку минимума и точку максимума, то есть крайние значения аргумента на графике. Основные науки, в которых используют данный концепт:
Точки экстремума играют важную роль в определении последовательности заданной функции. Система координат на графике в лучшем виде показывает изменение экстремального положения в зависимости от изменения функциональности.
Это интересно! Свойства натуральных логарифмов: график, основание, функции, предел, формулы и область определения
Экстремумы производной функции
Имеет также место такое явление, как «производная». Она необходима для определения точки экстремума. Важно не путать точки минимума либо максимума с наибольшим и наименьшим значением. Это разные понятия, хотя могут показаться похожими.
Значение функции является основным фактором для определения того, как найти точку максимума. Производная не образуется от значений, а исключительно от крайнего ее положения в том или ином его порядке.
Сама же по себе производная определяется на основе данных точек экстремума, а не наибольшего или наименьшего значения. В российских школах недостаточно четко проводят грань между этими двумя концептами, что влияет на понимание данной темы вообще.
Это интересно! Как определить определенные интегралы от нуля, константы и с доказательством
Острый экстремум
Давайте теперь рассмотрим такое понятие как «острый экстремум». На сегодняшний день выделяют острый минимум значения и острый максимум значения. Определение дано в соответствии с российской классификацией критических точек функции. Концепт точки экстремума лежит в основе нахождения критических точек на графике.
Экстремальное значение функции
Для определения такого понятия прибегают к использованию теоремы Ферма. Она является важнейшей в ходе изучения крайних точек и дает четкое представление об их существовании в том или ином их виде. Для обеспечения экстремальности важно создать определенные условия для убывания либо возрастания на графике.
Для точного ответить на вопрос «как найти точку максимума», необходимо следовать таким положениям:
Необходимое условие экстремума функции
Для того чтобы существовал экстремум, важно, чтобы были как точки минимума, так и точки максимума. В случае если это правило соблюдено лишь частично, то условие существование экстремума нарушается.
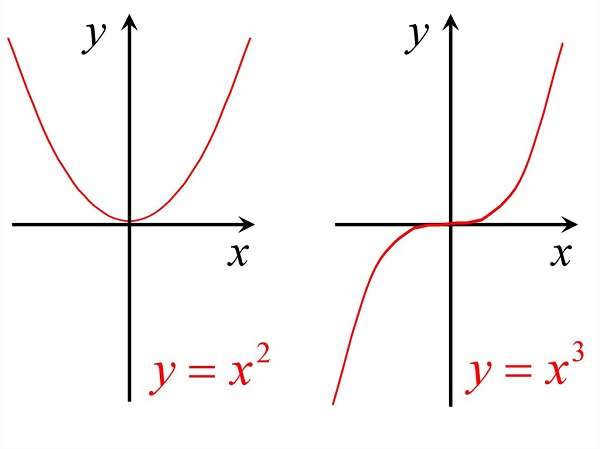
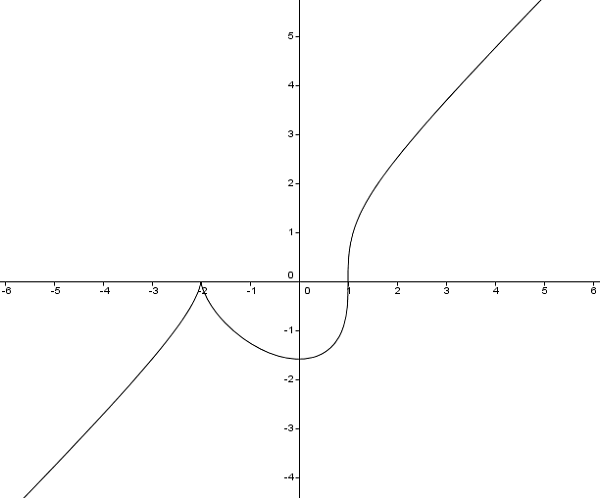
Каждая функция в любом положении должна быть продифференцирована с целью выявления ее новых значений. Важно понимать, что случай обращения точки в ноль не является основным принципом нахождения дифференцируемой точки.
Острый экстремум, также как и минимум функции – это крайне важный аспект решения математической задачи с использованием экстремальных значений. Для того чтобы лучше понимать данную составляющую, важно обратиться к табличным значениям по заданию функционала.


















 не имеет производной при x=0, так как
не имеет производной при x=0, так как  обращается в бесконечность приx=0. Но в этой точке функция имеет максимум.
обращается в бесконечность приx=0. Но в этой точке функция имеет максимум.
 не имеет производной при x=0, так как
не имеет производной при x=0, так как  при x→0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x)=0 и при x 0f(x)>0.
при x→0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x)=0 и при x 0f(x)>0.
 .
.


 . Производная не существует при х2= 0. Следовательно, критические точки: 0 и 2/5. Нанесем их на числовую ось и определим знак производной на каждом из полученных промежутков.
. Производная не существует при х2= 0. Следовательно, критические точки: 0 и 2/5. Нанесем их на числовую ось и определим знак производной на каждом из полученных промежутков.











 .
. .
. .
.

 .
.
 .
. . Отсюда
. Отсюда  .
. , по смыслу задачи 0≤h≤2R.
, по смыслу задачи 0≤h≤2R. .
.