Что значит что векторы компланарны
Компланарность векторов. Условия компланарности векторов.
 |
| рис. 1 |
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Условия компланарности векторов
Примеры задач на компланарность векторов
Решение: найдем смешанное произведение векторов
Ответ: вектора не компланарны так, как их смешанное произведение не равно нулю.
Решение: найдем смешанное произведение векторов
Ответ: вектора компланарны так, как их смешанное произведение равно нулю.
Решение: найдем количество линейно независимых векторов, для этого запишем значения векторов в матрицу, и выполним над ней элементарные преобразования
 | 1 | 1 | 1 |  |
| 1 | 2 | 0 | ||
| 0 | -1 | 1 | ||
| 3 | 3 | 3 |
из 2-рой строки вычтем 1-вую; из 4-той строки вычтем 1-вую умноженную на 3




к 3-тей строке добавим 2-рую


Так как осталось две ненулевые строки, то среди приведенных векторов лишь два линейно независимых вектора.
Ответ: вектора компланарны так, как среди приведенных векторов лишь два линейно независимых вектора.
Компланарные векторы и условие компланарности
В данной статье мы рассмотрим такие темы, как:
Определение компланарных векторов
Компланарные векторы — это векторы, которые параллельны одной плоскости или лежат на одной плоскости.
Два любых вектора всегда компланарны, поскольку всегда можно найти плоскости параллельные 2-м произвольным векторам.
Условия компланарности векторов
Примеры решения задач на компланарность векторов
Исследуем на компланарность векторы
Как решить?
Векторы будут являться компланарными, если их смешанное произведение равно нулю, поэтому вычисляем смешанное произведение заданных векторов. Для этого составляем определитель, по строкам которого записываются координаты векторов-сомножителей:
Отсюда следует, что смешанное произведение не равняется нулю, поэтому векторы не являются компланарными.
Ответ: векторы не являются компланарными.
Докажем, что три вектора
Как решить?
Находим смешанное произведение данных векторов:
Из данного примера видно, что смешанное произведение равняется нулю.
Ответ: векторы являются компланарными.
Проверим, компланарны ли векторы
Как решить?
Необходимо найти количество линейно независимых векторов: записываем значения векторов в матрицу и выполняем элементарные преобразования:
Из 2-ой строки вычитаем 1-ю, из 4-ой вычитаем 1-ю, умноженную на 3:
К 3-ей строке прибавляем 2-ю:
Поскольку в матрице только две ненулевые строки, делаем вывод, что среди них всего два линейно независимых вектора.
Ответ: векторы являются компланарными, поскольку среди них всего два линейно независимых вектора.
Общие сведения
Под вектором в математике принято понимать линию, которая имеет начало и конец. Иными словами, это отрезок. При этом имеет значение его направление, то есть знание начальной точки и конечной. Расположение векторов в пространстве или на плоскости определяется их координатами. Они соответствуют проекциям отрезка на координатные оси.
Над отрезками можно выполнять различные действия. Их можно между собой складывать или вычитать, умножать на произвольное число, находить произведение. Последнее может быть скалярным или смешанным. Немаловажным параметром является и длина вектора. Находят её путём вычитания из конечных координат начальных. Если векторов несколько, то на их базе строят геометрические фигуры, с помощью которых находят нужные параметры.
Все векторы разделяют по расположению в пространстве на следующие виды:
Изображение геометрической проекции отрезков на координатных осях называют расположением по базису. За него чаще всего выбирают координатные орды. При исследовании свойств вначале выполняют графическое изображение, а после переходят к алгебраическому расчёту. Это очень удобно и применяется повсюду.
Обозначают вектор двумя заглавными буквами, символизирующими начальную точку и конечную, а сверху ставится стрелочка или риска. Кроме этого отрезок часто обозначают и просто маленькой латинской буквой с чёрточкой. Например, AB или a.
Отрезки на плоскости
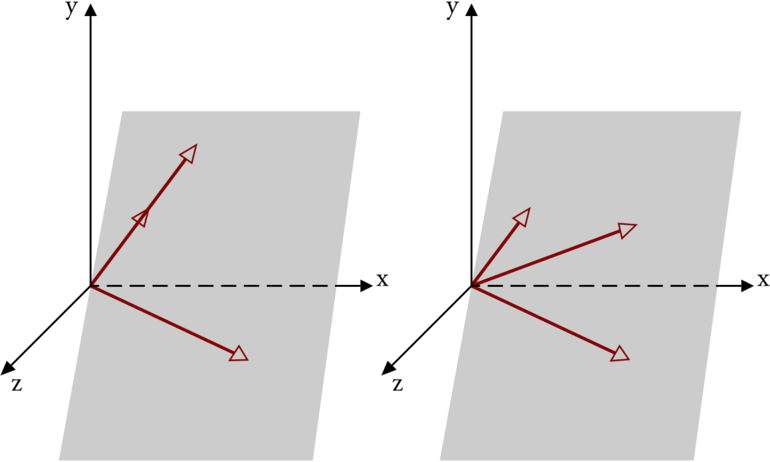
Условия, при которых отрезки являются компланарными, изучают в одиннадцатом классе средней школы на уроках геометрии. Так как на одной плоскости условие критерия всегда выполняется, то рассматривается их положение в пространстве. Согласно определению, векторы называются компланарными, если при откладывании их от произвольной точки они будут находиться в одной плоскости. То есть на признак не влияет длина и направление.
Для наглядности определения можно провести эксперимент. Взять три карандаша и расположить их на столе. В этом случае признак компланарности векторов выполняется, они лежат на одной плоскости. Затем параллельно ей приподнять два карандаша перпендикулярно вверх. Они так же будут являться компланарными, так как, если их отложить от одной точки, они будут всё равно лежать в одной плоскости.
Пусть имеются два вектора, a и b, направленные из одной точки. Любая третья ограниченная линия C в плоскости однозначно разлагается по этим неколлинеарным отрезкам: c = xa + yb. Это соотношение берётся из геометрического построения. Если из конца отрезка C опустить линию, параллельную b, а вектор a продлить до пересечения с ней в точке D, то образуется треугольник и отрезок AD коллинеарный a (AD||a). Это обозначает, что существует число икс, при котором получается новый отрезок: AD = xa.
Теперь из точки C нужно провести прямую параллельную AD и рассмотреть вектор AB в нарисованном параллелограмме. Получается, что он параллелен b (AB||b). А это может быть только тогда, когда существует такое число игрек, что оно, умноженное на число b, даст в точности отрезок AB. Отсюда следует, что в плоскости к любому третьему вектору можно применить разложение единственным образом.
Если вектор C можно разложить по линиям a и b, то есть записать как c = xa + yb, где x и y конкретные числа, то эти три отрезка компланарные. Это и есть условие компланарности векторов с простым его доказательством.
Действительно, если рассмотреть чертёж, то можно явно увидеть, что все три линии a, b, c лежат в одной плоскости, образованной их направлениями. Иными словами, три линии, имеющие начало и конец, будут компланарными при условии, что среди них есть пара коллинеарных отрезков. Тогда через коллинеарный и неколлинеарный вектор можно пропустить плоскость, и оставшийся отрезок перенести на неё.
Компланарность в пространстве
Пусть имеются три ограниченных линии в пространстве. Из них можно построить параллелепипед, имеющий общую точку O. Если на плоскости сумма отрезков ищется по правилу треугольника или параллелограмма, то в пространстве используется теорема о многоугольнике. На чертеже следует изобразить диагональ, обозначив её конечную точку буквой F.
Диагональная линия OF по правилу параллелепипеда будет находиться как сумма образующих отрезков: OF = a + b + c. Если в плоскости имеются два неколлинеарных вектора, то можно владеть линиями, принадлежащими ей, то есть третий вектор однозначно разлагается по этим коллинеарным отрезкам. В пространстве же нужны для этого три некомпланарные ограниченные линии.
Это значит, что, если их отложить, они не будут лежать в одной плоскости. Отсюда следует прямая зависимость с четвёртым отрезком, находящимся в пространстве. Она заключается в том, что он однозначно разлагается по трём некомпланарным линиям.
Этот принцип описывается теоремой: любой четвёртый вектор в пространстве будет равняться сумме трёх отрезков, каждый из которых умножен на конкретное число. Равенство записывают в виде формулы: p = xa + yb + xc. При этом если отрезок можно представить как сложение трёх линий в пространстве, то говорят о его разложении, а числа, используемые в записи, называют коэффициентами разложения. Это необходимое условие для выполнения теоремы.
Для доказательства необходимо построить четыре отрезка. Причём a, b, c будут не компланарными, а четвёртая линия будет произвольной в пространстве. Все векторы отложены от одной точки. Выходящие из одной точки a и b образуют плоскость. Из конечной точки P можно опустить перпендикуляр на ось b, тем самым построив прямоугольник. Точка соприкосновения с осью пусть будет P1. Тогда PP1 = zC. Это следует из коллинеарности. Так как P = OP1 + PP1, а OP1 = xa + yb, то, подставив эти выражения линейных комбинаций, можно записать, что P = xa + yb + zc.
Можно утверждать, если существуют такие числа x, y, z, то любую линию, имеющую начало и конец, можно разложить в линейную комбинацию по трём векторам. При этом такое разложение единственное. Проверить это утверждение достаточно просто, если идти от обратного.
Необходимое условие
При решении заданий обязательно нужно понимать, как можно проверить компланарность векторов. Для этого используется понятие смешанного произведения.
Следует рассмотреть векторное произведение отрезков a и b. По сути, это есть некий отрезок, который можно скалярно умножить на вектор c. При таком умножении в ответе должно получиться число (скаляр). Поэтому произведение вида (a x b) * c имеет конкретное численное значение. Такое произведение и называется смешанным.
Пусть имеются векторы с однозначными координатами:
Тогда смешанное произведение можно найти как определитель третьего порядка. Полученное вычисление очень важно, так как по полученному ответу можно судить о компланарности. Если смешанное произведение равняется нулю — векторы компланарны. В ином случае они некомпланарные и говорят, что они образуют базис пространства. Отсюда следует, что необходимым и достаточным условием компланарности трёх векторов является то, что смешанное их произведение равняется нулю a x b * c = 0.
Решение задачи
Теоретические аспекты любой темы лучше всего понимаются при наглядном их использовании. Поэтому важное место в геометрии и аналитической математике занимают практические задания. Вот пример одной из задач, для решения которой достаточно знать свойства компланарности отрезков и разложение по базису.
Для этого на первом шаге нужно найти смешанное произведение и установить соответствие компланарности. Делается это через составление определителя:
Искомое разложение имеет вид линейной комбинации отрезков: x = a * p + b * q + t * r, где a, b, t — коэффициенты разложения. Поэтому на втором шаге и нужно найти эти числа. Для того чтобы отрезок умножить на число, необходимо каждую его координату перемножить с ним:
Использование онлайн-калькулятора
Проверка на условие компланарности обычно не вызывает трудностей в решении примеров из школьного курса. Но на практике, особенно физикам, приходится сталкиваться с большими числами, при этом часто в системе уравнений стоят дробные члены. Поэтому при сложных расчётах благоразумно будет использовать автоматические решатели.
Это такие онлайн-сервисы, которые предоставляют услуги по вычислению различных математических параметров. От пользователя требуется лишь точно ввести в предложенную форму исходные данные и нажать кнопку «Вычислить». Система автоматически рассчитает ответ и выдаст его на дисплей.
Из существующих онлайн-калькуляторов, предоставляющих бесплатно возможность проверки вектора на компланарность, можно выделить:
Эти сервисы доступны на русском языке. Их страницы не содержат рекламного кода. При этом интерфейс интуитивно понятен.
На всех сайтах имеется информация по проверке векторов на параллельность, компланарность и другие свойства. Поэтому даже неподготовленный пользователь сможет разобраться, откуда взялась в ответе та или иная цифра.
Для удобства пользователь может включить подробное решение. В таком случае ему будет доступно посмотреть каждое действие, связанное с решением задачи, причём с короткими комментариями. Поэтому онлайн-калькуляторы довольно востребованы как среди школьников, студентов, так и среди инженеров, выполняющих ряд сложных векторных вычислений.
Какие векторы называют компланарными
Компланарные векторы – это векторы, которые лежат в одной плоскости, или параллельны какой-либо плоскости.
Рассмотрим три вектора в трехмерном пространстве. Любые два из них будут компланарными всегда. Поэтому, компланарность проверяют минимум для трех векторов.
Почему любые два вектора всегда компланарны
Поясним факт, что любые два вектора будут компланарными.
Для начала вспомним, какие векторы называют равными. Равны векторы, у которых совпадают три характеристики: длина, направление, соответственные координаты.
При параллельном переносе вектор не поворачивается. Этот новый вектор \( \vec
\[ \vec = \vec
Если два вектора равны, то вместо одного из них мы сможем использовать второй, когда это будет удобным для нас.
Проделаем теперь те же операции с каким-либо другим вектором \( \vec \). В результате получим вектор \( \vec
Любые два вектора можно параллельным переносом сдвинуть так, чтобы совместить их начальные, или конечные точки. Значит, через эти векторы можно провести пересекающиеся прямые. А такие прямые будут лежать в одной плоскости.
Таким образом, любые два вектора всегда компланарны.
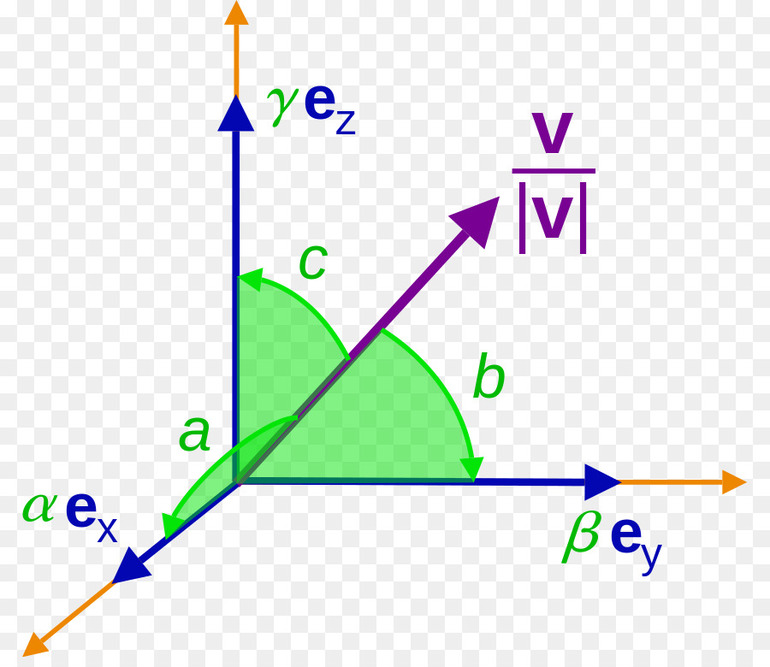
Например, любые два орта Декартовой прямоугольной системы координат компланарны, а тройка ортов – некомпланарные векторы. Подробнее об ортах тут (откроется в новой вкладке).
Условие компланарности
Найдем смешанное произведение трех векторов.
Если такое произведение будет равно нулю, то три вектора компланарные.
Условие компланарности векторов:
\[\large \boxed < \left( \vec, \vec , \vec
Как вычислить смешанное произведение
Смешанное произведение можно обозначить еще одним способом:
Результат смешанного произведения – это число. Если число равно нулю, то векторы компланарны.
Как применять смешанное произведение
Если три вектора не компланарны, то на них, как на сторонах, можно построить параллелепипед, или пирамиду.
С помощью смешанного произведения можно рассчитывать объемы параллелепипедов или треугольных пирамид, построенных на трех некомпланарных векторах.
Примечание:
Определитель может быть равен отрицательному числу. А объем может быть либо нулевым, либо положительным. Поэтому, если при вычислении объема определитель будет равен отрицательному числу, знак минус не учитываем.
Рисунок 2 поясняет, как с помощью векторов на ребрах параллелепипеда можно рассчитать его объем
Рисунок 3 поясняет, как с помощью векторов на ребрах пирамиды можно рассчитать ее объем
Смешанное произведение векторов в физике — работа вращающей силы
Пусть цилиндрическое тело вращается под действием силы. Ось вращения проходит через ось симметрии тела.
Работа вращающей силы – это смешанное произведение векторов \( \vec <\omega>\), \(\vec < r>\) и \(\vec < F>\)
\[ \large \boxed < dA = \left( \vec
Пояснения:
Линейная скорость – это векторное произведение радиуса окружности на угловую скорость:
Расстояние, \( \vec
\[ \vec
Небольшая работа dA – это скалярное произведение вектора силы на вектор перемещения
\[ dA = \left( \vec
Компланарные векторы
Вы будете перенаправлены на Автор24
Понятие компланарности векторов
Для начала рассмотрим, какие вектора называются компланарными.
Два вектора, которые параллельны одной плоскости называются компланарными.
Для дальнейшего рассмотрения напомним следующую теорему.
Теоремы, связанные с условием компланарности трех векторов
Если один из трех данных векторов можно разложить по двум другим векторам, то есть
Доказательство.
Здесь возможны два случая.
Теорема доказана.
Готовые работы на аналогичную тему
Доказательство.
\[\overrightarrow
Причем это разложение единственно.
Которое также единственно.
Теорема доказана.
Признак и критерий компланарности векторов
Рисунок 1. Условие компланарности векторов. Автор24 — интернет-биржа студенческих работ
Пример задачи
Рисунок 2. Разложение по векторам. Автор24 — интернет-биржа студенческих работ
Решение.
Используя свойства сложения двух векторов, получим
Пусть нам дан параллелепипед. Найти тройки компланарных векторов, изображенных в параллелепипеде на рисунке ниже.
Рисунок 3. Параллелепипед. Автор24 — интернет-биржа студенческих работ
Решение.
Решение.
Применим признак компланарности трех векторов.
Рисунок 4. Нахождение определителя. Автор24 — интернет-биржа студенческих работ
Следовательно, это векторы компланарны, ч. т. д.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 27 04 2021