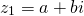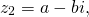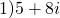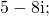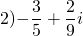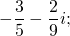Что значит число сопряженное к данному
Числа. Сопряженное число.
Сопряженное число: Если комплексное число 
, то число 
является сопряженным (либо комплексно сопряженным) к 
(часто обозначается как 
).
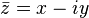
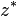
На комплексной плоскости сопряженные числа находят зеркально отражая их относительно вещественной оси. Модуль сопряженного числа равен модулю исходного числа, а аргументы сопряженных чисел имеют противоположные знаки.
Мнимая единица i из определения умножения имеет свойство того, что квадрат ее равняется –1, то есть она является квадратным корнем из –1.
Комплексное число –i обладает этим же свойством:
(–i) 2 = ((–1) 
i) 2 = (–1) 2 
i 2 = –1,
что естественно. Можно сказать, что некоторый 1-н квадратный корень из –1 обозначаем через i, тогда 2-й корень запишем как (–i). Замена i на (–i) приводит к понятию комплексного сопряжения.
Переход к сопряженному числу рассматривают еще как одноместную операцию. Перечислим ее свойства.
Свойства сопряженных чисел.
Еще некоторые соотношения:
Доказательство 
:
=a1a2 – b1b2 – (a1b2 + a2b1)i.
= (a1 – b1i)(a2 – b2i) =
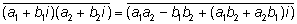
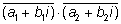
что и требовалось доказать.
Обобщим: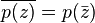 
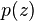
, где 
— произвольно взятый многочлен с вещественными коэффициентами. Отсюда видно, что у многочлена с вещественными коэффициентами есть или лишь действительные корни, или, если он имеет корни с не равной нулю мнимой частью, то они разбиваются на пары комплексно-сопряженных.
Умножение числителя и знаменателя комплексной дроби при комплексном знаменателе на сопряженное к знаменателю выражению используют для того, что бы избавиться от комплексности знаменателя. Это дает возможность выразить выражение в канонической форме комплексного числа или функции.
Значимость сопряжения объясняют тем, что оно есть образующей группы Галуа 
.
Комплексно сопряженные числа
Сопряженное (или комплексно сопряженное) число с комплексным числом \(\ z=x+i y \) является числом \(\ \overline
поиска для комплексного числа \(\ z=-34-i \) является его сопряженное число.
Следовательно, сопряженное число имеет вид: \(\ \overline
На комплексной плоскости сопряженные числа зеркалируются относительно оси действительных чисел.
Свойства комплексно-сопряженных чисел
1. \(\ |z|=|z| \), т. е. модули сопряженных чисел равны.
Модуль комплексного числа \(\ z=-4+i \) равен \(\ r=\sqrt<(-4)^<2>+1^<2>>=\sqrt <17>\). Присоединенным к комплексному числу является число \(\ z=-4-i \), модуль \(\ r=\sqrt<(-4)^<2>+(-1)^<2>>=\sqrt <17>\) которого равен модулю исходного числа.
2. \(\ \arg z=-\arg \overline
3. \(\ \overline<\overline
4. \(\ z \cdot \overline
5.\(\ z+\overline
6.\(\ \overline
7.\(\ \overline
Примеры решения проблем
Чтобы умножить комплексное число \(\ z=4-7 i \) на его сопряженное.
\(\ z \cdot \overline
Чтобы найти сопряженное к частному два комплексных числа: \(\ z 1=1-3 i \), \(\ z 2=2+5 i \).
Фактор комплексных чисел определяется путем умножения числителя и знаменателя на сопряженное число:
Мы получим тот же результат, если найдем фактор сопряженных чисел \(\ z \rceil=1-3 i \), \(\ z 2=2+5 i \):
Комплексно-сопряженные числа
Что такое комплексно-сопряженные числа? Как комплексно-сопряженные числа изображаются на комплексной плоскости?
у которых действительные части равны, а коэффициенты при мнимой части — противоположные числа, называются комплексно-сопряженными.
(другими словами, комплексонов-сопряженные числа — это комплексные числа, которые отличаются только знаком при мнимой части).
Примеры комплексно-сопряженных чисел:
Свойства комплексно сопряженных чисел
1) Действительное число является комплексно-сопряженным самому себе, так как a+0i=a-0i.
2) Сумма комплексно- сопряженных чисел — действительное число:
3) Разность комплексно-сопряженных чисел — мнимое число:
4) Произведение комплексно-сопряженных чисел — действительное число:
Изображение комплексно-сопряженных чисел на плоскости
На комплексной плоскости z1=a+bi и z2=a-bi изображаются
1) точками, симметричными относительно действительной оси ox.
Например, z1= — 6+3i и z2= — 6-3i; z3=0+2i и z4=0-2i; z5=5+0i и z6=5-0i.
2) векторами, симметричными относительно действительной оси ox.
Например, z1= 0+4i и z2= 0-4i; z3= 5+2i и z4= 5-2i; z5= — 6+0i и z6=- 6-0i.
Что значит число сопряженное к данному
Определение. Два комплексных числа, имеющие одну и ту же действительную часть и взаимно противоположные коэффициенты мнимых частей, называются 
взаимно) сопряженными.
Для любого комплексного числа z существует одно и только одно сопряженное с ним комплексное число, которое обозначается 
. Если 
, то 
. Очевидно, 
тогда и только тогда, когда z — действительное число.
Отметим, что сумма и произведение двух сопряженных комплексных чисел являются действительными числами:
Ранее было выведено правило деления комплексных чисел. Это правило можно проще получить с помощью сопряженных комплексных чисел.
Умножим числитель и знаменатель дроби — на число 
комплексно сопряженное со знаменателем. Выполнив действия и отделив действительную часть от мнимой, получаем:
Этот результат совпадает с формулой, полученной в п. 6.
Эту формулу можно не запоминать, а только помнить, что при делении надо числитель и знаменатель дроби умножить на число, комплексно сопряженное со знаменателем.
Теорема 1. Число, сопряженное с суммой или произведением комплексных чисел, есть сумма или соответственно произведение чисел, сопряженных данным комплексным числам:
Доказательство. Пусть 
. Тогда 
. Имеем:
Эта теорема показывает, что, поставив в соответствие каждому комплексному числу сопряженное с ним число, мы получили взаимно однозначное отображение поля комплексных чисел К на это же поле 
при котором сохраняются операции сложения и умножения.
Из теоремы 1 непосредственно вытекает следующее
Следствие 1. Число, сопряженное (натуральной) степени комплексного числа, равно той же степени числа, сопряженного данному:
Далее, если нам дан многочлен
коэффициенты которого — комплексные числа, то, заменив каждый коэффициент 
сопряженным ему комплексным числом 
мы получим новый многочлен, который обозначим через
Если теперь в полученном многочлене произвольное значение переменной 
заменить сопряженным ему значением 
то в силу доказанной выше теоремы и следствия I полученное значение многочлена 
будет комплексным числом, сопряженным с исходным значением многочлена 
Если, в частности, все коэффициенты 
многочлена 
действительные числа, то 
один и тот же многочлен, и формула (3) дает:
Таким образом, мы получили
Следствие 2. При замене в многочлене с действительными коэффициентами произвольного значения аргумента сопряженным ему числом значение многочлена также заменяется сопряженным ему числом.
Числа. Сопряженное число.
Сопряженное число: Если комплексное число , то число является сопряженным (либо комплексно сопряженным) к (часто обозначается как ).
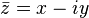
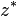
На комплексной плоскости сопряженные числа находят зеркально отражая их относительно вещественной оси. Модуль сопряженного числа равен модулю исходного числа, а аргументы сопряженных чисел имеют противоположные знаки.
Мнимая единица i из определения умножения имеет свойство того, что квадрат ее равняется –1, то есть она является квадратным корнем из –1.
Комплексное число –i обладает этим же свойством:
(–i) 2 = ((–1) i) 2 = (–1) 2 i 2 = –1,
что естественно. Можно сказать, что некоторый 1-н квадратный корень из –1 обозначаем через i, тогда 2-й корень запишем как (–i). Замена i на (–i) приводит к понятию комплексного сопряжения.
Переход к сопряженному числу рассматривают еще как одноместную операцию. Перечислим ее свойства.
Свойства сопряженных чисел.
Еще некоторые соотношения:
Доказательство :
=a1a2 – b1b2 – (a1b2 + a2b1)i.
= (a1 – b1i)(a2 – b2i) =
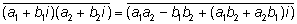
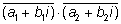
что и требовалось доказать.
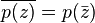
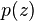
Обобщим: , где — произвольно взятый многочлен с вещественными коэффициентами. Отсюда видно, что у многочлена с вещественными коэффициентами есть или лишь действительные корни, или, если он имеет корни с не равной нулю мнимой частью, то они разбиваются на пары комплексно-сопряженных.
Умножение числителя и знаменателя комплексной дроби при комплексном знаменателе на сопряженное к знаменателю выражению используют для того, что бы избавиться от комплексности знаменателя. Это дает возможность выразить выражение в канонической форме комплексного числа или функции.
Значимость сопряжения объясняют тем, что оно есть образующей группы Галуа .