Что значит четная функция

Чётные и нечётные функции

Сегодня мы разберём:

1. Определение

Примеры чётных функций:

Примеры нечётных функций:

2. Исследование функции на чётность

Чтобы узнать, является функция чётной или нечётной (или вообще общего вида), нужны две проверки:

Главное, чтобы функция была задана формулой, а не таблицей, графиком или ещё как. Тогда исследование на чётность занимает несколько секунд. Мы сейчас убедимся в этом, но сначала важное замечание.

Примеры симметричных множеств:

Примеры несимметричных множеств:

Первые два множества несимметричны всего в одной точке (кстати, какой?). Но этого достаточно, чтобы прекратить исследование и отнести функцию к общему виду.

Разберём несколько примеров. Для начала — стандартный:

Исследуйте на чётность / нечётность функцию

А вот более хитрый случай:

Исследуйте на чётность / нечётность функцию

Область определения. Перед нами рациональная дробь. Её знаменатель должен быть отличен от нуля:

\[\begin 4-x & \ne 0 \\ x & \ne 4 \\ \end\]

Следовательно, область определения

Дальше попробуйте сами:

Исследуйте на чётность / нечётность функцию

Умение быстро определять чётность — чрезвычайно полезный навык. Особенно когда вы начнёте решать задачи с параметрами и всевозможные варианты ДВИ.

3. График чётной и нечётной функции

Всего два факта, которые нужно знать:

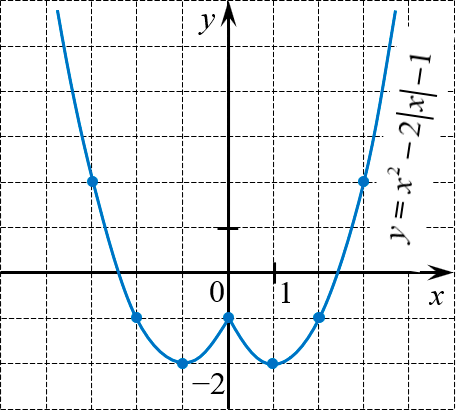
Ниже приведены графики нескольких чётных функций. Попробуйте построить их самостоятельно.

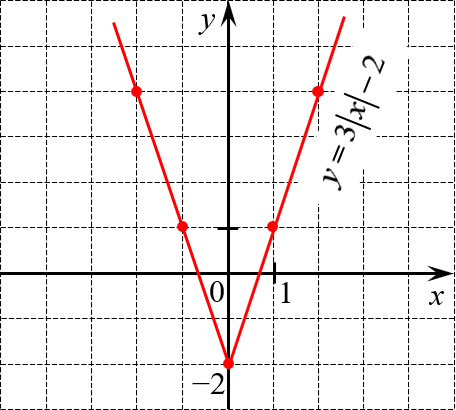
Постройте график функции

Постройте график функции

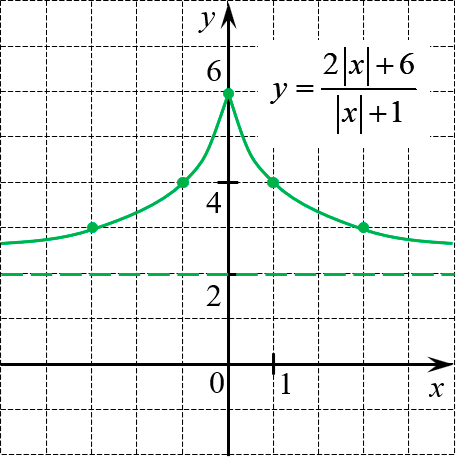
Это обычная гипербола, сдвинутая на 1 влево и на 2 вверх. Итого получим:

Обратите внимание на последний график. При всяком сдвиге и симметрии желательно показывать не только новое положение самого графика, но и положение всех ориентиров: вспомогательная система координат, вертикальные и горизонтальные асимптоты (особенно актуально для гипербол) и т.д.

Зачем всё это нужно? Исследование функции на чётность и нечётность незаменимо для решения сложных уравнений и задач с параметром:

4. Дополнение. Задачи с параметром

Чётность функций редко встречается сама по себе. Прежде всего это инструмент для решения сложных задач.

Задача решена. Ответы:

И ещё одна задача. Попробуйте решить её самостоятельно:

А чтобы действительно разобраться с чётностью, обязательно изучите ещё две темы:

После этого половина задач с параметром перестанет казаться вам сложными.:)

Источник

Понятие четной и нечетной функции

Понятие четности и нечетности функции

Главное условие при исследовании функции на четность/нечетность — это симметричность области определения относительно 0. Если она не симметрична, то функция не является ни четной, ни нечетной, и дальнейшее исследование производить не нужно. Например, \(D(y)\in(-\infty;+\infty)\) симметрична относительно 0, а \(D(y):x\in(-5;9)\) — нет.

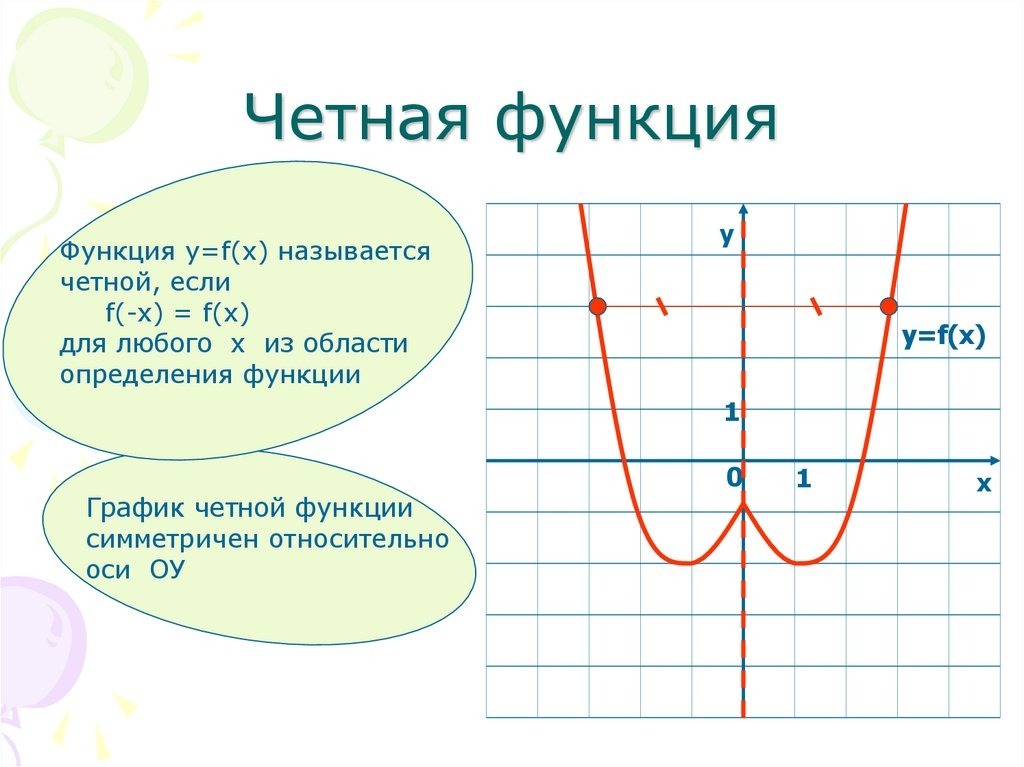
Четная функция

Функцию \(f(x)\) называют четной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=f(x).\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

График четной функции симметричен относительно оси Ох.

Нечетная функция

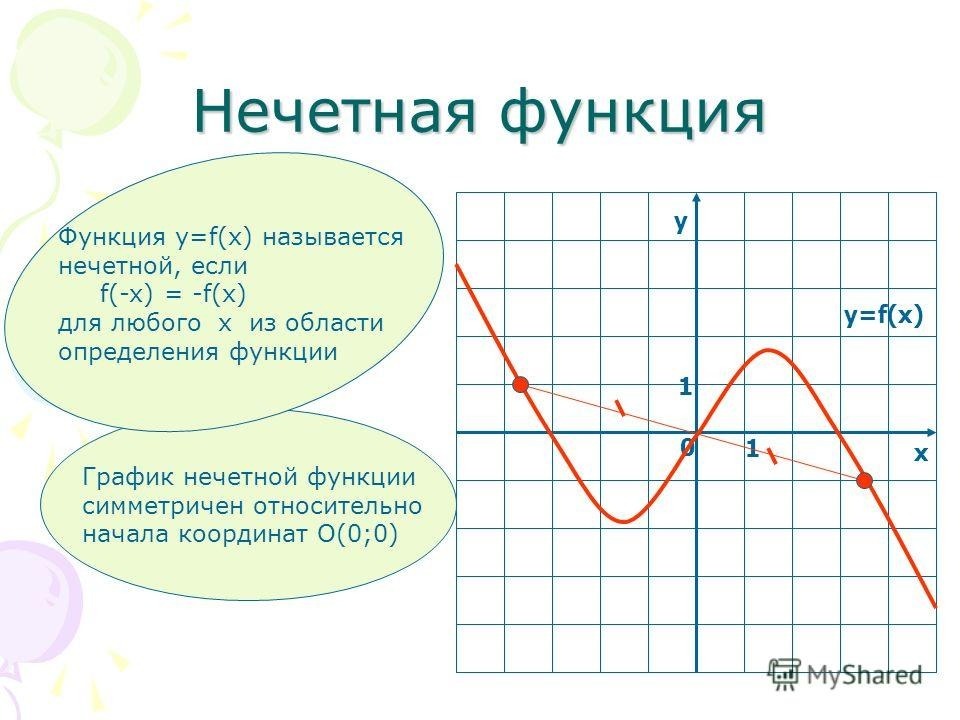
Функцию \(f(x)\) называют нечетной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=-f(x).\)

График нечетной функции симметричен относительно начала координат (точки (0;0)).

Произведение четной и нечетной функции

Произведение четной и нечетной функций есть нечетная функция.

Пусть \(f(x)\) — четная функция, а \(g(x)\) — нечетная. Тогда \(f(x)=f(-x), а g(-x)=-g(x).\)

Исследование функций в примерах

Доказать, что функция \(y=x^2\) четная.

1. Найдем область определения: \(D(y):x\in(-\infty;+\infty)\) — симметрична относительно 0.

Исследовать на четность и нечетность функцию \(f(x)=8x^3-7x.\)

1. Найдем область определения: \(D(f):x\in(-\infty;+\infty)\) — симметрична относительно 0.

Исследовать на четность и нечетность функции \(f_1(x)=\frac\) и \(f_2(x)=\frac4\)

Рассмотрим первую функцию:

1. Найдем область определения: x — любое число, кроме 1. Она не симметрична относительно 0, значит \( f_1(x)\) относится к функциям общего вида, то есть не является ни четной ни нечетной.

Рассмотрим вторую функцию:

Источник

Четные и нечетные функции

Вы будете перенаправлены на Автор24

Четные функции

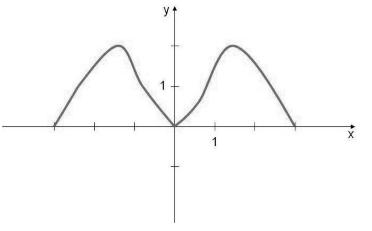
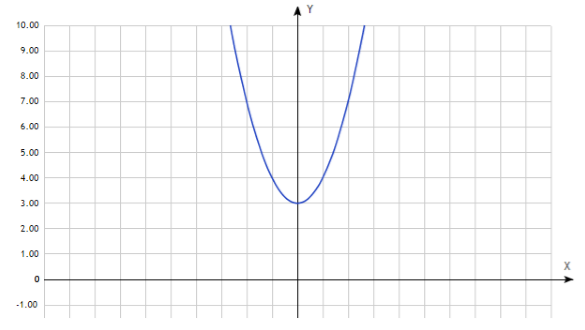
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).

Нечетные функции

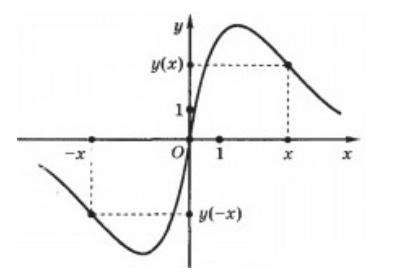
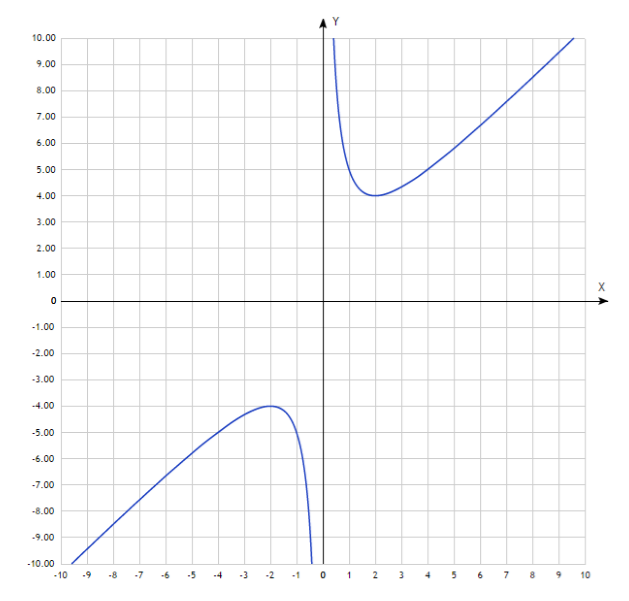
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).

Готовые работы на аналогичную тему

Функция общего вида

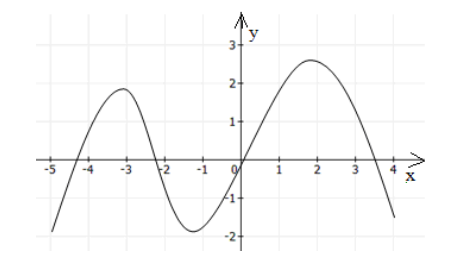
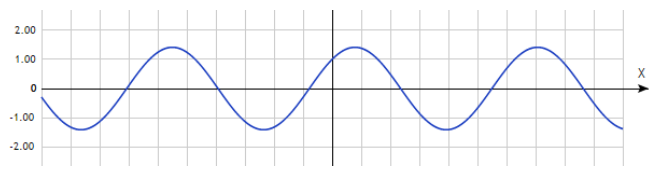
Функция общего вида никогда не будет симметрична оси ординат и началу координат. Пример функции общего вида изображен на рисунке 3.

Пример задачи

Исследовать функцию на четность и нечетность и построить их графики.

Изобразим её на графике:

Изобразим её на графике:

Изобразим её на графике:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 04 07 2021

Источник

Четность и нечетность функции

Определения и свойства четных и нечетных функций

\(\ f(x) \) называется четной функцией, если для любого x из области определения выполняется равенство \(\ f(-x)=f(x) \)

Функция \(\ f(x) \) называется нечетной функцией, если для любого x из области определения выполняется равенство \(\ f(-x)=-f(x) \)

Если ни одно из условий \(\ f(-x)=f(x) \) или \(\ f(-x)=-f(x) \) не выполняется, то говорят, что функция \(\ f(x) \) не является ни четной, ни нечетной (или функцией общего вида)

График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.

При исследовании функции на четность и нечетность можно использовать следующие свойства:

1.Сумма двух четных функций четна, а сумма двух нечетных функций нечетна.

2.Произведение двух четных функций является четной функцией, равно как и произведение двух нечетных функций. Произведение четной и нечетной функции — нечетная функция.

3.Если функция \(\ f(x) \) четная (нечетная), то и функция \(\ \frac<1> \) четная (нечетная).

Примеры решения задач

Используя определение исследовать на четность и нечетность следующие функции

1) Рассмотрим значение функции \(\ f_<1>(x)=2 x^<4>-3 x^<2>+6 \) в точке \(\ (-x) \) :

2) Найдем значение функции \(\ f_<2>(x)=8 x^<3>-7 x \) в точке \(\ (-x) \) :

Для этой функции выполняется условие \(\ f_<2>(-x)=-f_<2>(x) \),следовательно, она является нечетной.

3) Найдем значение функции \(\ f_<3>(x)=x^<4>-4 x+5 \) в точке \(\ (-x) \) :

2) \(\ f_<2>(x)=8 x^<3>-7 x \) — нечетная;

3) \(\ f_<3>(x)=x^<4>-4 x+5 \) — ни четная, ни нечетная.

Исследовать функцию \(\ f(x)=\frac+4><3 x^<6>+x^<4>+7> \) на четность, используя свойства четных и нечетных функций.

Исследуем отдельно четность функции, которые находятся в числителе и знаменателе:

то есть функция \(\ g(x) \) четная; аналогично

а тогда и функция \(\ h(x) \) четная.

Источник

Четность и нечетность функции. Период функции. Экстремумы функции

Содержание

Способы задания функции

Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.

Четная и нечетная функция

Функция является ни четной, ни нечетной и называется функцией общего вида, когда она не обладает симметрией относительно оси или начала координат.

Исследуем на четность нижеприведенную функцию:

Значит, функция f(x)=3x^<3>-7x^ <7>является нечетной.

Периодическая функция

f(x) > 0 на (x_<1>; x_<2>) \cup (x_<3>; +\infty )

f(x) на (-\infty; x_ <1>) \cup (x_<2>; x_ <3>)

Ограниченность функции

Возрастающая и убывающая функция

Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0 ).

а) Если при x > 0 четная функция возрастает, то убывает она при x

б) Когда при x > 0 четная функция убывает, то возрастает она при x

в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x

Экстремумы функции

Необходимое условие

Достаточное условие

Наибольшее и наименьшее значение функции на промежутке

Источник