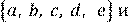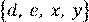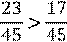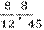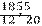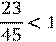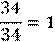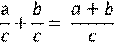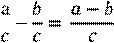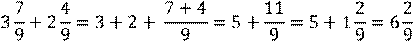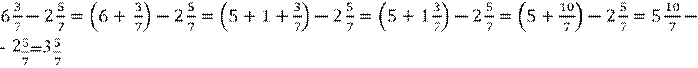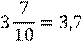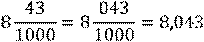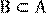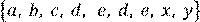Что такое wlp по математике 5 класс
Задания по математике 5 класс: для занятий дома
Самостоятельные занятия с ребенком в домашних условиях играют важную роль в процессе обучения. Даже не имея специального образования можно самостоятельно прорешивать с ним примеры и задачи по основным темам, встречающимся в текущем учебном году.
Эти задания вы можете распечатать на принтере.
§ Как правильно заниматься дома
Для того чтобы занятия действительно приносили пользу, необходимо придерживаться определенных правил, которые помогут сделать день продуктивнее, без утомления ребенка:
§ Задания для 5 класса на тему «Натуральные числа»
Перед тем как познакомиться с обыкновенными и десятичными дробями, необходимо вспомнить что такое натуральные числа. Ими называются числа, используемые в повседневной жизни, например для счета предметов.
✍ 3адание 1
Определить, какое число стоит перед:
Определить, какое число на две единицы больше, чем:
✍ 3адание 2
Написать в виде словосочетаний следующие цифры:
✍ 3адание 3
Представить в виде чисел словосочетания:
§ 3адания на тему «Сравнения натуральных чисел»
При помощи сравнения можно определить какое из чисел меньшее, а какое большее. Те что меньше, стоят при счете раньше, чем те, что больше.
✍ 3адание
Расставить 3наки « » или «=» между числами:
§ 3адания на тему «Сложение, вычитания натуральных чисел»
✍ 3адание 1
Для того чтобы повторить сложение, вычитание чисел, а также порядок действий при вычислении сложного выражения, можно решить несколько выражений:
Ответ: 1) 3 792, 2) 2 755, 3) 6 946, 4) 993.
✍ 3аданиие 2
В саду росло 208 фруктовых деревьев. Яблонь и слив было 129 штук, а слив и груш — 115. Сколько яблонь росло в саду? Слив? Груш?
Решение: Если известно, что всего деревьев было 208, а яблонь и слив – 129, то можно вычислить количество груш.
1 действие: 208 – 129 = 79 грушевых деревьев.
Стало известно количество грушевых деревьев, значит можно узнать, сколько было слив.
2 действие: 115 – 79 = 36 сливовых деревьев.
После того, как стало известно, сколько было груш и слив, можно высчитать количество яблонь.
3 действие: 208 – (79 + 36) = 93 яблонь.
Ответ: В саду росло 93 яблони, 79 груш и 36 слив.
§ 3адания на тему «Луч, прямая, отрезок»
Отрезком называется часть прямой ограниченная двумя точками, его длинной считается расстояние между крайними точками. Луч — это часть прямой, которая состоит из точки и всех других точек, лежащих по одну сторону от нее.
✍ 3адание 1
Начертите отрезок АВ, равный 12 см. Отметьте на нем точки по порядку С и D так, чтобы отрезок АС был равен 4 см, а СD — 6 см. Вычислите, чему равен отрезок DВ?
Ответ: 12 — (4 + 6) = 2 см.
✍ 3адание 2
Начертите произвольную прямую и отметьте на ней два точки А, В и С так, чтобы длина отрезка АВ была 7 см, а отрезка ВС — 4 см. Какова длина отрезка АС?
Ответ: 7 + 4 = 11 см.
§ 3адания на тему «Уравнения»
Уравнением называется равенство, в котором один или несколько компонентов являются неизвестными.
✍ 3адание 1
Решить уравнения
Ответ: 1) x=7, 2) х=6, 3) х=3, 4) х=-2,5, 5) х=5.
✍ 3адание 2
Насте 12 лет, что на 4 года меньше, чем возраста Лены. Сколько лет Лене? Решить уравнением.
Решение: Возьмем возраст Лены за x, в таком случае можно составить уравнение:
x – 4 = 12,
х = 12 + 4 = 16.
Ответ: Лене 16 лет.
✍ 3адание 3
Велосипедист за 3 дня проехал 117 км. Какое расстояние он преодолел в первый день, если в последующие два дня он проезжал на 4 км больше, чем в предыдущий? Какое расстояние он преодолел во 2-й и 3-й дни?
Решение: Расстояние которое проехал велосипедист за 1-й день, возьмем за x. В таком случае, второй день будет выглядеть как: x + 4, а третий: (х + 4) + 4.
Можно составить уравнение:
1 день 2 день 3 день
х + (х + 4) +( х + 4 + 4) = 117
3х + 12 = 117
3х = 117 – 12 = 105
х = 105: 3 = 35.
Проверка: 35 + 35 + 4 + 35 +4 + 4 = 117
Ответ: В первый день велосипедист проехал 35 км. Во 2-й день: 35 + 4 = 39 км. В 3-й день: 35 + 4 + 4 = 43 км.
§ 3адания на тему «Квадрат и куб числа»
Квадратом числа называется произведение этого числа самого на себя. Куб — произведение числа самого на себя два раза.
✍ 3адание 1
Найти квадрат чисел:
Ответ: 1) 25, 2) 81, 3) 169, 4) 2025, 5) 10 000, 6) 145 161.
Найти куб чисел:
Ответ: 1) 8, 2) 216, 3) 1 331, 4) 46 656, 5) 474 552, 6) 1 520 875.
✍ 3адание 2
Решить выражения:
Ответ: 1) 726, 2) 3 079, 3) 3 921, 4) 568, 5) 738, 6) 1 217.
§ 3адания на тему «Обыкновенные дроби»
✍ 3адание 1
1. Паша собрал 34 гриба, из которых 16 грибов оказались подосиновиками. Какую часть от всех грибов составляют подосиновики?
Ответ: 8/17.
2. Всего в книге 124 страниц, из которых Толя прочитал ровно половину. Какую часть книги прочитал Толя?
Ответ: 1/2.
3. Оля собрала всего 38 ягод, из которых 17 штук были малиной. Какую часть от общего количества составляют остальные ягоды?
✍ 3адание 2
Начертите отрезок и разделите его на 13 равных частей. Отметьте на данном отрезке: 3/13, 6/13, 10/13.
✍ 3адание 3
1. Полина собрала 36 листьев, из которых березовые составляют 6/18. Сколько березовых листьев собрала Полина?
Ответ: 12.
2. Папа был на рыбалке и поймал всего 45 рыбок, 8/15 было карасей. Сколько карасей поймал папа?
Ответ: 24.
3. Мама стряпала пирожки, всего их получилось 32 штуки. 5/8 от общего количества были с капустой. Сколько пирожков с капустой состряпала мама?
Ответ: 20.
✍ 3адание 4
Сравнить дроби:
§ 3адания на тему «Сложение и вычитание обыкновенных дробей»
✍ 3адание 1
Ответ: 1) 19/30, 2) 7/19, 3) 1/50, 4) 51/76, 5) 2/43.
✍ 3адание 2
Расстояние от дома до школы составляет 4/11 км, а от школы до магазина — 5/11 км. Чему равно расстояние от дома до магазина?
Решение: Для того чтобы найти сколько составляет весь путь, необходимо сложить расстояние от дома до школы и расстояние от школы до магазина 4/11 + 5/11 = 9/11 (км).
Ответ: Расстояние от дома до магазина составляет 9/11 км.
✍ 3адание 3
От рулона ткани первый раз отрезали 7/15 части, а затем еще 5/15, после чего в рулоне осталось 27 м. Сколько метров длина рулона?
Решение: В первую очередь нужно узнать какая часть рулона осталась.
1 действие: 15/15 — 7/15 — 5/15 = 3/15.
Можно сделать вывод, что 27 м составляет 3/15 части от всего рулона. Для того чтобы найти длину всего рулона ткани, необходимо узнать, сколько метров составляет 7/15 и 5/15 частей.
2 действие: 27 : 3 = 9 (м) — в 1 части.
3 действие: 9 • 7 = 63 (м) — составляет 7/15.
4 действие: 9 • 5 = 45 (м) — составляет 5/15.
После того, как стало известно какая длина у каждой из частей, можно вычислить всю длину рулона.
5 действие: 63 + 45 + 27 = 135 (м).
Ответ: длина рулона 135 метров.
§ 3адания на тему «Умножение и деление обыкновенных дробей»
✍ 3адание 1
Ответ: 1) 4/13, 2) 1/3, 3) 2/9, 4) 21/16, 5) 36/55.
✍ 3адание 2
В первом ящике лежит 3/16 от всего количества яблок, а во втором в 3 раза больше. Какая часть от всего количества яблок лежит в обоих ящиках?
Решение: Сначала нужно узнать сколько яблок лежит во втором ящике.
1 действие: 3/16 •3 = 9/16 (яб.).
После того как стало известно сколько яблок лежит во втором ящике, можно узнать их общее количество.
2 действие: 3/16 + 9/16 = 12/16 = 3/4 (яб.)
Ответ: 3/4 части от общего количества яблок лежит в обоих ящиках.
✍ 3адание 3
3а два дня автомобиль поехал 6/10 пути. Известно, что во второй день он проделал путь в 4 раза больше, чем в первый. Cколько проехал автомобиль в первый и второй день?
Решение: Пусть первый день пути будет x, тогда можно составить уравнение x + х • 4 = 6/10.
х + х • 4 = 6/10;
5 • x = 6/10;
х = 6/10 : 5;
х = 3/25 — проехал автомобиль в 1 день.
После того как стало известно, какая часть пути была преодолена в 1 день, можно высчитать 2 день.
2 действие: 3/25 • 4 = 12/25.
Ответ: в первый день автомобиль проехал 3/25, а во второй — 12/25.
§ 3адания на тему «Десятичные дроби»
✍ 3адание 1
Представить обыкновенные дроби в виде десятичных:
Ответ: 1) 0,5; 2) 0,13; 3) 0,2; 4) 0,164; 5) 0,18.
✍ 3адание 2
Начертите отрезок, разделите его на 6 равных частей. Отметьте на нем точки 0,3; 1,5; 2,2; 3,7; 4; 5,6.
§ 3адания на тему «Сложение и вычитание десятичных дробей»
✍ 3адание 1
Ответ: 1) 32,75; 2) 77; 3) 7,28; 4) 31,9; 5) 18,7; 6) 8,933.
✍ 3адание 2
В первый день катер проплыл 3,5 км, во второй на 4,31 км больше, а в третий — на 0,9 км меньше, чем во второй. Сколько всего км проплыл катер за 3 дня?
Решение: Необходимо вычислить, сколько катер проплыл в первый и во второй день.
1 действие: 3,5 + 4,31 = 7,81 (км) — проплыл во второй день.
2 действие: 7,81 — 0,9 = 6,91 (км) — проплыл в третий день.
После того как стало известно, сколько было пройдено за каждый день, можно узнать весь путь.
3 действие: 3,5 + 7,81 + 6,91 = 18,22 (км).
Ответ: за три дня катер проплыл 18,22 км.
§ 3адания на тему «Умножение и деление десятичных дробей»
✍ 3адание 1
Ответ: 1) 46,704; 2) 274,512; 3) 19,544; 4) 2,125; 5) 2,7; 6) 9,54.
✍ 3адание 2
3агадано число, если его увеличить в 3 раза, а затем прибавить 2,16, то получиться 27,96. Какое число было загадано?
Решение: Пусть неизвестное число будет x, тогда можно составить уравнение х • 3 + 2,16 = 27,96.
Ответ: было загадано число 8,6.
✍ 3адание 3
Расстояние между населенными пунктами равно 53,7 км. Навстречу друг другу вышли два пешехода, скорость первого 3,8 км/ч, второго — 4,6 км/ч. Какое расстояние будет между ними через 2,7 часа?
Решение: Нужно вычислить, какое расстояние пешеходы пройдут за 2,7 часа.
1 действие: 3,8 • 2,7 = 10,26 (км) — пройдет первый пешеход.
2 действие: 4,6 • 2,7 = 12,42 (км) — пройдет второй пешеход.
После того как стало известно, сколько прошли пешеходы, можно высчитать, какой путь им еще нужно преодолеть до встречи друг с другом.
3 действие: 53,5 — 10,26 — 12,42 = 30,82 (км).
Ответ: через 2,7 часа между пешеходами будет 30,82 км.
Определения и формулы метематика 5 класс Виленкин
Краткий курс математики 5 класс Виленкин.Поможет быстро повторить весь курс метематики 5 класса.
Просмотр содержимого документа
«Определения и формулы метематика 5 класс Виленкин»
Натуральные числа и шкалы.
Для счета применяют натуральные числа.
Последовательность всех натуральных чисел называют натуральным рядом.
Число можно записать с помощью десяти цифр: 0,1,2,3,4,5,6,7,8,9.Такую запись чисел называют десятичной.
Если запись натурального числа состоит из одного знака – одной цифры, то его называют однозначным.
Двузначные, трехзначные и т.д. числа называют многозначными.
Отрезок. Длина отрезка. Треугольник.
Прямая не имеет ни начала ни конца.
Через две точки можно провести только одну прямую.
Часть прямой ограниченная двумя точками называетя отрезком.
Луч- часть прямой ограниченная с одной стороны.
Числа соответствующие точкам на координатном луче называют координатами этих точек.
Точка с меньшей координатой лежит левее точки с больше координатой.
Сложение и вычитание натуральных чисел.
Сумма чисел не изменится при перестановке слагаемых.Это свойство сложения называют переместительным.
От прибавления нуля число не изменяется.
Сумму длин сторон многоугольника называют периметром этого многоугольника.
Числовые и буквенные выражения.
Буквенная запись свойств сложения и вычитания.
Переместительное свойство сложения записывают так: а+б=б+а. В этом равенстве буквы а и б могут принимать любые натуральные значения и значение 0.
Свойство нуля при сложении можно записать так: а+0=0+а=а. Здесь буква а может иметь любое значение.
Свойство вычитания суммы из числа записывают с помощью букв следующим образом: а- ( б+с)=а-б-с. Здесь б+с ≤ а.
Свойство вычитания числа из суммы записывают с помощью букв так: (а+б) – с = а+ ( б – с ), если с≤ б
Свойства нуля при вычитании можно записать так: а – 0 = а ; а – а = 0.
Умножение натуральных чисел и его свойства.
Произведение двух чисел не изменяется при перестановке множителей. Это свойство называют переместительным.С помощью букв его записывают так: а*б=б*а.
Ни одно число нельзя делить на нуль.
При делении любого числа на 1 получается это же число.
При делении числа на это же число получается 1.
При делении нуля на число получается нуль.
Порядок выполнения действий.
Сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел – действиями второй ступени.
а*а – квадрат числа; а*а*а- куб числа.
Отрезок. Длина отрезка. Треугольник.
Прямая не имеет ни начала ни конца.
Через две точки можно провести только одну прямую.
Часть прямой ограниченная двумя точками называетя отрезком.
Луч- часть прямой ограниченная с одной стороны.
Числа соответствующие точкам на координатном луче называют координатами этих точек.
Точка с меньшей координатой лежит левее точки с больше координатой.
Площади равных фигур равны. Их периметры тоже равны.
Площадь всей фигуры равна сумме площадей ее частей.
Квадрат – это прямоугольник с равными сторонами.
Для измерения площадей пользуются следующими единицами: кВ.мм., кВ.см., кВ.м., кВ. км.,
1 гектар –это площадь квадрата со стороной 100м.
1 ар ( сотка)-это квадрат со стороной 10м.
Поверхность прямоугольного параллелепипеда состоит из 6 прямоугольников.
Противоположные грани прямоугольного параллелепипеда равны.
Стороны граней называют ребрами параллелепипеда, а вершины граней – вершинами параллелепипеда.
Прямоугольный параллелепипед имеет 3 измерения – длину, ширину и высоту.
1 куб. дм. называют литром.
Замкнутая линия все точки которой лежат на одинаковом расстоянии от одной точки «О»,называется окружностью.
Точку «О» называют центром окружности и круга.
Отрезок соединяющий точку окружности с центром называют радиусом. Все радиусы одной окружности равны.
Часть окружности между двумя точками называют дугой окружности.
Доли. Обыкновенные дроби.
Две равные дроби обозначают одно и то же дробное число.
Правильная дробь меньше единицы, а неправильная больше или равна единице.
Смешанное число можно представить в виде неправильной дроби.
Равные десятичные дроби изображаются на координатном луче одной и той же точкой.
Десятичные дроби сравнивают по разрядам.
Приближенные значения чисел. Округление чисел
Замену числа ближайшим к нему натуральным числом или нулем называют округлением этого числа до целых.
Если первая отброшенная или замененная нулем цифра 5,6,7,8 или 9, то стоящую перед ней цифру увеличивают на единицу.
Если первая отброшенная или замененная нулем цифра 0,1,2,3 или 4, то стоящую перед ней цифру оставляют без изменения.
Умножение и деление десятичных дробей.
С помощью деления находят десятичную дробь, равную данной обыкновенной дроби.
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
Процентом называют одну сотую часть.
Два дополнительных друг другу луча образуют развернутый угол ( 180 гр.)
Прямым углом называют половину развернутого угла ( 90 гр.)
Градусом называют 1/180 часть развернутого угла.
Справочник по математике 5 класс.
ПРАВИЛА И ФОРМУЛЫ ЗА
учитель математики Истомина Т.Г.
ПРАВИЛА И ФОРМУЛЫ ЗА КУРС 5 КЛАССА
1. Натуральные числа
Числа, применяемые для счета, называются натуральными числами
Цифра нуль не относится к натуральным числам.
Однозначные числа: 1,2,3,4,5,6,7,8,9
Двузначные: 24,56,и т.д.
Трехзначные: 348,569 и т.д.
Многозначные: 23,562,456789 ит.д.
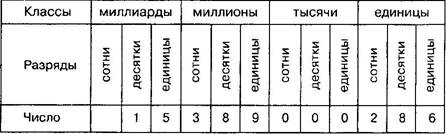
Разбиение числа на группы по 3 цифры, начиная справа, называется классами: первые
три цифры – класс единиц, следующие три цифры – класс тысяч, далее миллионы и т.д.
Отрезком называют линию, проведенную из точки А в точку В. Называют АВ или ВА
Длину отрезка АВ называют расстоянием между точками А и В.
Единицы измерения длины:
1) 10 см = 1 дм 2) 100 см = 1 м
3) 1 см = 10 мм 4) 1 км = 1000 м
Плоскость – это поверхность, которая не имеет краев, безгранично простирающаяся во всех направлениях.
Прямая не имеет начала и конца.
Две прямые, имеющие одну общую точку – пересекаются.
Луч – это часть прямой, которая имеет начало и не имеет конца (ОА и ОВ).
Лучи, на которые точка разбивает прямую, называют дополнительными друг другу.
О(0), Е(1), А(2), В(3) – координаты точек.
Из двух натуральных чисел меньше то, которое при счете называют раньше, и больше то, которое при счете называют позже. Единица – самое маленькое натуральное число.
Результат сравнения двух чисел записывают в виде неравенства: 5 368.
Число 8 меньше, чем 28 и больше, чем 5, можно записать в виде двойного неравенства:
На числовом луче обязательно указывают НАЧАЛО (0), ЕДИНИЧНЫЙ ОТРЕЗОК (1) и НАПРАВЛЕНИЕ (стрелочка с буквой х)
2. Сложение и вычитание натуральных чисел
Сложение
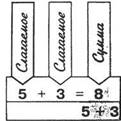
1. Переместительное свойство: Сумма чисел не изменяется при перестановке слагаемых: a + b = b + a (a и b – любые натуральные числа и 0)
2. Сочетательное свойство: Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме – второе слагаемое:
a + (b + с) = (a + b) +с = a + b + с (a, b и с – любые натуральные числа и 0).
3. Сложение с нулем: От прибавления нуля число не изменяется: а + 0 = 0 + а = a (a – любое натуральное число).
Сумму длин сторон многоугольника называют периметром этого многоугольника.
Вычитание
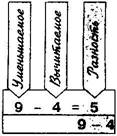
Число, из которого вычитают, называют уменьшаемым, число, которое вычитают, называют вычитаемым, результат вычитания называют разностью.
Разность двух чисел показывает, на сколько первое число больше второго или на сколько второе число меньше первого.
1. Свойство вычитания суммы из числа: Для того, чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а потом из полученной разности вычесть второе слагаемое:
3. Свойство вычитания нуля: Если из числа вычесть нуль, то оно не изменится:
a – 0 = a (a – любое натуральное число).
4. Свойство вычитания из числа этого же числа: Если из числа вычесть это число, получится нуль: a – a = 0 (a – любое натуральное число).
Числовые и буквенные выражения
Записи действий называют числовыми выражениями.
Число, получаемое в результате выполнения всех указанных действий, называют значением выражения.
Выражение, содержащее буквы называют буквенным выражением.
Числа, которыми заменяют букву, называют значениями этой буквы.
Уравнение
Уравнением называют равенство, содержащее букву, значение которой надо найти.
Значение буквы, при котором получается верное числовое равенство, называют корнем уравнения.
Решить уравнение – значит найти все его корни или убедиться, что их нет.
Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое:
Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность: а –27=43
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность:
3. Умножение и деление натуральных чисел
Умножение натуральных чисел и его свойства
Выражение m · n и значение этого выражения называют произведением чисел m и n. Числа m и n называют множителями.
1. Переместительное свойство умножения: Произведение двух чисел не изменяется при перестановке множителей: a · b = b · а
2. Сочетательное свойство умножения: Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель: a · (b · с) = (а · b) · c.
3. Свойство умножения на единицу: Сумма n слагаемых, каждое из которых равно 1, равна n: 1 · n = n.
4. Свойство умножения на ноль: Сумма n слагаемых, каждое из которых равно нулю,
равна нулю: 0 · n = 0.
Знак умножения можно опускать: 8 · х = 8х, или а · b = ab, или a · (b + с) = a(b + с)
Деление
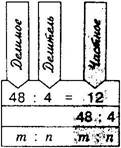
Действие, по которому по произведению и одному из множителей находят другой множитель, называют делением.
Число, которое делят, называют делимым; число, на которое делят, называют делителем, результат деления называют частным.
Частное показывает, во сколько раз делимое больше, чем делитель.
На нуль делить нельзя!
1. При делении любого числа на 1 получается это же число: а : 1 = а.
2. При делении числа на это же число, получается единица: а : а = 1.
3. При делении нуля на число получается нуль: 0 : а = 0.
Чтобы найти неизвестный множитель, надо произведение разделит на другой множитель. 5х = 45 х =45:5
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
48 : х = 4 х =48:4 х = 12
Деление с остатком
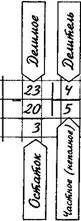
Здесь число 23 – делимое, 4 – делитель, 5 – неполное частное и 3 – остаток.
Если остаток равен нулю, то говорят, что делимое делится на делитель без остатка или, иначе, нацело.
Чтобы найти делимое a при делении с остатком, надо умножить неполное частное с на делитель b и к полученному произведению прибавить остаток d.
Упрощение выражений
1. Распределительное свойство умножения относительно сложения: Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения: (а + b)с = ас + bc.
2. Распределительное свойство умножения относительно вычитания: Чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе: (а — b)с = ас — bc.
3а + 7а = (3 + 7)а = 10а
10у = 85 – 25 10у = 60 у =60:10 у = 6 Ответ: 6
Порядок выполнения действий
Сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел – действиями второй ступени.
Правила порядка выполнения действий:
1. Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку слева направо.
2. Если выражение содержит действия первой и второй ступени и в нем нет скобок, то сначала выполняют действия второй ступени, потом – действия первой ступени.
3. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2).
Каждое выражение задает программу своего вычисления. Она состоит из команд.
Степень числа. Квадрат и куб числа
Произведение, в котором все множители равны друг другу, записывают короче:
а · а · а · а · а · а = а 6
Произведение n и n называют квадратом числа n и обозначают n 2 (эн в квадрате):
Произведение n · n · n называют кубом числа n и обозначают n 3 (эн в кубе):
Первая степень числа равна самому числу.
Если в числовое выражение входят степени чисел, то их значения вычисляют до выполнения остальных действий.
4. Площади и объемы
Формулы
Запись какого-нибудь правила с помощью букв называют формулой.
s = vt, где s – путь, v – скорость, t – время.
Площадь. Формула площади прямоугольника.
Чтобы найти площадь прямоугольника, надо его длину умножить на ширину.
S = ab, где S – это площадь, a – длина, b – ширина
Две фигуры называют равными, если одну из них можно наложить на вторую так, что эти фигуры совпадут.
Площади равных фигур равны.
Периметры равных фигур равны.

площади всего прямоугольника (см рисунок)
Квадрат – это прямоугольник с равными сторонами.
Площадь квадрата равна квадрату его стороны: S = a 2
Единицы измерения площадей
Квадратный миллиметр – мм 2
Квадратный сантиметр – см 2
Квадратный дециметр – дм 2
Квадратный километр – км 2
Площади полей измеряют в гектарах (га).
Гектар – это площадь квадрата со стороной 100 м.
Площади небольших участков земли измеряют в арах (а). Ар (сотка) – площадь квадрата со стороной 10 м.
1 м 2 = 100 дм 2 = 10 000 см 2
Если длина и ширина прямоугольника измерены в разных единицах, то их надо выразить в одних единицах для вычисления площади.
Прямоугольный параллелепипед
Поверхность прямоугольного параллелепипеда состоит из
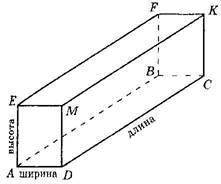
Противоположные грани прямоугольного параллелепипеда равны.
Стороны граней называют ребрами параллелепипеда, а вершины граней – вершинами параллелепипеда.
У прямоугольного параллелепипеда 12 ребер и 8 вершин.
Прямоугольный параллелепипед имеет три измерения длину, ширину и высоту (см. рис.)
Куб – это прямоугольный параллелепипед, у которого все измерения одинаковые.
Поверхность куба состоит из 6 равных квадратов.
Площадь поверхности прямоугольного параллелепипеда: S = (а• b + b • c + a • c) • 2
Площадь поверхности куба: S = 6• a 2
Объем прямоугольного параллелепипеда:
Чтобы найти объем прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту.
V = abc, V – объем, a длина, b – ширина, c – высота
Единицы измерения объемов:
Кубический миллиметр – мм 3
Кубический сантиметр – см 3
Кубический дециметр – дм 3
Кубический метр – мм 3
Кубический километр – км 3
1 м 3 = 1000 дм 3 = 1000 л
1 л = 1 дм 3 = 1000 см 3
1 км 3 = 1 000 000 000 м 3
5. Обыкновенные дроби
Окружность и круг
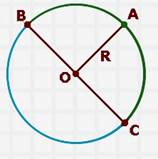
Часть плоскости, которая лежит внутри окружности называют кругом
Данная точка О – называется центром и круга, и окружности.
Отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности, называют радиусом окружности.
Отрезки OA, OB, и OC — это радиусы, их длины равны.
Отрезок, соединяющий две точки окружности и проходящий через ее центр, называют диаметром окружности.
Отрезок BC, проходящий через центр окружности (круга) называется диаметром и обозначается буквой d . Диаметр разделяет круг на два полукруга, а окружность на две
Диаметр равен двум радиусам, это хорошо видно на рисунке.
Доли. Обыкновенные дроби.
Запись вида 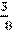
Знаменатель показывает, на сколько долей делят, а числитель – сколько таких долей взято.
Долю 
Долю 
Долю 
1 см = 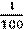
1 дм = 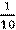
1 г = 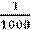
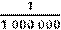
Сравнение дробей
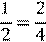
круга. Значит, круга равны круга. Поэтому
Из двух дробей с одинаковыми знаменателями меньше та, у которой меньше числитель, и больше та, у которой больше числитель.
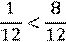
Правильные и неправильные дроби
Дробь, в которой чи слитель меньше знаменателя, называют правильной дробью.
Дробь, в которой числитель больше знаменателя или равен ему, называют неправильной
дробью.
Правильная дробь меньше единицы, а неправильная дробь больше или равна единице.
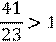
Сложение и вычитание дробей с одинаковыми знаменателями
При сложении дробей с одинаковыми знаменателями числители складывают, а
знаменатель оставляют тот же.
При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же.
Деление и дроби
Черту дроби можно принимать как знак деления:
Любое натуральное число можно записать в виде дроби с любым натуральным знаменателем. Числитель этой дроби равен произведению числа и этого
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные.
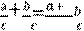
Смешанные числа


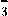

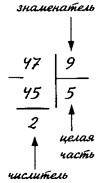
Чтобы из неправильной дроби выделить целую часть надо:
1) разделить с остатком числитель на знаменатель;
2) Неполное частное будет целой частью;
3) остаток (если он есть) дает числитель, а делитель – знаменатель дробной части.
Запись числа, содержащую целую и дробную части, называют смешанной.
Чтобы представить число в виде неправильной дроби, нужно:
1) умножить его целую часть на знаменатель дробной части;
2) 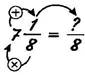
3) записать полученную сумму числителем дроби, а знаменатель дробной
части оставить без изменения.
Сложение и вычитание смешанных чисел
При сложении (и вычитании) чисел в смешанной записи целые числа складывают
(вычитают) отдельно, а дробные – отдельно.
Иногда при сложении смешанных чисел в их дробной части получается неправильная дробь. В этом случае из нее выделяют целую часть и добавляют ее к уже имеющейся целой части.
Если при вычитании смешанных чисел дробная часть уменьшаемого меньше дробной
части вычитаемого, поступают так:
6. Десятичные дроби. Сложение и вычитание десятичных дробей.
Десятичная запись дробных чисел
Числа со знаменателем 10, 100, 1000 и т.д. условились записывать без знаменателя в виде десятичной дроби.
Сначала пишут целую часть, а потом числитель дробной части. Целую часть отделяют от дробной части запятой.
Если дробь правильная, то перед запятой пишут цифру 0.
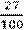
После запятой числитель дробной части должен иметь столько же цифр, сколько нулей в
Сравнение десятичных дробей
Если в конце десятичной дроби приписать нуль или отбросить нуль, то получится дробь, равная данной: 0,4560 = 0,456 = 0,45600; 45 = 45,0 = 45,00 и т.д.
Чтобы сравнить две десятичные дроби, надо сначала уравнять у них число десятичных знаков, приписав к одной из них справа нули, а потом, отбросив запятую, сравнить получившиеся натуральные числа.
Сравним: 8,367 и 8,39
Сложение и вычитание десятичных дробей
Чтобы сложить (вычесть) десятичные дроби, нужно:
1) уравнять в этих дробях количество знаков после запятой;
2) записать их друг под другом так, чтобы запятая была записана под запятой;
3) выполнить сложение (вычитание), не обращая внимания на запятую;
4) поставить в ответе запятую под запятой в данных дробях.
Запись: 0,6547 = 0,6 + 0,05 + 0,004 + 0,0007 называют разложением данного числа по разрядам.
Десятичные дроби можно сравнивать по разрядам.
Приближенные значения чисел. Округление чисел
При округлении чисел:
Если первая отброшенная или замененная нулем цифра равна 5, 6, 7, 8 или 9, то стоящую перед ней цифру увеличивают на 1.
Если первая отброшенная или замененная нулем цифра равна 0, 1, 2, 3 или 4, то стоящую перед ней цифру оставляют без изменения.
Округлим число до сотых:
Округлим число до тысячных:
7. Умножение и деление десятичных дробей
Умножение десятичных дробей на натуральные числа
Чтобы умножить десятичную дробь на натуральное число, надо:
1) 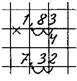
2) в полученном произведении отделить запятой столько цифр, сколько их отделено запятой в десятичной дроби.
Чтобы умножить десятичную дробь на 10,100, 1000 и т.д., надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.
8,5 · 1000 = 8,500 · 1000 = 8500
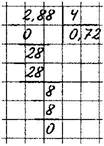
Деление десятичных дробей на натуральные числа
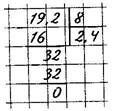
1) разделить дробь на это число, не обращая внимания на запятую;
2) поставить в частном запятую, когда кончится деление целой части.
Если целая часть меньше де лителя, то частное начинается с нуля целых.
Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д., надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.
56,378 : 100 = 0,56378
С помощью деления находят десятичную дробь, равную данной обыкновенной дроби.
Обратим дробь в десятичную:
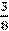
Умножение десятичных дробей
Умножить число на 0,1; 0,01; 0,001 и т.д. – то же самое, что разделить его на 10, 100, 1000 и т.д. Для этого надо перенести запятую влево на столько цифр, сколько нулей стоит перед единицей в множителе.
Чтобы перемножить две десятичные дроби, надо:
1) Выполнить умножение, не обращая внимания на запятые;
2) 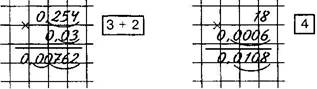
Если в произведении получается меньше цифр, чем надо отделить запятой, то впереди пишут нуль или несколько нулей.
При умножении числа на неправильную десятичную дробь оно увеличивается или не изменяется. При умножении числа на правильную десятичную дробь оно уменьшается.
Деление на десятичную дробь
Чтобы разделить число на десятичную дробь, надо:
1) в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе;
2) после этого выполнить деление на натуральное число.
При делении числа на неправильную дробь, это число уменьшается, а при делении на правильную дробь оно увеличивается.
Чтобы разделить десятичную дробь на 0,1; 0,01; 0,001 и т.д., надо перенести запятую вправо на столько цифр, сколько в делителе стоит нулей перед единицей (то есть умножить ее на 10, 100, 1000 и т.д.).
Если цифр не хватает, надо сначала приписать в конце дроби несколько нулей.
56,87 : 0,0001 = 56,8700 : 0,0001 = 568 700
Среднее арифметическое
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
Ср.ар. = (сумма чисел) : (количество слагаемых)
Сумма чисел = (среднее арифметическое) * (количество чисел)
Средняя скорость движения:
Средняя скорость = (Весь пройденный путь) : (все время движения)
Проценты
Процентом называют одну сотую часть. Процент обозначают знаком %.
Так как 1% равен сотой части величины, то вся величина равна 100%.
Чтобы обратить десятичную дробь в проценты, надо ее умножить на 100.
Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100.
Все решения задач на проценты делятся на три типа:
• нахождение процента от числа;
• нахождение числа по его проценту;
• сколько процентов одно число составляет от другого.
Чтобы найти процент от числа, надо:
1) выразить проценты обыкновенной или десятичной дробью; 2) умножить данное число на эту дробь.
Чтобы найти число по его проценту, надо:
1) выразить проценты обыкновенной или десятичной дробью; 2) разделить данное число на полученную дробь.
Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.
Угол. Прямой и развернутый угол. Чертежный треугольник
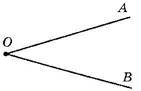
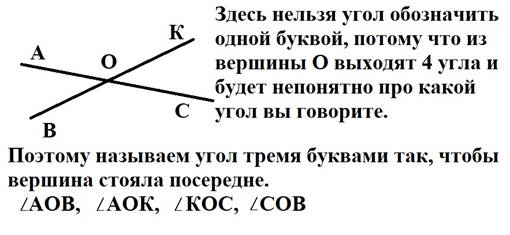
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой. ∠ АОВ или ∠ О
Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
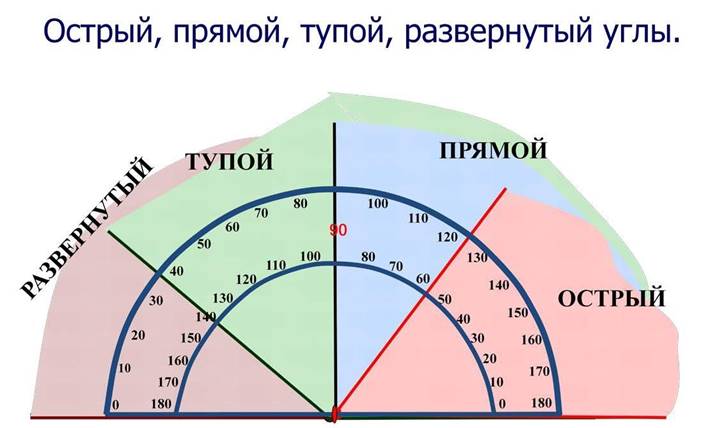
Два дополнительных друг другу луча образуют развернутый
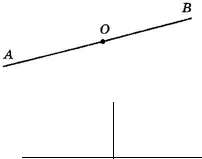
Прямым углом называют половину развернутого угла.
Значок угла нужно писать ПЕРЕД КАЖДЫМ углом, иначе получатся обозначение треугольника, а это грубая ошибка.
Помните, что стороны угла, биссектриса – это лучи, у них есть начало в вершине и нет конца. Луч обозначается двумя буквами, на 1 месте стоит вершина.
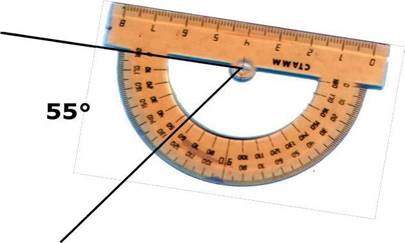
Измерение углов. Транспортир
Для измерения углов применяют транспортир.
Одно деление транспортира = 1° (один градус)
1° = / 180 РАЗВЕРНУТОГО УГЛА
Прямой угол равен 90 о
1. Совместить центр транспортира с вершиной угла.
2. Расположить транспортир таким образом, чтобы одна сторона угла проходила через начало отсчета
3. Выбрать соответствующую шкалу и определить, через какое деление проходит вторая сторона угла.
8. Множества. Операции над множествами.
Множества обозначают большими буквами латинского алфавита: А, В, С, D и т. д.
Объекты, составляющие множество, называются элементами множества.
Множество, которое не содержит ни одного элемента, называется пустым множеством и обозначается (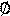
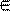
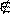
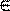
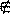
Знаки принадлежности множества множеству:
Если каждый элемент множества В является элементом множества А, то множество В называется подмножеством А. Если каждый элемент множества В принадлежит множеству А, то множество В является подмножеством множества А. Обозначение:
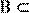
Обозначается :
Читается: множество B является подмножеством множества A.
Пересечением множеств А и В называется множество, в которое входят те и только те элементы, которые содержатся в А и В одновременно.
Если множества А и В не имеют общих элементов, т.е. эти два множества не пересекаются, тогда Ø
Объединением множеств А и В называется новое множество, состоящее из тех элементов, которые входят хотя бы в одно из множеств А или В. 
Например: N=