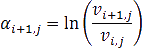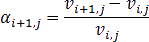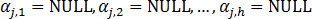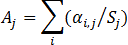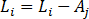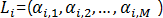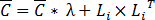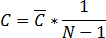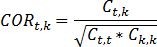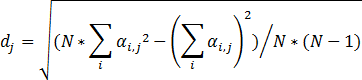Что такое value at risk
Value At Risk
Value at Risk (VaR) — стоимостная мера риска. Распространено общепринятое во всём мире обозначение «VaR». Это выраженная в денежных единицах оценка величины, которую не превысят ожидаемые в течение данного периода времени потери с заданной вероятностью. Также называется показателем «16:15», ибо именно в это время он должен был быть на столе у главы правления банка J.P.Morgan. В этом банке показатель VaR и был впервые введен в обиход с целью повышения эффективности работы с рисками.
VaR характеризуется тремя параметрами:
VaR — это величина убытков, которая с вероятностью, равной уровню доверия (например, 99%), не будет превышена. Следовательно, в 1% случаев убыток составит величину, большую чем VaR.
Проще говоря, вычисление величины VaR проводится с целью заключения утверждения подобного типа: “Мы уверены на X% (с вероятностью X/100), что наши потери не превысят Y долларов в течение следующих N дней”. В данном предложении неизвестная величина Y и есть VaR.
Бывает: 1) историческим, когда распределение доходностей берется из уже реализовавшегося временного ряда, то есть неявно предполагается, что доходности в будущем будут вести себя похожим на то, что уже наблюдалось, образом. 2) параметрическим, когда расчеты проводятся в предположении, что известен вид распределения доходностей (чаще всего оно предполагается нормальным).
Содержание
Альтернативные методики расчета риска
Формула расчета ожидаемых убытков
Вычисление параметрического VaR
(i)
(ii)
Предположение о нормальности распределения доходностей позволяет нам вычислить z-уровень для данного доверительного уровня, так для 95% доверительного уровня имеем:
VaR в управлении рисками
Вычисление рисков методом Value at Risk

Последние десятилетия мировая экономика регулярно попадает в водоворот финансовых кризисов. 1987, 1997, 2008 чуть не привели к коллапсу существующей финансовой системы, именно поэтому ведущие специалисты начали разрабатывать методы, с помощью можно контролировать неопределенность, господствующую в финансовом мире. В Нобелевских премиях последних лет (полученных за модель Блэка-Шоулза, VaR, и т.д.) отчетливо прослеживается тенденция к математическому моделированию экономических процессов, попыткам предсказать поведение рынка и оценить его устойчивость.
Сегодня я постараюсь рассказать о наиболее широко применяемой методике предсказаний потерь — Value at Risk (VaR).
Понятие VaR
Методы расчета VaR
Историческое моделирование
При историческом моделировании мы берем уже известные из прошлых измерений значения финансовых колебаний для портфеля. К примеру, у нас есть поведение портфеля на протяжении предыдущих 200 дней, на основе которых мы решаем вычислить VaR. Предположим, что на следующий день финансовый портфель будет вести себя также, как в один из предыдущих дней. Таким образом, мы получим 200 исходов на следующий день. Далее, мы допускаем, что случайная величина распределена по нормальному закону, основываясь на этом факте, мы понимаем, что VaR — это один из перцентилей нормального распределения. В зависимости от того, какой уровень допустимого риска мы взяли, выбираем соответствующий перцентиль и, как следствие, получаем интересующие нас значение.
Недостатком этого метода является невозможность построения предсказаний по портфелям, о которых у нас нет сведений. Также может возникнуть проблема, в случае, если составляющие портфеля существенно изменятся за короткий промежуток времени.
Хороший пример вычислений можно найти по следующей ссылке.
Метод ведущих компонент
Для каждого финансового портфеля можно вычислить набор характеристик, помогающих оценить потенциал активов. Эти характеристики называются ведущими компонентами и, обычно, представляют собой набор частных производных от цены портфеля. Для вычисления стоимости портфеля обычно используется модель Блэка — Шоулза, о которой я постараюсь рассказать в следующий раз. В двух словах, модель представляет собой зависимость оценки европейского опциона от времени и от его текущей стоимости. Основываясь на поведении модели мы можем оценить потенциал опциона, анализируя функцию классическими методами математического анализа (выпуклость/вогнутость, промежутки возрастания/убывания и т.д.). Базируясь на данных анализа, VaR рассчитываются для каждой из компонент и результирующее значение строиться, как комбинация (обычно взвешенная сумма) каждой из оценок.
Метод Монте-Карло
Метод Монте-Карло во многом похож на метод исторического моделирования, разница в том, что вычисление производится не на основе реальных данных, а на случайно сгенерированных значениях. Преимуществом такого метода является возможность рассмотрения, как большого числа ситуаций, так и эмулирование поведения рынка в экстремальных условиях. Явным недостатком являются большие вычислительные ресурсы, требуемые для реализации такого подхода. При работе с этой методикой обычно используются NoSQL хранилища и распределенные вычисления на базе MapReduce. Хороший пример использования Hadoop для вычисления VaR можно найти по следующей ссылке.
Естественно, это не единственные методики вычисления VaR. Существуют как простые линейные и квадратичные модели предсказания цены, так и достаточно сложный метод вариаций-ковариаций, о которых я не рассказал, но интересующиеся смогут найти описание методик в нижеприведенных книгах.
Критика методики
Важно отметить, что при подсчете VaR принимается гипотеза о нормальном поведении рынка, однако, если бы это допущение было верным, крисизы случались бы раз в семь тысяч лет, но, как мы видим, это абсолютно не верно. Нассим Талеб, известный трейдер и математик, в книгах «Одураченные случайностью» и «Черный лебедь» подвергает существующую систему оценки рисков жесткой критике, а также предлагает свое решение, в виде использования другой системы расчета рисков, базирующейся на логонормальном распределении.
Несмотря на критику, VaR вполне успешно используется во всех крупнейших финансовых институтах. Стоит отметить, что данный подход не всегда применим, в силу чего, были созданы другие методики со схожей идеей, но другим методом расчета (например, SVA).
С учетом критики были разработаны модификации VaR, основанные либо на других распределениях, либо на других методиках расчетов на пике Гауссовой кривой. Но об этом я постараюсь рассказать уже в другой раз.
Value-At-Risk
Сутью VaR является четкий и однозначный ответ на вопрос: какой максимальный убыток рискует понести инвестор за определенный период времени с заданной вероятностью? Отсюда следует, что величина VaR определяется как наибольший ожидаемый убыток, который с заданной вероятностью может получить инвестор в течение n дней.
Ключевыми параметрами VaR является период времени, на который производится расчет риска, и заданная вероятность того, что потери не превысят определенной величины. Например, стандартом для брокерско-дилерских отчетов по операциям с внебиржевыми производными инструментами, передаваемым в Комиссию по биржам и ценным бумагам США, являются 2-недельный период и 99%-вероятность. The Bank of International Settlements для оценки достаточности банковского капитала установил вероятность на уровне 99% и период, равный 10 дням. JP Morgan опубликовывает свои дневные значения VaR при 95% доверительном уровне.
VaR является универсальной методикой расчета различных видов риска:
При расчете на вход подаются две матрицы:
дата. Включает дату расчета и даты, входящие в период ретроспективы. Измерение не должно содержать пропусков, начиная от расчетной даты и заканчивая последней датой из ретроспективы;
Перед расчетом VaR необходимо рассчитать следующие величины:
стандартные отклонения по выборке.
Если используется заполнение пропусков, то производится проверка матрицы финансовых инструментов на наличие пустых значений (Null). Проверка проводится с первой даты ретроспективы до расчетной даты по каждому финансовому инструменту. Если встречается значение Null, то вместо него устанавливается первое непустое значение за предыдущую дату, входящую в период ретроспективы, если за предыдущие периоды все значения являются пустыми, то значение остается пустым.
Для каждого финансового инструмента производится расчет доходности на расчетную дату и на весь период ретроспективы, начиная с даты после первой даты в периоде, через количество дней, указанных в качестве временного горизонта. Если используется логарифмическая доходность, то расчет производится по формуле:
Если логарифмическая доходность не используется, то по формуле:
i = 1. Самая младшая дата в периоде;
i = h + 1. Дата, наступающая через h дней после первой даты в периоде;
Для всех финансовых инструментов:
На основе полученной матрицы доходности считается матрица корреляций. Если не используется гипотеза о нулевом среднем, то считается среднее значение за весь период отмеченных дат для каждого финансового инструмента (пустые значения не учитываются):
Далее из каждой строки матрицы доходности вычитается вектор средних значений, по правилам вычитания матриц:
Для расчета матрицы корреляций считается матрица ковариаций по формуле:
Матрица корреляции считается по формуле:
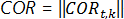
Для каждого финансового инструмента рассчитывается среднее значение (пустые значения не учитываются) и стандартное отклонение по выборке. Источником данных является матрица доходности.


Формула расчета стандартного отклонения по выборке:
Условная стоимость под риском (CVaR)
Опубликовано 17.07.2021 · Обновлено 17.07.2021
Что такое Условная стоимость под риском (CVaR)?
Условная стоимость под риском (CVaR), также известная как ожидаемый дефицит, представляет собой меру оценки риска, которая количественно определяет величину остаточного риска инвестиционного портфеля. CVaR рассчитывается путем взятия средневзвешенного значения «экстремальных» убытков в хвосте распределения возможных прибылей, превышающих точку отсечения значения, подверженного риску (VaR). Условная стоимость под риском используется при оптимизации портфеля для эффективного управления рисками.
Ключевые моменты
Понимание условной стоимости под риском (CVaR)
Вообще говоря, если инвестиция показала стабильность с течением времени, то рисковая стоимость может быть достаточной для управления рисками в портфеле, содержащем эту инвестицию. Однако чем менее стабильны инвестиции, тем больше вероятность того, что VaR не даст полной картины рисков, поскольку он безразличен ко всему, что выходит за пределы своего собственного порога.
Условная стоимость под риском (CVaR) пытается устранить недостатки модели VaR, которая представляет собой статистический метод, используемый для измерения уровня финансового риска внутри фирмы или инвестиционного портфеля в течение определенного периода времени. В то время как VaR представляет собой убыток наихудшего случая, связанный с вероятностью и временным горизонтом, CVaR – это ожидаемые убытки, если этот порог наихудшего случая когда-либо будет пересечен. CVaR, другими словами, количественно определяет ожидаемые потери, которые происходят после точки останова VaR.
Формула условной стоимости под риском (CVaR)
CVарзнак равно11-c∫-1VарИксп(Икс)dИксжчере:п(Икс)dИксзнак равнотче ртоббялятYденсекятуойгеттянггетурншятч валуе «Икс”cзнак равнотче сут-охе роянт он тче дIсекттябутIон шчеRх TченлYсект ыеты тче Vар бреакпоинтVарзнак равнотчеггеед-урон Vар левел\ begin
Условная стоимость под риском и инвестиционные профили
Более безопасные инвестиции, такие как акции США с большой капитализацией или облигации инвестиционного уровня, редко превышают VaR на значительную величину. Более волатильные классы активов, такие как акции компаний с малой капитализацией в США, акции развивающихся рынков или деривативы, могут иметь CVaR, во много раз превышающие VaR. В идеале инвесторы ищут небольшие CVaR. Однако инвестиции с наибольшим потенциалом роста часто имеют большие CVaR.
Финансово-инженерные инвестиции часто сильно зависят от VaR, потому что он не увяз в выбросах данных в моделях. Однако были времена, когда разработанные продукты или модели могли быть лучше сконструированы и более осторожно использовались, если бы предпочтение было отдано CVaR. История знает множество примеров, таких как управление долгосрочным капиталом, которое зависело от VaR для измерения своего профиля риска, но все же сумело сокрушить себя, не приняв во внимание убыток, превышающий прогнозируемый моделью VaR. В этом случае CVaR сфокусировала бы хедж-фонд на истинной подверженности риску, а не на отсечении VaR. В финансовом моделировании почти всегда ведутся споры о сравнении VaR и CVaR для эффективного управления рисками.
Методы оценки риска VaR (Value at Risk). Рыночный риск. Пример расчета в Excel
Рассмотрим методы оценки риска, в частности рыночного, с помощью меры риска VaR (Value at Risk). Для этого разберем практический пример оценки риска для акции компании ОАО «Газпром».
Рыночный риск. Определение
Рыночный риск (англ. Market risk) – это вероятность неблагоприятного изменения стоимости активов. На изменение стоимости влияют множество макро-, мезо-, микроэкономических факторов, к которым можно отнести цены на сырье (нефть, сталь, платина и т.д.); цены на драгоценные металлы (золото, серебро); изменения отраслевых индексов производства, национальных показателей (ВВП, безработица, ключевая процентная ставка, инфляция), уровня спроса и предложения и т.д.
Рыночные риски находятся в системе финансовых рисков и можно выделить их следующие виды:
Рыночные риски оценивают различные инвестиционные компании, инвестиционные и хеджевые фонды, частные инвесторы, банки, предприятия, финансовые агенты, поставщики и т.д. для минимизации возможных убытков и создания резервов. Как мы видим, рыночные риски влияют на самых различных участников финансового рынка.
 | ★ Excel таблица для формирования инвестиционного портфеля ценных бумаг (рассчитай портфель за 1 минуту) + оценка риска и доходности |
 | ★ Программа InvestRatio — расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса |
Оценка стоимости бизнеса | Финансовый анализ по МСФО | Финансовый анализ по РСБУ |
Расчет NPV, IRR в Excel | Оценка акций и облигаций |
Методы оценки риска
Для того чтобы управлять возможными потерями и определять резервы для страхования потерь необходима количественная оценка риска. Основная аксиома любого управления заключается в том, что управлять можно только тем, что можно количественно измерить. Все методы оценки рыночных риском можно условно разделить на две группы:
К преимуществам статистических методов можно отнести возможность объективной оценки вероятности возникновения непредвиденных убытков и их абсолютного размера. Экспертные методы оценки позволяют учесть слабоформализуемые факторы риска и разработать различные сценарии его снижения.
Г.Марковиц в начале 60-х годов предложил оценивать риск как изменчивость стоимости ценных бумаг на фондовом рынке. То есть чем сильнее изменяется цена актива, тем выше риск вложения в него. Недостатками данного способа были в неспособности спрогнозировать размер и вероятность будущих убытков.
Метод оценки рыночного риска. Мера риска VaR (Value at Risk). Что такое VaR?
В 80-е годы был предложен новый критерий риска – VaR (Value at Risk), который позволил комплексно оценить возможные убытки в будущем с выбранной вероятностью и за определенный промежуток времени. Для расчета меры риска VaR на практике используют несколько способов:
Оценка риска по методу VaR на основе исторического моделирования в Excel
Рассмотрим пример оценки риска актива на фондовом рынке по модели VaR на основе дельта нормального моделирования вероятности и размера убытка. Возьмем котировки акции ОАО «Газпром» и рассчитаем возможные убытки по данному виду актива. Для этого необходимо закачать котировки с сервиса finam.ru («Экспорт данных») или с сайта finance.yahoo.com, если вы будете оценивать рыночный риск для иностранных компаний. По рекомендации Bank of International Settlements для расчета VaR необходимо использовать не менее 250 данных по стоимости акции. Были взяты дневные котировки по ОАО «Газпром» за период 31.01.2014 – 31.01.2015.
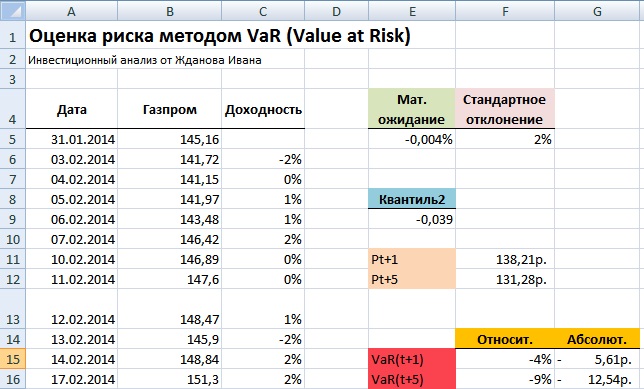
Оценка рыночного риска методом Value at Risk (VaR)
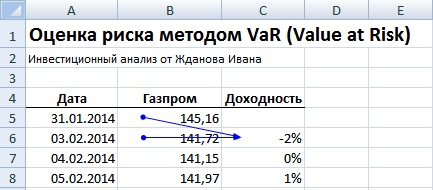
На следующем этапе необходимо рассчитать дневную доходность акции ОАО «Газпром», воспользовавшись следующей формулой.
Доходность акции ОАО «Газпром» =LN(B6/B5)
Расчет доходности акции ОАО «Газпром»
Следует отметить, что корректность использования дельта нормального метода оценки риска достигается только при подчинении факторов риска (доходности) нормальному закону распределения (Гауссовому). Для определения принадлежности распределения доходности Гауссовому распределению можно воспользоваться классическими статистическими критериями – Коломогорова-Смирнова или Пирсона.
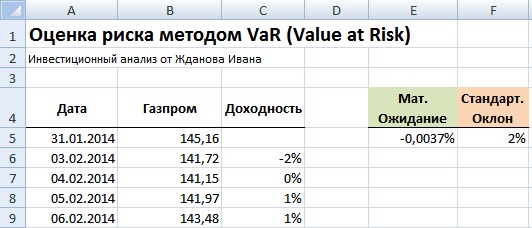
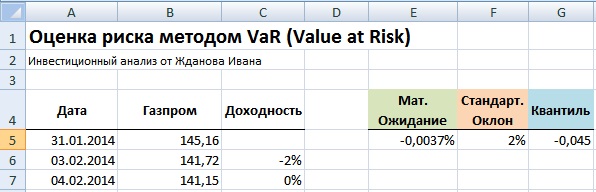
На следующем шаге необходимо рассчитать основные параметры распределения доходности: математическое ожидание и стандартное отклонение. Для этого воспользуемся встроенными формулами в Excel:
Математическое ожидание =СРЗНАЧ(C5:C255)
Стандартное отклонение =СТАНДОТКЛОН(C5:C255)
Расчет параметров функции распределения доходностей акции
Следующим этапом в расчете меры риска VaR является определение квантиля данного нормального распределения. В статистике под квантилем понимают – значение функции распределения (Гаусса) по заданным параметрам (математического ожидания и стандартного отклонения) при которых функция не превышает данное значение с заданной вероятностью. В нашем примере уровень вероятности был взят 99%.
Оценка квантиля в Excel
Прогнозирование будущей стоимости акции на основе метода VaR
Далее необходимо оценить какой возможно будет стоимость акции при заданных параметрах распределения доходности. Для этого можно воспользоваться следующей формулой:
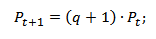
q – квантиль распределения доходностей акции;
Pt – стоимость акции в момент времени t;
Pt+1 – минимальная стоимость акции в следующем периоде времени t с заданным уровнем квантиля.
Для прогнозирования будущей стоимости акции (актива) на несколько периодов вперед следует использовать модификацию формулы:
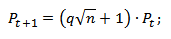
q – квантиль распределения доходностей акции;
Pt – стоимость акции в момент времени t;
Pt+1 – минимальная стоимость акции в следующем периоде времени t при заданном уровне квантиля;
n – глубина прогноза возможной минимальной стоимости акции.
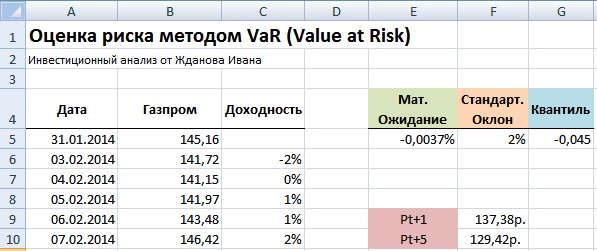
Формула расчета будущей стоимости акции в Excel будет иметь вид:
Минимальная стоимость акции ОАО «Газпром» на следующий день =(1+G5)*B255
Минимальная стоимость акции ОАО «Газпром» через 5 дней =B255*(1+G5*КОРЕНЬ(5))
Прогнозирование минимальной стоимости акции с заданной вероятностью
Значения Pt+1 показывает, что с вероятностью 99% акции ОАО «Газпром» не опустятся ниже цены равной 137.38руб, а значение Pt+5 показывает возможную минимальную стоимость акции с вероятностью 99% на 5 следующих дней. Для расчета абсолютного значения возможного убытка следует определить процентное изменение стоимости акции. Формулы расчета в Excel будут следующие:
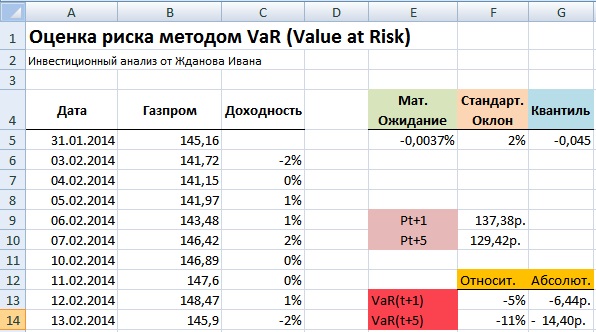
Относительное изменение стоимости акции
Относительное снижение стоимости акции на следующий день =LN(F9/B255)
Относительное снижение стоимости акции за пять дней =LN(F10/B255)
Абсолютное изменение стоимости акции
Абсолютное снижение стоимости акции на следующий день =F9-B255
Абсолютное снижение стоимости акции за пять дней =F10-B255
 | ★ Программа InvestRatio — расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса |
Таким образом читать экономический смысл показателя VaR заключается в следующем: в течение следующего дня стоимость акции ОАО «Газпром» с вероятностью 99% не окажется ниже 137,38руб. и абсолютные убытки не превысят 6,44руб (5%) на акцию. И аналогично для оценки VaR на пять дней вперед: в течение пяти дней стоимость акции ОАО «Газпром» с вероятностью 99% не опуститься ниже 129,42 руб., и потеря капитала не превысит 11% (14,4руб на акцию).
Мера риска VaR. Пример расчета в Excel
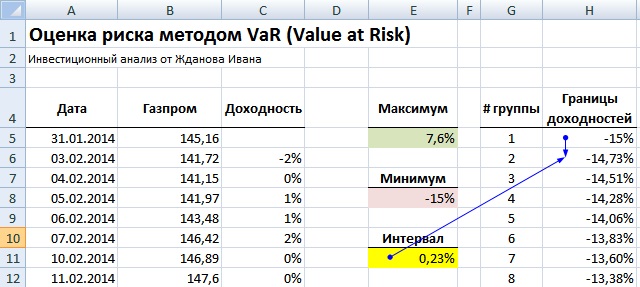
Оценка меры риска VaR на основе «ручного способа» в Excel
Второй метод расчета меры риска VaR называется «ручным способом», так как позволяет не привязываться к распределению, по которому изменяется стоимость актива. Это одно из его главных преимуществ по отношению к дельта нормальному методу. Для оценки рыночного рискам будем использовать те же входные данные – котировки ОАО «Газпром». Этапы расчета VaR следующие:
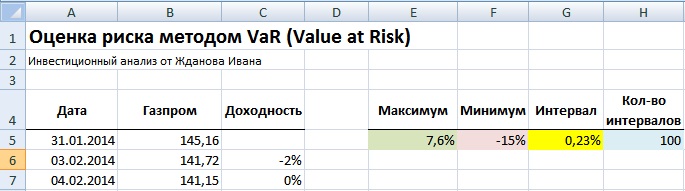
Расчет максимума и минимума доходностей акции ОАО «Газпром»
По рассчитанной доходности акции ОАО «Газпром» определяем максимум и минимум доходности. Для этого воспользуемся формулами:
Максимальное значение доходности акции =МАКС(C5:C255)
Минимальное значение доходности акции =МИН(C5:C255)
Выбор количества интервалов группировки доходностей/убытков акции
Для ручного способа оценки риска необходимо взять количество интервалов деления группировки доходностей. Количество может быть любое, в нашем примере мы возьмем N=100.
Определение ширины интервала группировки доходностей
Ширина интервала или шаг изменения группы необходим для построения гистограммы и рассчитывается как деление максимального разброса доходностей к количеству интервалов. Формула расчета интервала следующая:
Размер интервала доходностей акции =(E5-F5)/H5
Оценка меры риска VaR «ручным способом»
На следующем этапе необходимо построить гистограмму распределения доходностей по выбранным интервалам. Для этого рассчитываем границы всех групп доходностей (всего их 100). Формула расчета следующая:
Граница доходностей акции =H5+$E$11
Расчет границы доходностей в Excel для акции ОАО «Газпром»
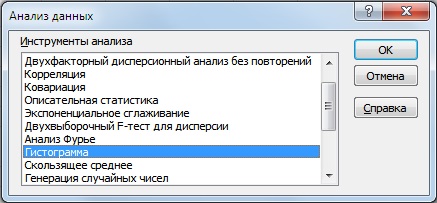
После определения границ групп доходностей строим накопительную гистограмму. Для этого заходим в надстройку «Данные» → «Анализ данных» → «Гистограмма».
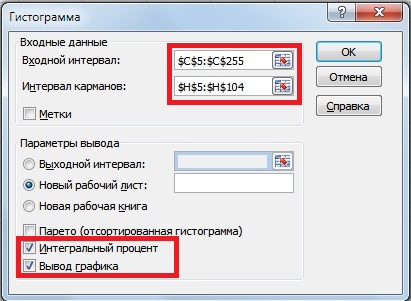
В открывшемся окне заполняем «Входные интервалы», «Интервалы карманов», также выбираем опцию «Интегральный процент» и «Вывод графика».
Пример построения гистограммы доходностей ОАО «Газпром»
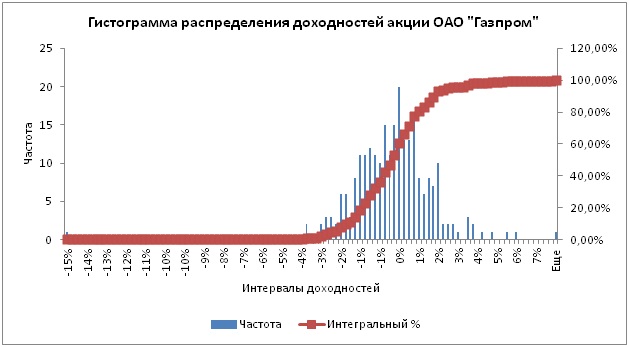
В результате будет сформирован новый рабочий лист с графиком и частотой попадания доходности/убытка в тот или иной интервал. График накопительным итогом имеет следующий вид:
Гистограмма накопительной доходности в Excel
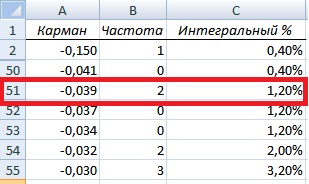
Итак первый столбец полученной таблицы это квантиль данного для распределения доходностей/убытков, вторая частота попадания доходностей в тот или иной интервал, третья отражает вероятность появления убытков. В таблице с накопительной вероятностью попадания в тот или иной интервал необходимо найти уровень
Определение квантиля доходностей акции «ручным способом»
Результат оценки «ручным способом» меры риска VaR в Excel
Сложность использования метода оценки риска VaR
Отечественный фондовый рынок имеет достаточно высокую степень волатильности, на рынке наблюдаются «тяжелые хвосты» – то есть возникновение частых кризисов с большим размером убытков. В результате модель VaR не может точно спрогнозировать возможные будущие потери инвестора. Следует отметить, что данная модель хорошо применима для товарных низковолательных рынков нежели фондовых.
 | ★ Программа InvestRatio — расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса |
Резюме
В данной статье мы рассмотрели методы оценки риска на примере акции ОАО «Газпром», для этого пошагово разобрали, как строится современная оценка риска Value at Risk (VaR) в Excel двумя способами: дельта нормальным моделированием и «ручным способом».
Автор: к.э.н. Жданов Иван Юрьевич