Что такое std в статистике
Среднеквадратическое (стандартное) отклонение
Определение
Среднеквадратическое отклонение (англ. Standard Deviation, SD) является показателем, который используется в теории вероятности и математической статистике для оценки степени рассеивания случайной величины относительно ее математического ожидания. В инвестировании стандартное отклонение доходности ценных бумаг или портфеля используется для оценки меры риска. Чем выше степень рассеивания доходности ценной бумаги относительно ожидаемого доходности (математическое ожидание доходности), тем выше риск инвестирования, и наоборот.
Среднеквадратическое отклонение как правило обозначается греческой буквой σ (сигма), а стандартное отклонение латинской буквой S или как Std(X), где X – случайная величина.
Формула
Истинное значение среднеквадратического отклонения
Если известно точное распределение дискретной случайной величины, а именно, известно ее значение при каждом исходе и может быть оценена вероятность каждого исхода, то формула расчета среднеквадратического отклонения будет выглядеть следующим образом.
Где Xi – значение случайной величины X при i-ом исходе; M(X) математическое ожидание случайной величины X; pi – вероятность i-го исхода; N – количество возможных исходов.
При этом математическое ожидание случайной величины рассчитывается по формуле:
Стандартное отклонение генеральной совокупности
На практике вместо точного распределение случайной величины обычно доступна только выборка данных. В этом случае рассчитывается оценочное значение среднеквадратического отклонения, которое в этом случае называют стандартным отклонением (S). Если оценка основывается на всей генеральной совокупности данных, необходимо использовать следующую формулу.
Где Xi – i-ое значение случайной величины X; X – среднеарифметическое генеральной совокупности; N – объем генеральной совокупности.
Стандартное отклонение выборки
Если используется не вся генеральная совокупность данных, а выборка из нее, то формула расчета стандартного отклонения основывается на несмещенной оценке дисперсии.
Где Xi – i-ое значение случайной величины X; X – среднеарифметическое выборки; N – объем выборки.
Примеры расчета
Пример 1
Портфельный менеджер должен оценить риски инвестирования в акции двух компаний А и Б. При этом он рассматривает 5 сценариев развития событий, информация по которым представлена в таблице.
Поскольку нам известно точное распределение доходности каждой из акций, мы можем рассчитать истинное значение среднеквадратического отклонения доходности для каждой из них.
Шаг 1. Рассчитаем математическое ожидание доходности для каждой из акций.
Шаг 2. Подставим полученные данные в первую формулу.
Как мы можем видеть, акции Компании А характеризуются меньшим уровнем риска, поскольку у них ниже среднеквадратическое отклонение доходности. Следует также отметить, что и ожидаемая доходность у них ниже, чем у акций Компании Б.
Пример 2
Аналитик располагает данными о доходности двух ценных бумаг за последние 5 лет, которые представлены в таблице.
Поскольку точное распределение доходности неизвестно, а в распоряжении аналитика есть только выборка из генеральной совокупности данных, мы можем рассчитать стандартное отклонение выборки на основании несмещенной дисперсии.
Шаг 1. Рассчитаем ожидаемую доходность для каждой ценной бумаги как среднеарифметическое выборки.
X А = (7 + 15 + 2 – 5 + 6) ÷ 5 = 5%
X Б = (3 – 2 + 12 + 4 +8) ÷ 5 = 5%
Шаг 2. Рассчитаем стандартное отклонение доходности для каждой из ценных бумаг по формуле для выборки из генеральной совокупности данных.
Следует отметить, что обе ценные бумаги имеют равную ожидаемую доходность 5%. При этом стандартное отклонение доходности у ценной бумаги Б ниже, что при прочих равных делает ее более привлекательным объектом инвестирования в следствие лучшего профиля риск-доходность.
Стандартное отклонение в Excel
В Excel предусмотрено две функции для расчета стандартного отклонения выборки и генеральной совокупности.
Для выборки воспользуйтесь функцией «СТАНДОТКЛОН.В»:
Для генеральной совокупности используется функция «СТАНДОТКЛОН.Г»:
Интерпретация
В инвестировании стандартное отклонение доходности используется в качестве меры волатильности. Чем выше его значение, тем выше риск, связанный с инвестированием в этот актив, и наоборот. При прочих равных параметрах, предпочтение следует отдавать тому активу, у которого этот показатель будет минимальным.
Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Расчет дисперсии в Excel
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Стандартное отклонение
Стандартное отклонение — классический индикатор изменчивости из описательной статистики.
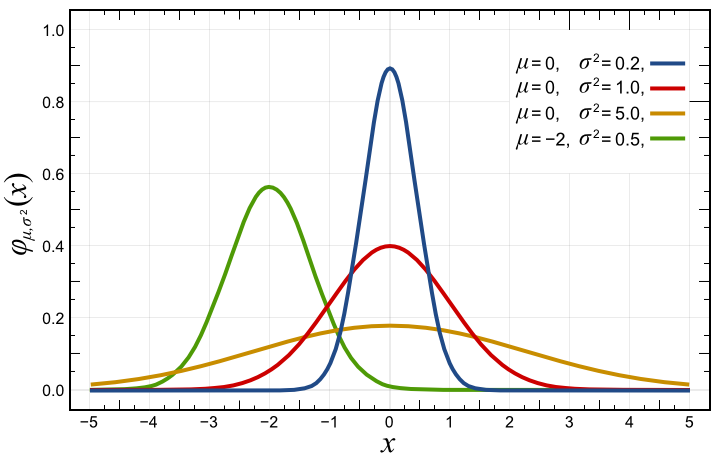
Стандартное отклонение, среднеквадратичное отклонение, СКО, выборочное стандартное отклонение (англ. standard deviation, STD, STDev) — очень распространенный показатель рассеяния в описательной статистике. Но, т.к. технический анализ сродни статистике, данный показатель можно (и нужно) использовать в техническом анализе для обнаружения степени рассеяния цены анализируемого инструмента во времени. Обозначается греческим символом Сигма «σ».
Спасибо Карлам Гауссу и Пирсону за то, что мы имеем возможность пользоваться стандартным отклонением.
Используя стандартное отклонение в техническом анализе, мы превращаем этот «показатель рассеяния» в «индикатор волатильности«, сохраняя смысл, но меняя термины.
Что представляет собой стандартное отклонение
Понимание сути стандартного отклонения возможно с пониманием азов описательной статистики. К примеру, мы имеем 2 выборки, у которых среднее арифметическое одинаково и равно 3. Казалось бы, одинаковое среднее делает эти две выборки одинаковыми. Ан-нет! Давайте рассмотрим возможные варианты данных для этих двух выборок:
Очевидно, что разброс (или рассеяние, или, в нашем случае, волатильность) гораздо больше во второй выборке. Следовательно, несмотря на то, что у этих двух выборок одинаковое среднее (равное 3), они совершенно разные в силу того, что у второй выборки данные беспорядочно и сильно рассеяны вокруг центра, а у первой — сконцентрированы около центра и упорядочены.
Но если нам надо быстро дать понять о таком явлении, мы не будем объяснять, как в абзаце выше, а просто скажем, что у второй выборки очень большое стандартное отклонение, а у первой — очень маленькое. Так, у второй выборки стандартное отклонение равно 186, а у первой оно равно 1,6. Разница существенная.
Стандартное отклонение в техническом анализе
Стандартное отклонение используется в техническом анализе не так часто, но оно служит отличным индикатором волатильности (изменчивости). Стандартное отклонение используется для промежуточных вычислений различных индикаторов, таких как, например, Полосы Боллинджера или Ширина Полос Боллинджера.
Но помимо промежуточных вспомогательных вычислений, стандартное отклонение вполне приемлемо для самостоятельного вычисления и применения в техническом анализе. Как отметил активный читатель нашего журнала burdock, «до сих пор не пойму, почему СКО не входит в набор стандартных индикаторов отечественных диллинговых центров«.
Действительно, стандартное отклонение может классическим и «чистым» способом измерить изменчивость инструмента. Но к сожалению, этот индикатор не так распространен в анализе ценных бумаг.
Применение стандартного отклонения
Для любого индикатора нам понадобится переменная, т.е. параметр. В данном случае нам нужен только период n, который указывает, какое количество периодов мы будем включать в вычисление стандартного отклонения.
Для вычисления, мы берем данные закрытия из n периодов назад от последней доступной цены. Т.е. если мы установили период индикатора 20 (достаточно часто используемый период),то мы берем 20 последних данных и оперируем ими для вычисления стандартного отклонения сегодня. Следовательно, для вычисления стандартного отклонения в любой момент времени k, надо взять цены закрытия всех n периодов назад от k.
Вычисление стандартного отклонения
Предупреждаю, что самостоятельное вычисление вам врядли понадобиться, т.к. основные программы обработки данных имеют встроенную функцию вычисления стандартного отклонения. Например, в Microsoft Excel эта функция называется СТАНДОТКЛОН.
Вручную вычислить стандартное отклонение не очень интересно, но полезно для опыта. Стандартное отклонение можно выразить формулой STD=√[(∑(x- x ) 2 )/n], что звучит как корень из суммы квадратов разниц между элементами выборки и средним, деленной на количество элементов в выборке.
Если количество элементов в выборке превышает 30, то знаменатель дроби под корнем принимает значение n-1. Иначе используется n.
Пошагово вычисление стандартного отклонения:
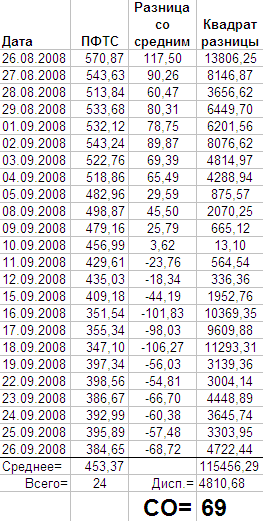
Для наглядности, вот пример из таблицы Excel:
В данном примере я взял краткий отрезок исторических данных цен закрытия индекса ПФТС. Для вычислений, дата не нужна, но я решил ее оставить, чтоб вы могли сверить, если хотите. Что действительно важно, это все остальное. Обратите внимание на отдельные данные под темным разделителем: «среднее» и «всего». Есть столбец с ценой закрытия, столбец с разницами данных и среднего, и квадраты этих разниц.
После вычисления квадратов, мы складываем их, полученную сумму делим на количество элементов выборки (т.к. всего элементов 24, что меньше 30) и из полученного честного вычисляем квадратный корень. Результат округляем до целого, и получаем 69.
Важно заметить, что все эти вычисления дадут нам лишь значение индикатора «стандартное отклонение» в последний день, т.е. 26.09.2008, а для каждой другой даты надо проделывать этот комплекс операций отдельно.
Прикладное значение стандартного отклонения
Напомню, что смысл стандартного отклонения заключается в выявлении степени изменчивости инструмента. Т.е. стандартное отклонение не сможет показать аналитику ничего, кроме волатильности.
Важно отметить, что элементы выборки в среднем отличается от среднего значения на ±СО. Т.е. из примера выше, цены закрытия индекса ПФТС в среднем отличаются от среднего значения на ±69.
Из примера выше, отдельно цифра 69 ничего не скажет, т.к надо ее использовать с другими значениями стандартного отклонения в другие периоды. 69 — относительно немалая волатильность, но если в другие периоды стандартное отклонение будет больше 100, то, естественно, 69 окажется умеренной изменчивостью. Т.е. «все познается в сравнении«.
Вывод
Стандартное отклонение — классический индикатор изменчивости из описательной статистики. Он поможет увидеть, как изменяется волатильность инструмента во времени.
Читайте также
комментария 23
Я уже 4 дня по формулам в интрнете пытаюсь рассчитать СО и вообще понять ЧЕ ЭТО ТАКОЕ.
Вы себе не представляете каким счастливым вы меня сделали!
Статья очень доходчиво написана. Тут и пример есть и программа в Экселе и минимум текста, но за-то каждое слово ценно. СПАСИБО.
Да!! Согласен с Читателем!Статья действительно отличная, как и все остальные на этом сайте!
Спасибо!
В разделе «Вычисление стандартного отклонения» есть такая формулировка:
«Стандартное отклонение можно выразить формулой STD=√[(∑(x-x)2)/n], что звучит как корень из суммы разниц между элементами выборки и средним, деленной на количество элементов в выборке».
Следует читать:
«Стандартное отклонение можно выразить формулой STD=√[(∑(x-x)2)/n], что звучит как корень из суммы квадратов разниц между элементами выборки и средним, деленной на количество элементов в выборке».
Если оценивать материал в целом, то подан он очень добротно (доходчиво).
Вам не кажется, что тут закралась некоторая ошибка?
если для выборки 1,2,3,4,5 брать знаменатель n (=5), то среднеквадратичное отклонение будет 1.5, а не 1.6 как пишется в статье.
По другим источникам, получается наоборот — при малом количестве выборок берется n-1, при большом берется любое — либо n, либо n-1.
Более того этим и отличаются «стандартное отклонение» (n-1) от «среднеквадратичного» (n)
Друзья,спасибо Вам огромное,ВЫ оч оч оч оч оч помогли,я как начинающий пытался долго понять,что это такое и зачем нужно,но в учебниках все одна вода,спасибо за ясность,которую вы внесли в подобного рода коллапс=)
Респект=)
Статья понравилась, иногда даже слишком подробная.
Но вкралась ошибочка:
«Важно отметить, что элементы выборки в среднем отличается от среднего значения на ±СО»
Элементы выборки отличаются в среднем на sum(abs(отклонений от среднего))/n (В excel — СРОТКЛ()), а Стандартное отклонение, как показал мой скромный опыт (могу ошибаться) — более отзывчивый к изменчивости/волатильности индикатор.
n берется если вы вычисляете СКО для генеральной совокупности, если вы имеете дело с выборкой, то берется n-1. А СКО и СО ничем, кроме названия друг от друга не отличаются..
Надо отдать должное автору, статья замечательная, лучшая из всех, с которыми мне приходилось знакомиться, понятная даже школьникам. После таких статей начитаешь любить математику и статистику. На мой взгляд, статья будет полнее, если привести простые и яркие примерами, где это можно применить.
Согласен с Сомневающимся в части 1,5 а не 1,6. Если отбросить данные извне формулы СО и дисперсии, а рассуждать с точки зрения простой логики. Тогда среднее отклонение от среднеарифметического вычисляется как среднеарифметическое модулей разностей отклонений от среднеарифметического, т.е. (мод(3-2)+мод(3-1)+мод(3-4)+ мод(3-5))/4 = 1,5. Что и понятно логически — лежит ровно посередине между 4 и 5 или 1 и 2. И в этом есть геометрический смысл. А по формулам выходит 1,6. Понять не могу. Может, кто-нить просветит?
Отличная статья. Спасибо автору.
А что касается n, то, похоже, действительно неточность. Т.к. при больших n вычитание единицы будет оказывать весьма незначительное воздействие на результат и им можно пренебречь. Т.о. при малых n следует использовать n-1, а при больших — единицу можно не вычитать.
Это просто потрясающая статья. Я по-моему весь интернет перелопатила, чтобы хоть что-нибудь понять.
Огромное спасибо автору.
Было бы по больше нормальных, коротких и понятных статей)))
спасибо Вам, Человек. огромный респектище, даже мне-имбецилу стало понятно. и пох, что мой коммент Вам не всрался, пардон за мой французский
….присоединяюсь к благодарностям, только что очень выручил. Только с этого сайта скатала объяснения нормальные.
Статья прекрасная! Долго не могла найти такого доходчивого и понятного описания. То, что нужно! Спасибо большое автору!
Нормально! Я все поняла!
Спасибо.
Очень доходчивая статья, прочитал на одном дыхании) Все просто и ясно изложена, согласен с Игорем, после прочтения статьи начинаешь больше интересоваться статистикой. Добавляю сайт в закладки. Спасибо!
Мне не совсем понятно утверждение: «элементы выборки в среднем отличается от среднего значения на ±СО.» Насколько я помню, значение искомой величины есть [x]± t*CO/(корень из n), где t-коэф.Стьюдента, n — количество элементов.
например применяется в xyz анализе, для определения классов товаров и для определения по ним страхового запаса ввиде прибавления СКО к среднему значению в условиях неопределенности
спасибо, очень доступное раскрытие сложного математического термина, если это возможно — посмотрите на стандартное отклонение в программе Wealth-Lab Developer 3.01. Написал алгоритм, хочу заавтоматить, но не могу нормальное ТЗ для программиста составить, споткнулся на формуле STDDEV, заранее благодарен.
По приведенной формуле нерационально рассчитывать СО, поскольку она требует два прохода (расчет среднего и дисперсии)формулу можно изменить и считать за один проход (сумму и сумму квадратов). Формулу не привожу, боюсь налажал с n. Надо в Нете поискать.
Отличная статья, но осталось непонятным, как рассчитывается канал Стандарное отклонение в терминале Метатрейдер 4
Спасибо автору статьи. Дело в том что я преподаю Excel для продвинутых пользователей и как раз собирался дат лекцию по стандартному отклонению. Так как моя специальность не статистик нуждался в таком доходчивом объяснении для для таких чайников как я. Отзыв оставляю для того чтобы автор продолжал писать такие статьи.
Привет из Баку!
Глубокоуважаемый автор, спасибо за замечательную статью, но, может быть я ошибаюсь, но в вашем алгоритме пошагового вычисления закралась ошибка.
Пошагово вычисление стандартного отклонения сначала нужно суммировать значения, затем возводить в квадрат, т.к. квадрат даже отрицательного числа будет положительным. В этом случае дисперсное значение будет неверным. Жду ответа.