Что такое solve в математике
Документация
Решите уравнения и неравенства
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Синтаксис
Описание
solve функция обеспечивает объединенный интерфейс ко множеству специализированных решателей. Смотрите Выбор Решателя.
Если вы не задаете indeterminates, для которого вы хотите решить уравнение, неравенство или систему, решатель использует набор всего indeterminates. Indeterminates должен быть идентификаторами или индексированными идентификаторами. Вы не можете использовать математические константы, такие как PI, ЭЙЛЕР, и так далее, как indeterminates. Решатель отбрасывает indeterminates, которые появляются только в именах функций или индексах. Смотрите Пример 12.
Если вы задаете список indeterminates, для которого вы хотите решить уравнение, неравенство или систему, решатель сортирует компоненты получившихся векторов решения согласно порядку indeterminates, который вы использовали. Если вы задаете indeterminates как набор, MuPAD ® может изменить порядок indeterminates.
Решатель может возвратить следующие типы наборов:
Конечные множества (вводят DOM_SET ).
Нулевые наборы полиномов (вводят RootOf ). Решатель возвращает набор этого типа, если это не может решить уравнение явным образом в терминах радикалов. Решатель также может возвратить этот тип набора, когда вы используете MaxDegree опция.
Отобразите наборы функций (введите Dom::ImageSet ).
Кусочные объекты, в которых каждая ветвь задает набор одного из допустимых типов (вводят piecewise ).
Для систем решатель возвращает набор векторов или набор списков уравнений. Чтобы указать, что решатель должен возвратить набор векторов, используйте VectorFormat опция. Смотрите Пример 10.
Неравенство a или a содержит только, когда обе стороны представляют вещественные числа. В частности, a = b не подразумевает тот a для комплексных чисел.
solve функция является символьным решателем. Если вы хотите использовать числовые методы, смотрите numeric::solve страница справки для доступных параметров и примеров.
Если числитель содержит учтенный полином с кратностью, больше, чем 1, решатель не проверяет, что несколько поддерживают нули в знаменателе. Смотрите Пример 17.
Взаимодействия среды
solve реагирует на свойства идентификаторов.
Примеры
Пример 1
Решите следующее уравнение. Как правило, для уравнений с конечным числом решений, решатель возвращает набор DOM_SET ввод:
Документация
Уравнения и системный решатель
Синтаксис
Описание
Примеры
Решите квадратное уравнение
Решите квадратное уравнение, не задавая переменную, чтобы решить для. solve выбирает x возвратить решение.
Решите полином и возвратите действительные решения
Решите полином пятой степени. Это имеет пять решений.
Численно решите уравнения
Попытайтесь решить следующее уравнение. solve возвращает числовое решение, потому что оно не может найти символьное решение.
Постройте левые и правые стороны уравнения. Заметьте, что уравнение также имеет положительное решение.
Найдите другое решение путем прямого вызова числового решателя vpasolve и определение интервала.
Решите многомерные уравнения и присвойте Выходные параметры структуре
При решении для нескольких переменных может быть более удобно сохранить выходные параметры в массиве структур, чем в отдельных переменных. solve функция возвращает структуру, когда вы задаете один выходной аргумент, и существуют несколько выходных параметров.
Решите систему уравнений, чтобы возвратить решения в массиве структур.
Доступ к решениям путем обращения к элементам структуры.
Используя массив структур позволяет вам удобно заменять решениями в другие выражения.
Используйте subs функционируйте, чтобы заменить решениями S в другие выражения.
Если solve возвращает пустой объект, затем никакие решения не существуют.
Решите неравенства
solve функция может решить неравенства и возвратить решения, которые удовлетворяют неравенствам. Решите следующие неравенства.
Установите ‘ReturnConditions’ к true возвратить любые параметры в решении и условиях на решении.
Решите многомерные уравнения и присвойте Выходные параметры переменным
Решите систему уравнений.
При решении больше чем для одной переменной порядок, в котором вы задаете переменные, задает порядок, в котором решатель возвращает решения. Присвойте решения переменных solv и solu путем определения переменных явным образом. Решатель возвращает массив решений для каждой переменной.
Записи с тем же индексом формируют пару решений.
Используйте параметры и условия совершенствовать решение
Сократите результат с правилами упрощения
Установите ‘IgnoreAnalyticConstraints’ к true применять правила упрощения, которые могут позволить solve найти решение. Для получения дополнительной информации см. Алгоритмы.
solve применяет упрощения, которые позволяют решателю находить решение. Математические правила применялись, когда выполняющие упрощения не всегда допустимы в целом. В этом примере решатель применяет логарифмические тождества учитывая, что x положительное вещественное число. Поэтому решения, найденные в этом режиме, должны быть проверены.
Проигнорируйте предположения на переменных
sym и syms функции позволяют вам установить предположения для символьных переменных.
Примите что переменная x положительно.
Решите полиномиальные знатные уравнения
Когда вы решаете полиномиальное уравнение, решатель может использовать root возвратить решения. Решите полином третьей степени.
Возвратите одно решение
Вместо того, чтобы возвратить бесконечное множество периодических решений, решатель выбирает три решения, что он считает самым практическим.
Входные параметры
eqn — Уравнение, чтобы решить
символьное выражение | символьное уравнение
var — Переменная, для которой вы решаете уравнение
символьная переменная
eqns Система уравнений
символьные выражения | символьные уравнения
vars — Переменные, для которых вы решаете уравнение или систему уравнений
символьный вектор | символьная матрица
Порядок, в котором вы задаете эти переменные, задает порядок, в котором решатель возвращает решения.
Аргументы name-value
Real — Отметьте для возврата только действительных решений
false (значение по умолчанию) | true
Отметьте для возврата только действительных решений в виде разделенной запятой пары, состоящей из ‘Real’ и одно из этих значений.
| false | Возвратите все решения. |
| true | Возвратите только те решения, для которых каждое подвыражение исходного уравнения представляет вещественное число. Эта опция также принимает, что все символьные параметры уравнения представляют вещественные числа. |
ReturnConditions — Отметьте для возврата параметров и условий
false (значение по умолчанию) | true
Отметьте для возврата параметров в решении и условиях, при которых решение верно в виде разделенной запятой пары, состоящей из ‘ReturnConditions’ и одно из этих значений.
IgnoreAnalyticConstraints — Правила упрощения применились к выражениям и уравнениям
false (значение по умолчанию) | true
Правила упрощения применились к выражениям и уравнениям в виде разделенной запятой пары, состоящей из ‘IgnoreAnalyticConstraints’ и одно из этих значений.
| false | Используйте строгие правила упрощения. |
| true | Примените чисто алгебраические упрощения в выражениях и уравнениях. Установка IgnoreAnalyticConstraints к true может дать вам простые решения, которые могли привести к результатам, не обычно допустимым. Другими словами, эта опция применяет математические тождества, которые удобны, но результаты не могут содержать для всех возможных значений переменных. В некоторых случаях это также включает solve решить уравнения и системы, которые не могут быть решены в противном случае. |
IgnoreProperties — Отметьте для возврата решений, противоречивых со свойствами переменных
false (значение по умолчанию) | true
Отметьте для возврата решений, противоречивых со свойствами переменных в виде разделенной запятой пары, состоящей из ‘IgnoreProperties’ и одно из этих значений.
| false | Не включайте решения, противоречивые со свойствами переменных. |
| true | Включайте решения, противоречивые со свойствами переменных. |
MaxDegree — Максимальная степень полиномиальных уравнений, для которых решатель использует явные формулы
2 (значение по умолчанию) | положительное целое число, меньшее, чем 5
Максимальная степень полиномиальных уравнений, для которых решатель использует явные формулы в виде положительного целого числа, меньшего, чем 5. Решатель не использует явные формулы, которые вовлекают радикалов при решении полиномиальных уравнений степени, больше, чем заданное значение.
PrincipalValue — Отметьте для возврата одного решения
false (значение по умолчанию) | true
Отметьте для возврата одного решения в виде разделенной запятой пары, состоящей из ‘PrincipalValue’ и одно из этих значений.
| false | Возвратите все решения. |
| true | Возвратите только одно решение. Если уравнение или система уравнений не имеют решения, решатель возвращает пустой символьный объект. |
Выходные аргументы
S — Решения уравнения
символьный массив
Решения уравнения, возвращенного как символьный массив. Размер символьного массива соответствует количеству решений.
Y — Решения системы уравнений
структура
y1. yN — Решения системы уравнений
символьные переменные
parameters — Параметры в решении
вектор из сгенерированных параметров
conditions — Условия, при которых решения допустимы
вектор из символьных выражений
Советы
Если параметр не появляется ни в каком условии, это означает, что параметр может взять любое комплексное число.
Чтобы решить дифференциальные уравнения, используйте dsolve функция.
При решении системы уравнений всегда присваивайте результат выходным аргументам. Выходные аргументы позволяют вам получить доступ к значениям решений системы.
MaxDegree только принимает положительные целые числа, меньшие, чем 5 потому что, в целом, нет никаких явных выражений для корней полиномов степеней выше, чем 4.
Алгоритмы
регистрируйте ( a) + журнал ( b) = журнал ( a · b) для всех значений a и b. В частности, следующее равенство допустимо для всех значений a, b и c:
журнал ( a b ) = b · регистрируйте ( a) для всех значений a и b. В частности, следующее равенство допустимо для всех значений a, b и c:
Решения полиномиальных уравнений должны быть завершены.
solve
Equations and systems solver
Syntax
Description
Examples
Solve Quadratic Equation
Solve the quadratic equation without specifying a variable to solve for. solve chooses x to return the solution.
Solve Polynomial and Return Real Solutions
Solve a fifth-degree polynomial. It has five solutions.
Numerically Solve Equations
Try solving the following equation. solve returns a numeric solution because it cannot find a symbolic solution.
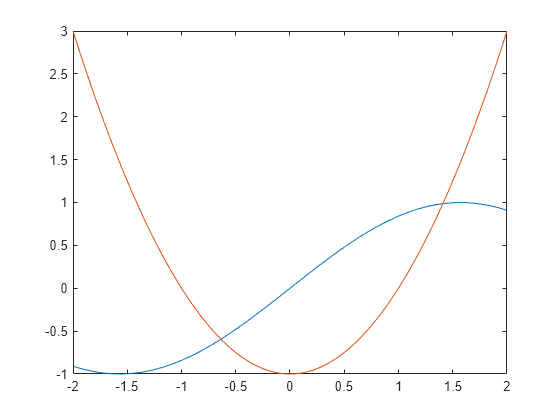
Plot the left and the right sides of the equation. Observe that the equation also has a positive solution.
Find the other solution by directly calling the numeric solver vpasolve and specifying the interval.
Solve Multivariate Equations and Assign Outputs to Structure
When solving for multiple variables, it can be more convenient to store the outputs in a structure array than in separate variables. The solve function returns a structure when you specify a single output argument and multiple outputs exist.
Solve a system of equations to return the solutions in a structure array.
Access the solutions by addressing the elements of the structure.
Using a structure array allows you to conveniently substitute solutions into other expressions.
Use the subs function to substitute the solutions S into other expressions.
If solve returns an empty object, then no solutions exist.
Solve Inequalities
The solve function can solve inequalities and return solutions that satisfy the inequalities. Solve the following inequalities.
Set ‘ReturnConditions’ to true to return any parameters in the solution and conditions on the solution.
Solve Multivariate Equations and Assign Outputs to Variables
Solve the system of equations.
When solving for more than one variable, the order in which you specify the variables defines the order in which the solver returns the solutions. Assign the solutions to variables solv and solu by specifying the variables explicitly. The solver returns an array of solutions for each variable.
Entries with the same index form the pair of solutions.
Use Parameters and Conditions to Refine Solution
Shorten Result with Simplification Rules
Set ‘IgnoreAnalyticConstraints’ to true to apply simplification rules that might allow solve to find a solution. For details, see Algorithms.
solve applies simplifications that allow the solver to find a solution. The mathematical rules applied when performing simplifications are not always valid in general. In this example, the solver applies logarithmic identities with the assumption that x is a positive real number. Therefore, the solutions found in this mode should be verified.
Ignore Assumptions on Variables
The sym and syms functions let you set assumptions for symbolic variables.
Assume that the variable x is positive.
Solve Polynomial Equations of High Degree
When you solve a polynomial equation, the solver might use root to return the solutions. Solve a third-degree polynomial.
Return One Solution
Instead of returning an infinite set of periodic solutions, the solver picks three solutions that it considers to be the most practical.
Input Arguments
eqn — Equation to solve
symbolic expression | symbolic equation
var — Variable for which you solve equation
symbolic variable
eqns — System of equations
symbolic expressions | symbolic equations
vars — Variables for which you solve an equation or system of equations
symbolic vector | symbolic matrix
The order in which you specify these variables defines the order in which the solver returns the solutions.
Name-Value Arguments
Real — Flag for returning only real solutions
false (default) | true
Flag for returning only real solutions, specified as the comma-separated pair consisting of ‘Real’ and one of these values.
| false | Return all solutions. |
| true | Return only those solutions for which every subexpression of the original equation represents a real number. This option also assumes that all symbolic parameters of an equation represent real numbers. |
ReturnConditions — Flag for returning parameters and conditions
false (default) | true
Flag for returning parameters in solution and conditions under which the solution is true, specified as the comma-separated pair consisting of ‘ReturnConditions’ and one of these values.
IgnoreAnalyticConstraints — Simplification rules applied to expressions and equations
false (default) | true
Simplification rules applied to expressions and equations, specified as the comma-separated pair consisting of ‘IgnoreAnalyticConstraints’ and one of these values.
| false | Use strict simplification rules. |
| true | Apply purely algebraic simplifications to expressions and equations. Setting IgnoreAnalyticConstraints to true can give you simpler solutions, which could lead to results not generally valid. In other words, this option applies mathematical identities that are convenient, but the results might not hold for all possible values of the variables. In some cases, it also enables solve to solve equations and systems that cannot be solved otherwise. |
IgnoreProperties — Flag for returning solutions inconsistent with properties of variables
false (default) | true
Flag for returning solutions inconsistent with the properties of variables, specified as the comma-separated pair consisting of ‘IgnoreProperties’ and one of these values.
| false | Do not include solutions inconsistent with the properties of variables. |
| true | Include solutions inconsistent with the properties of variables. |
MaxDegree — Maximum degree of polynomial equations for which solver uses explicit formulas
2 (default) | positive integer smaller than 5
Maximum degree of polynomial equations for which solver uses explicit formulas, specified as a positive integer smaller than 5. The solver does not use explicit formulas that involve radicals when solving polynomial equations of a degree larger than the specified value.
PrincipalValue — Flag for returning one solution
false (default) | true
Flag for returning one solution, specified as the comma-separated pair consisting of ‘PrincipalValue’ and one of these values.
| false | Return all solutions. |
| true | Return only one solution. If an equation or a system of equations does not have a solution, the solver returns an empty symbolic object. |
Output Arguments
S — Solutions of equation
symbolic array
Solutions of an equation, returned as a symbolic array. The size of a symbolic array corresponds to the number of the solutions.
Y — Solutions of system of equations
structure
y1. yN — Solutions of system of equations
symbolic variables
parameters — Parameters in solution
vector of generated parameters
conditions — Conditions under which solutions are valid
vector of symbolic expressions
If a parameter does not appear in any condition, it means the parameter can take any complex value.
To solve differential equations, use the dsolve function.
When solving a system of equations, always assign the result to output arguments. Output arguments let you access the values of the solutions of a system.
MaxDegree only accepts positive integers smaller than 5 because, in general, there are no explicit expressions for the roots of polynomials of degrees higher than 4.
Algorithms
log( a) + log( b) = log( a· b) for all values of a and b. In particular, the following equality is valid for all values of a, b, and c:
log( a b ) = b·log( a) for all values of a and b. In particular, the following equality is valid for all values of a, b, and c:
If f and g are standard mathematical functions and f( g( x)) = x for all small positive numbers, f( g( x)) = x is assumed to be valid for all complex values x. In particular:
W k( x· e x ) = x for all branch indices k of the Lambert W function.
The solutions of polynomial equations must be complete.
Решатели. или. Великолепная семерка Mathcad
Решатели
или
Великолепная семерка Mathcad
Многие задачи по физике, химии и другим школьным и вузовским дисциплинам сводятся к решению уравнения и систем уравнений. Поэтому полезно будет узнать, какие инструменты для решения такого рода задач есть у пакета Mathcad, очень популярного у школьников, студентов инженеров и ученых. Эти инструменты объединены в группу «Решение уравнений» встроенных функций Mathcad, которые используют различные численные методы. В этой группе традиционно находится семь функций. Есть еще в среде Mathcad, и оператор solve для символьного (аналитического) решения задач. Описание этих инструментов будет сделано на несложных школьных «водных» примерах.
Задача 1. Моторная лодка прошла по реке в одну сторону (L = 10 км), а потом вернулась в исходную точку, затратив на всю поездку 1 час 45 минут (t). Спрашивается, какова скорость течения воды в реке (неизвестная х), если собственная скорость лодки (v–скорость в стоячей воде) равна 12 км/ч.
Раньше подобные «школьные» задачи решались в несколько действий[1]. Сейчас принято составлять, а затем решать алгебраическое уравнение, выбирая его подходящие корни. Пойдем по этому пути и мы, но, составив уравнение, попробуем решить его на компьютере. В нашей задаче о моторной лодке время в пути t – это суммарное время, затраченное на поездку в одну сторону (по течению реки) L / (v + x), и в обратную сторону (против течения реки) L / (v – x). Поэтому наше уравнение имеет вид:
(L / (v + x) ) + (L / (v – x) ) = t.
0. solve
Начнем с решения полученного уравнения средствами символьной математики. Формальное, более длинное название символьной математики – компьютерные аналитические преобразования, но у нас прижилась калька с английского – symbolic math. Ее, как принято, мы и будем использовать.
Если численная математика (которая, повторяем, тоже есть в среде Mathcad и составляет его основу) оперирует числами, хранящимися в переменных, то символьная – самими переменными-символами.
На рисунке 1 показано решение уравнения движения моторной лодки по реке с помощью команды solve символьной математики Mathcad[2].
Рис. 1.Аналитическое решение задачи о движении моторной лодки
Из полученного общего аналитического решения (из вектора с двумя элементами-формулами – см. рис. 1) можно скопировать один элемент, подставить в него исходные значения переменных L, t и v (см. рис. 2) и получить численный ответ – скорость течения воды в реке. Ответ будет выдан в метрах, деленных на секунду (Mathcad ориентирован на СИ), и подправлен на более привычные километры в час (kph).
Рис. 2. Решение задачи о моторной лодке по найденной на рис. 1 формуле
Спрашивается, для чего в пакете Mathcad есть численная математика, если задачу можно решить с помощью символьной? Дело в том, что символьная математика, нацеленная на выдачу всех решений в виде формул (абсолютная точность!), часто не справляется с более-менее сложной задачей, и это показано на рис. 3 и 4.
Рис. 3. Поиск корня уравнения: очень объемный ответ
На рис. 3 в уравнении движения моторной лодки один из иксов был возведен в квадрат. Физический смысл уравнения пропал (складывается скорость с квадратом скорости)[3], но сейчас не это важно. Важно то, что пакет Mathcad, решив это чуть усложненное уравнение, не смог показать нам ответ – настолько он стал громоздким. Но это еще полбеды, поскольку можно для получения ответа ввести конкретные числовые данные. Полная «беда» показана на рис. 4 для еще более сложного уравнения. Если, например, один икс возвести в квадрат, а другой в куб (рис. 4), то символьная математика Mathcad «поднимет руки вверх и скажет: «Сдаюсь!».
Рис. 4. Поиск корня уравнения: решение не найдено
Но если в символьные константы этого «нефизического» уравнения подставить безразмерные численные значения, то хотя бы один действительный корень у этого уравнения найти удастся – см. рис. 5, где данная задача решена графически.
Рис. 5. Графический поиск нуля функции
1. root + root
Из рис. 5 видно, что у нашего уравнения, превращенного в функцию пользователя переносом переменной t в левую часть, есть как минимум один действительный корень в районе 0.9. Уточнить численное значение этого корня поможет встроенная в Mathcad функция root – см. рис. 6 и 7.
Рис. 6. Работа в среде Mathcad встроенной функции root с четырьмя аргументами
На рис. 6 показан вызов функции root с четырьмя аргументами, а на рис. 7 с двумя. В первом случае нуль функции y(х) ищется методом деления пополам на интервале, заданном третьим и четвертым аргументами функции root (см. авторскую анимацию этого метода на сайте http://communities. /videos/1468). Во втором случае (рис. 7) нуль функции y(x) рассчитывается методом секущих с опорой на первое приближение х := 1 (http://communities. /videos/1466). В среде Mathcad для вычисления нуля функции пользователя фактически есть две одинаковые по имени, но разные по своей сути встроенные функции.
Рис. 7. Работа в среде Mathcad встроенной функции root с двумя аргументами
Ранее мы отметили, что символьная математика Mathcad оперирует не числами, а символами – самими переменными, хранящими или не хранящими числа. Но это не совсем так.
Если какая-либо переменная выражения хранит численное значение, то символьная математика будет работать не с самой переменной (с символом), а с числом, хранящимся в этой переменной. На рис. 3 была показана осечка символьной математики Mathcad при решении довольно простого уравнения. Но если переменным этого уравнения задать численные значения, то символьный оператор solve успешно справится с задачей – см. рис. 8.
Рис. 8. Численный ответ символьного оператора
На рис. 8 показано, что «символьный» оператор solve в отличие от «численной» функции root выдал все четыре корни уравнения: один действительный и три комплексных. К тому же, если численная математика при выводе ответа «на печать» по умолчанию ограничивается тремя знаками после запятой, то оператор solve в этом случае выдал численные решения с двадцатью знаками после запятой. При «численном» ответе количество значащих цифр можно увеличить до 15, а при символьном до 250.
Если наше уравнение и дальше усложнять, то на каком-то этапе оператор solve откажется работать. Функция же root по-прежнему будет выдавать корень, правда, лишь один из многих и с опорой на заданный интервал поиска (рис. 6) или на первое приближение (рис. 7). При этом задавать интервал поиска придется, исходя из уверенности, что корень на этом интервале имеется, а метод секущих при неправильном первом приближении вообще не даст нужного результата. Это такой своеобразный компромисс. Отсюда общее правило: поставленную задачу нужно стараться сначала решить аналитически в общем виде, не придавая переменным конкретных численных значений. Если же это не получается, то придется переходить к поиску частных решений численными методами.
Уравнение движения моторной лодки, показанное на рис. 1, легко преобразовывается в квадратное. Как это можно сделать в среде Mathcad, показано на рис. 9.
Рис. 9. Определение коэффициентов полинома
Оператор символьной математики simplify приводит левую часть исходного выражения к общему знаменателю, умножает обе части уравнения на полученный знаменатель и переносит все слагаемые в левую часть уравнения (рис. 9). Таким способом выделяется функция, которая приравнена к нулю. Оператор coeffs находит коэффициенты этой функции-полинома (в данном случае квадратного).
2. polyroots
Если выражение представляет собой полином, то найти все его нули можно, использовав еще одну функцию из «великолепной семерки Mathcad» – функцию polyroots, имеющую в качестве аргумента вектор коэффициентов полинома и возвращающую его нули (вектор, который на один элемент короче вектора-аргумента – см. рис. 10), т. е. решение нашей задачи.
Рис. 10. Поиск нулей полинома в среде Mathcad
В нашей задаче о движении моторной лодки полином оказался квадратным и его спокойно можно было решить через оператор символьной математики solve (см. рис. 1). Но в случае полиномов высокой степени оператор solve не сработает. Тут и пригодится численная встроенная функция polyroots.
3. Find
Показать работу еще одной функции из «великолепной семерки Mathcad» – функции Find – поможет нам еще одна дополнительная моторная лодка.
Задача 2. От двух пристаней на реке навстречу друг другу[4] одновременно отходят две моторные лодки. Они встречаются в точке, делящей этот участок реки в золотом соотношении[5]. Найти скорость второй лодки v2 и скорость течения воды в реке v, если известна скорость первой лодки v1, расстояние между пристанями L и время t движения лодок до момента встреча.
Золотое сечение в эту задачу вставлено неслучайно. Можно поискать в своей памяти или в справочниках (бумажных или интернетовских) формулу золотого сечения. Но можно поступить проще: в среде Mathcad написать само уравнение золотого сечения и решить его – см. рис. 11.
Рис. 11. Решение уравнения золотого сечения в среде Mathcad
На рисунке 12 показано решение в среде Mathcad Prime и Mathcad 15 задачи о двух моторных лодках, сводящееся к решению системы двух алгебраических уравнений с двумя неизвестными. Решение найдено с помощью функции Find.
Рис. 12. Решение систем алгебраических уравнений с помощью функции Find
Встроенная функция Find меняет значение своих аргументов, начиная от начального приближения так, чтобы уравнения системы превратились в тождества. Вернее, почти в тождества. Дело в том, что функции root (рис. 7 и 8) и Find (рис. 7) возвращают значения, отличающиеся от точных решений на величину, не превышающую по модулю значения, хранящегося в системной переменной CTOL. Ведь что такое корень уравнения?! Это такое значение неизвестного, при подстановке которого в уравнение мы получаем тождество. Но при численном (приближенном!) решении подстановка корня в уравнение приводит к тому, что правые и левые части уравнений хоть и не совпадают, но отличаются друг от друга на значение, хранимое в переменной CTOL, которое по умолчанию равно 0.001. Это значение можно менять, решая конкретную задачу.
4. lsolve
Можно понять, что система двух алгебраических уравнений движения двух моторных лодок навстречу друг другу линейна, и применить к ней еще одну функцию из «великолепной семерки Mathcad» – функцию lsolve, предназначенную для решения (solve) именно систем линейных (l) алгебраических уравнений (СЛАУ) – см. рис. 13.
Рис. 13. Решение СЛАУ в среде Mathcad
На рисунке 13 система уравнений, показанная на рис. 12, преобразована к виду классической системы: слева неизвестные с коэффициентами, справа свободные члены. Функция lsolve имеет два аргумента: матрицу коэффициентов при неизвестных СЛАУ (у нас это M) и вектор свободных членов V. Возвращает функция lsolve вектор найденных значений неизвестных.
5 и 6. Minimize & Maximize
Очередная функция «великолепной семерки» ─ функция Minimize, будет проиллюстрирована на примере одной задачи оптимизации, связанной также с «водным транспортом».
Задача 3. Определить крейсерскую скорость судна – скорость при которой затраты на его эксплуатацию будут минимальны.
Задача предельно упрощена – затраты на эксплуатацию судна состоят двух частей: почасовой зарплаты экипажа, пропорциональной времени движения судна (обратно-пропорциональной скорости судна), и затрат на горючее, пропорциональных квадрату скорости судна. Коэффициенты пропорциональности – а и b. Увеличивая скорость судна, мы меньше платим экипажу, но при этом приходится больше тратить денег на горючее.
На рисунке 14 показано решение этой типичной задачи оптимизации с помощью встроенной функции Minimize с графической иллюстрацией решения.
Рис. 14. Нахождение крейсерской скорости судна численной математической Mathcad
Функция Minimize меняет значение своего второго аргумента, начиная от заданного предполагаемого значения (у нас это 10 км/ч) так, чтобы значение первого аргумента (целевой функции Удельные_затраты) приняло минимальное значение. Если бы мы не минимизировали затраты, а максимизировали прибыль, например, то нужно было бы при решении задачи функцию Minimize заменить на функцию Maximize. В оптимизационных задачах часто присутствуют ограничения – скорость судна, например, не может превышать максимально допустимую. В этом случае функции Minimize и Maximize нужно будет поместить в область Ограничения блока Решить, показанного на рис. 12.
Найти минимум нашей целевой функции можно и средствами символьной математики Mathcad, что показано на рис. 15.
Рис. 15. Нахождение крейсерской скорости судна символьной математикой Mathcad
На рисунке 15 ведется поиск нулей первой производной целевой функции по удельным затратам на километр пути судна. Но если затраты на топливо будут зависеть от скорости судна, взятой не во второй степени, а в степени n, то символьная математика уже не справится с такой усложненной задачей (рис. 16), и придется вернуться к численным методам (рис. 14).
Рис. 16. Осечка при работе с символьной математикой Mathcad
7. Minerr
Последняя функция «великолепной семерки» Mathcad – это функция Minerr: Minimal Error – минимальная ошибка. Если функция Find (см. рис. 12) не находит решения системы уравнений, то она возвращает сообщение об ошибке. Функция же Minerr в такой ситуации возвратит не сообщение об ошибке, а значения своих аргументов (невязку системы), при которых система уравнений будет максимально приближена к системе тождеств – точку последнего приближения к решению. В старых версиях Mathcad не было функций Minimize и Maximize, и оптимизационные задачи приходилось решать через функцию Minerr. На рисунке 17 показано, как эта функция решает нашу задачу оптимизации скорости судна: при оптимальной скорости затраты на эксплуатацию судна будут максимально приближены к нулю.
Рис. 17. Решение задачи оптимизации с помощью функции Minerr
Функцию Minerr можно считать главной в «великолепной семерке Mathcad», т. к. ею можно заменить и функцию Find, и функцию root (в двух ее вариантах), и функцию polyroots, и функцию lsolve, и функцию Minimize, и функцию Maximize.
7+1. Odesolve
Итак, задача 4. На моторной лодке, движущейся со скоростью v, заглушили мотор. Спрашивается, как будут меняться скорость лодки и пройденный ею путь? Задача предельно упрощена – на лодку действует сила трения, пропорциональная квадрату скорости лодки (см. рис. 14, 15, 16 и 17, где этот квадрат фигурировал). На рисунке 18 показано решение и графическое отображение этой задачи с помощью функции Odesolve.
Рис. 18. Решение задачи об остановки лодки
Коэффициент пропорциональности, записанный в уравнении на рис. 18 (масса лодки, помноженная на ускорение – на первую производную скорости по времени), состоит из двух частей, связанных с трением о воздух надводной части лодки и трением о воду ее подводной части. Эти коэффициенты пропорциональны плотности ρ среды (воздуха или воды) и площади поперечного сечения надводной и подводной частей лодки S.
Задачу об остановке моторной лодки мы решили численно: функция Odesolve не ищет аналитического решения уравнения. Она формирует таблицу значений искомых функций v (скорость лодки) и x (пройденный путь), по которым интерполяцией создается непрерывная функция, по которой мы построили графики (см. рис. 18).
В среде Mathcad нет средств аналитического (символьного) решения дифференциальных уравнений. Но их можно поискать и найти в Интернете. На рисунке 19 показано такое решение – логарифмическая функция. Оно нашлось, поскольку исходное уравнение было достаточно простым. Но если с нашей задачи начать снимать ограничения, позволяющие упростить уравнение, то символьного решения уже не будет, и нам придется возвращаться к численным методам – к функции Odesolve. Так, например, при торможении лодки площадь поперечного сечения ее надводной части уменьшается, а подводной части растет[6]. Коэффициенты kвозд и kводы (см. блок исходных данных на рис. 18) также зависят от скорости и характера движения лодки: они одни при ламинарном («гладком») обтекании тела и другие при турбулентном движении, когда за лодкой клубятся вихри воды и воздуха. У воды и воздуха разная вязкость, что тоже нужно учитывать при математическом моделировании движении лодки. Этим занимается очень интересная наука под названием гидрогазодинамика…
Рис. 19. Символьное решение дифференциального уравнения
Выводы
Каждая из рассмотренных функций «великолепной семерки Mathcad» обладает своими особенностями и ограничениями. Прежде чем приступать к решению задачи, следует продумать, какая из опций Mathcad приведет к поставленной цели, причем наилучшим образом.
Школьнику, студенту, инженеру или ученому необходимо (а в ряде случаев и достаточно) освоить «великолепную семерку Mathcad», особенности численных, графических и аналитических методов решения задач, чтобы успешно решать на компьютере свои учебные или профессиональные задачи.
Литература:
Очков математики и математические пакеты // Открытое образование, №2, 2013. С. 23-34 (http://twt. mpei. ac. ru/ochkov/Mathcad-15/OchkovMath-pdf. pdf)
[1]Первое действие: как долго лодка была бы в пути, если б вода в реке была неподвижна – 2*10 км/12 км/ч = 1 час 40 минут; второе действие… Читатель, докончи это решение сам и сравни с теми, которые приведены ниже. Мы по действиям такие задачи решали когда-то в 5 классе школы. Но не всякая задача может быть решена по действиям. Поэтому и была придумана алгебра. Эту задачу тоже сходу нельзя решить пошагово. В древние времена, пока не было формулы корней квадратного уравнения, не всякое квадратное уравнение могли решить, причем решения были очень хитроумными.
[2] На этом и некоторых других рисунках будут показаны инструменты Mathcad Prime и Mathcad 15 для решения описываемых задач.
[3] А такими «нефизическими» формулами заполнены все учебники и задачники по математике. И это очень плохо. Хорошо тогда, когда за формулой скрывается какая-нибудь физическая реальность.
[4] Навстречу друг другу по одноколейной дороге одновременно вышли два поезда. И не столкнулись. Почему? Ответ: не судьба! 😉
[5] Мы имеем в виду знаменитое «Золотое сечение», т. е. такое деление отрезка на две неравные части, при котором длина отрезка так относится к длине большей части, как длина большей части относится к длине меньшей.
[6] Самые быстроходные суда те, у которых подводная часть минимальна: глиссирующие суда, суда на подводных крыльях или на воздушной подушке.