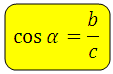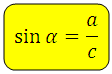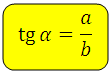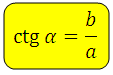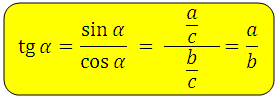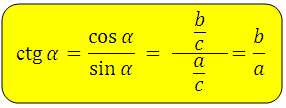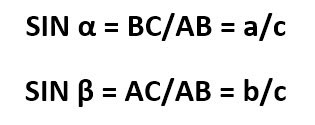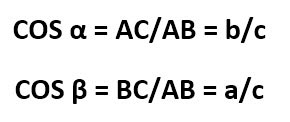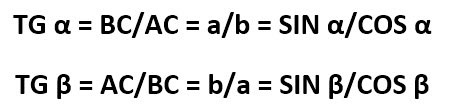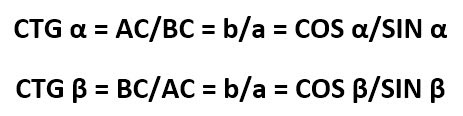Что такое sin в физике
Как определить косинус или синус в физике
Дело в том, что я не раз наблюдал, как учащиеся 10-11 классов с трудом вспоминают данные определения. Они прекрасно помнят, что катет относится к гипотенузе, а вот какой из них — забывают и путают. Цена ошибки, как вы знаете на экзамене – это потерянный бал.
Информация, которую я представлю непосредственно к математике не имеет никакого отношения. Она связана с образным мышлением, и с приёмами словесно-логической связи. Именно так, я сам, раз и на всегда запомнил данные определения. Если вы их всё же забудете, то при помощи представленных приёмов всегда легко вспомните.
Напомню определения синуса и косинуса в прямоугольном треугольнике:
Косинус острого угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе:
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Итак, какие ассоциации у вас вызывает слово косинус?
Наверное, у каждого свои 😉 Запоминайте связку:
Таким образом, у вас сразу в памяти возникнет выражение –
«… отношение ПРИЛЕЖАЩЕГО катета к гипотенузе ».
Проблема с определением косинуса решена.
Если нужно вспомнить определение синуса в прямоугольном треугольнике, то вспомнив определение косинуса, вы без труда установите, что синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе. Ведь катетов всего два, если прилежащий катет «занят» косинусом, то синусу остаётся только противолежащий.
Как быть с тангенсом и котангенсом? Путаница та же. Учащиеся знают, что это отношение катетов, но проблема вспомнить какой к которому относится – то ли противолежащий к прилежащему, то ли наоборот.
Тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему:
Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему:
Как запомнить? Есть два способа. Один так же использует словесно-логическую связь, другой – математический.
СПОСОБ МАТЕМАТИЧЕСКИЙ
Есть такое определение – тангенсом острого угла называется отношение синуса угла к его косинусу:
*Запомнив формулу, вы всегда сможете определить, что тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему.
Аналогично. Котангенсом острого угла называется отношение косинуса угла к его синусу:
Итак! Запомнив указанные формулы вы всегда сможете определить, что:
— тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему
— котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему.
СПОСОБ СЛОВЕСНО-ЛОГИЧЕСКИЙ
О тангенсе. Запомните связку:
То есть если потребуется вспомнить определение тангенса, при помощи данной логической связи, вы без труда вспомните, что это
«… отношение противолежащего катета к прилежащему»
Если речь зайдёт о котангенсе, то вспомнив определение тангенса вы без труда озвучите определение котангенса –
«… отношение прилежащего катета к противолежащему»
СПОСОБ УНИВЕРСАЛЬНЫЙ
Можно просто зазубрить. Но как показывает практика, благодаря словесно-логическим связкам человек запоминает информацию надолго, и не только математическую.
‘);> //–>
Тригонометрия – это раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии.
Синус (sin) – это тригонометрическая функция, геометрически представляющая отношение противолежащего катета к гипотенузе в прямоугольном треугольнике.
Косинус (cos) – это тригонометрическая функция, геометрически представляющая отношение прилежащего катета к гипотенузе в прямоугольном треугольнике.
Перевод синуса в косинус и обратно выполняется посредством решения основного тригонометрического тождества sin 2 (x) + cos 2 (x) = 1.
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор для перевода синуса в косинус (sin в cos). С помощью этого калькулятора вы в один клик сможете перевести косинус в синус (cos в sin) и обратно.
Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) – отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) – отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) – отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) – отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
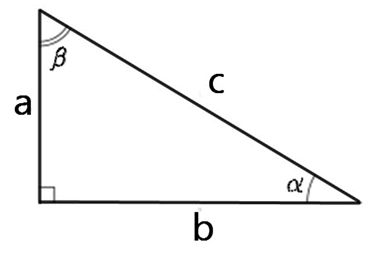
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Угол поворота
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Синус (sin) угла поворота
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс – основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Что такое sin в физике
Тригонометрия в физике.
Автор работы награжден дипломом победителя III степени
Актуальность: Данная тема, бесспорно, является актуальной. Тригонометрия использовалась людьми за много лет до нашей эры, уже тогда без знания этой науки было невозможно построить дом, а астрономам не удавалось провести различные расчеты. Спустя тысячелетия ничего не изменилось, тригонометрия по-прежнему остается одной из самых нужных наук, поэтому ее основы должен знать каждый человек, для того чтобы производить расчеты и иметь представление о самых элементарных функциях, так как тригонометрия заставляет думать логически и концентрирует наше внимание.
Цель: Определение связи тригонометрии с окружающим миром.
1.Рассмотреть историю возникновения и развития тригонометрии.
2.Показать на примерах практическое применение тригонометрии в физике.
3.Раскрыть на примерах возможности использования тригонометрических функций.
Гипотеза: Большинство физических явлений природы, физиологических процессов, закономерностей в музыке и искусстве можно описать с помощью тригонометрии и тригонометрических функций.
Практическая значимость: проект может использоваться в качестве теоретического курса в качестве дополнения, закрепления уже пройденного материала или на внеурочных занятиях.
1.История возникновения тригонометрии
Зачатки тригонометрии можно найти в математических рукописях древнего Египта, Вавилона и древнего Китая. 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.
От вавилонской математики ведёт начало привычное нам измерение углов градусами, минутами и секундами (введение этих единиц в древнегреческую математику обычно приписывают Гипсиклу, II век до н. э.).
Среди известных вавилонянам теорем была, например, такая: вписанный угол, опирающийся на диаметр круга — прямой. Главным достижением этого периода стало соотношение, позже получившее название теоремы Пифагора. Неизвестно, знали ли общую формулировку теоремы древние египтяне, но прямоугольный «египетский треугольник» со сторонами 3, 4 и 5 был там хорошо известен и широко использовался.
Общее и логически связное изложение тригонометрических соотношений появилось в древнегреческой геометрии. Греческие математики ещё не выделяли тригонометрию как отдельную науку, для них она была частью астрономии. Впервые само слово тригонометрия встречается в 1505 году в заглавии книги немецкого математика Питискуса.
Основным достижением античной тригонометрической теории стало решение в общем виде задачи «решения треугольников», то есть нахождения неизвестных элементов треугольника, исходя из трёх заданных его элементов (из которых хотя бы один является стороной).
В данном случае измерение треугольников следует понимать как решение треугольников, т. е. определение сторон, углов и других элементов треугольника, если даны некоторые из них.
Возникновение тригонометрии связано с землемерением, астрономией и строительным делом.
Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10′ с точностью до 1/604. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.
Долгое время тригонометрия носила чисто геометрический характер, т. е. Факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Пожалуй, наибольшие стимулы к развитию тригонометрии возникали в связи с решением задач астрономии, что представляло большой практический интерес.
Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.
Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Громадное научное наследие Эйлера включает блестящие результаты, относящиеся к математическому анализу, геометрии, теории чисел, механике и другим приложениям математики. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее проще.
Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.
Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс, котангенс, секанс и косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция.
Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OМ и положительным направлением оси Ox равен α.
Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r:
sinα=y/r.
Поскольку r=1, то синус равен ординате точки M(x,y).
Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r:
cosα=x/r
Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x:
tanα=y/x,x≠0
Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
cotα=x/y,y≠0
Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y):
secα=r/x=1/x,x≠0
Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y):
cscα=r/y=1/y,y≠0
В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
Синусом угла α называется отношение противолежащего катета к гипотенузе.
Косинусом угла α называется отношение прилежащего катета к гипотенузе.
Тангенсом угла α называется противолежащего катета к прилежащему.
Котангенсом угла α называется прилежащего катета к противолежащему.
Секанс угла α представляет собой отношение гипотенузы к прилежащему катету.
Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету.
График функции синус
y=sinx, область определения: x∈R, область значений: −1≤sinx≤1
График функции косинус
y=cosx, область определения: x∈R, область значений: −1≤cosx≤1
График функции тангенс y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞
Старт в науке
Учредителями Конкурса являются Международная ассоциация учёных, преподавателей и специалистов – Российская Академия Естествознания, редакция научного журнала «Международный школьный научный вестник», редакция журнала «Старт в науке».
Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Угол поворота
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Синус (sin) угла поворота
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Основные функции тригонометрии
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Что такое синус
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о том, что такие СИНУС.
Наверняка многие знают, что это понятие относится к математике. Все мы учились в школе и проходили тригонометрию.
С понятиями СИНУС, КОСИНУС, ТАНГЕНС и КОТАНГЕНС школьники знакомятся в 8 классе.
И сейчас без этих знаний не обойтись на ЕГЭ. И задачки по тригонометрии обязательно входят в программу тестов единого государственного экзамена.
Так что эта статья будет в первую очередь полезна старшеклассникам. А читателям более старшего возраста будет полезно лишний раз освежить давно забытые знания.
Что такое тригонометрия
Но давайте начнем совсем с азов. Раз уж мы сказали, что СИНУС – это некая тригонометрическая функция, давайте расскажем и что такое тригонометрия.
Тригонометрия – это раздел математики, который был основан еще в Древней Греции. Само слово состоит из двух половин «τρίγωνον» и «μετρέω», что можно дословно перевести как «изучение треугольников».
Впервые нечто похожее на тригонометрические функции появилось в Древней Греции. Во всяком случае, их можно отследить по трудам Евклида и Архимеда, то есть в III веке до нашей эры.
Хотя ученые не исключают, что похожими вычислениями пользовались и при строительстве Египетских пирамид. А это уже 2-2,5 тысячи лет до нашей эры.
И опять же, пирамиды ведь имеют треугольную форму (в плоскости). И тригонометрия связана напрямую с треугольниками. Возможно совпадение, а возможно и нет.
Правда, в тригонометрии рассматривают конкретные треугольники – прямоугольные. Напомним, это такие фигуры, у которых две стороны из трех пересекаются друг с другом под углом 90 градусов.
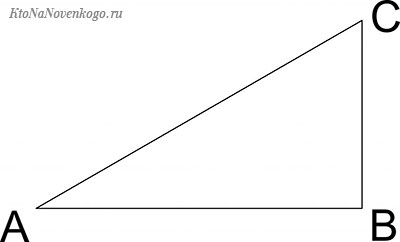
Выглядит такой треугольник вот так:
У такого треугольника стороны имеют определенные названия:
КАТЕТЫ – это стороны, которые пересекаются под прямым углом.
В нашем случае это стороны АВ и ВС. Это название также имеет древнегреческие корни. Так, слово «káthetos» переводится как «перпендикуляр, опущенный, ответственный».
ГИПОТЕНУЗА – сторона, которая идет под наклоном и соединяет между собой два катета.
В нашем случае это отрезок АС. Слово также родом из Древней Греции, «ὑποτείνουσα» означает «натянутая». И это очень хорошо характеризует этот отрезок, ведь он действительно выглядит как натянутая струна между двух опор. И даже если перевернуть треугольник, это ощущение не изменится.
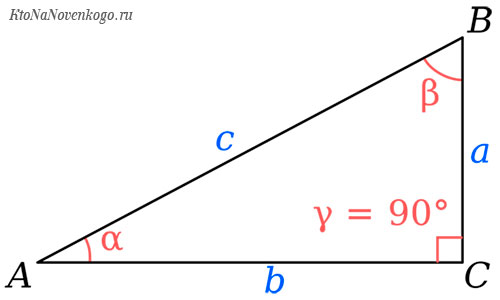
А вот теперь мы подобрались к самому главному, определению СИНУСА. Это величина не существует сама по себе. Она имеет отношение к какому-то углу треугольника. А конкретно к углам α (альфа) и β (бета), которые наглядно показаны на следующем рисунке.
А вот теперь долгожданное определение:
СИНУС угла – это отношение противолежащего катета к гипотенузе.
Чтобы было понятно, о чем речь, взгляните еще раз на наш рисунок прямоугольного треугольника. В данном случае, противолежащим катетом к углу α будет сторона ВС. А противолежащим катетом к углу β будет сторона АС.
Соответственно, катет ВС для угла α будет прилежащим. И точно таким же будет катет ВС для угла β.
Конкретные формулы синусов будут такими:
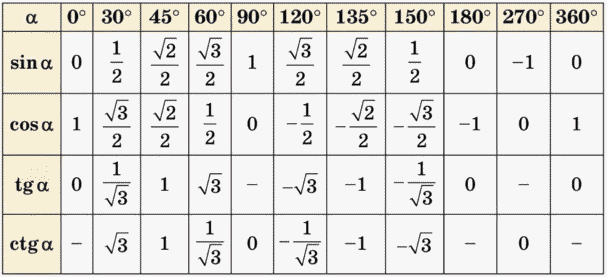
Значения синусов
Чаще всего школьники имеют дело с определенными углами. Например, 30, 45, 60, 90 градусов и так далее. И чтобы не высчитывать каждый раз значение тригонометрических функций через стороны треугольника, есть уже готовые таблицы:
Вместо заключения
СИНУС – это не единственная тригонометрическая функция, которую проходят в школе. Есть еще и другие, и все они также связаны с прямоугольным треугольником.
А называются они вот так:
Вот и все, что мы хотели рассказать о тригонометрической функции СИНУС.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (3)
Вот я вроде школу давно окончил, а вот все равно помню все. Потому что учили нас на совесть, а не спустя рукава. Вот скажите мне, а где в школах есть такое, что если ученик не понял, то учитель был готов потратить на него субботу и воскресенье чтобы объяснить дополнительно? Именно поэтому даже ярые троешники что-то знали.
Сейчас если ты в школе не понял, то все. Я дочери сам объяснял все по синусам, хотя и не учитель вообще. И кстати в современных учебниках материал очень плохо подан. Качаю старые советские, там куда понятнее. У вас кстати в статье хорошо рассказано. Я кстати в свое время так и запоминал, что это противоположный катет к гипотенузе.
Вспомнить никогда не будет лишним. Согласна с вами, Владимир, учили нам на совесть, спасибо нашим учителям.
«Соответственно, катет ВС для угла α будет прилежащим.»
Ошибка, для угла α прилежащим будет катет AC!