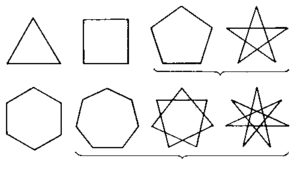
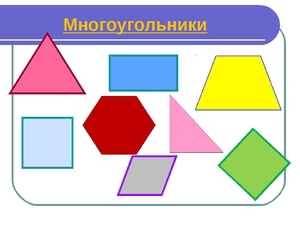
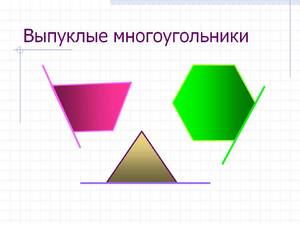
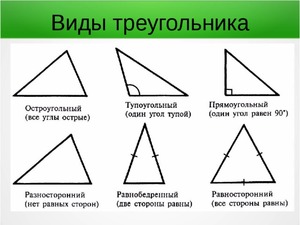
Что такое n угольник 8 класс определение
Многоугольник
Многоуго́льник — это геометрическая фигура, обычно определяется как замкнутая ломаная,имеющая больше одного угла.
Существуют три различных варианта определения многоугольника:
В любом случае, вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.
Содержание
Связанные определения
Виды многоугольников
Свойства
Вариации и обобщения
Планигон
Полезное
Смотреть что такое «Многоугольник» в других словарях:
многоугольник — многоугольник … Орфографический словарь-справочник
МНОГОУГОЛЬНИК — (на плоскости) геометрическая фигура, ограниченная замкнутой ломаной линией, звенья которой называются сторонами многоугольника, а их концы вершинами многоугольника. По числу вершин различают треугольники, четырехугольники и т. д. Многоугольник… … Большой Энциклопедический словарь
МНОГОУГОЛЬНИК — МНОГОУГОЛЬНИК, плоская геометрическая фигура с тремя или более сторонами, пересекающимися в трех или более точках (вершинах). Они называются в соответствии с числом сторон или вершин: ТРЕУГОЛЬНИК (трехсторонний); ЧЕТЫРЕХУГОЛЬНИК… … Научно-технический энциклопедический словарь
многоугольник — полигон Словарь русских синонимов. многоугольник сущ., кол во синонимов: 12 • восьмиугольник (3) • … Словарь синонимов
МНОГОУГОЛЬНИК — МНОГОУГОЛЬНИК, многоугольника, муж. (мат.). Плоская фигура, ограниченная тремя, четырьмя и т.д. прямыми линиями. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
МНОГОУГОЛЬНИК — МНОГОУГОЛЬНИК, а, муж. В математике: геометрическая фигура, ограниченная замкнутой ломаной линией. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Многоугольник — Многоугольник. В элементарной геометрии М. называется фигура,ограниченная прямыми линиями, называемыми сторонами. Точки, в которыхстороны пересекаются, называются вершинами. Число вершин равняется числусторон. Смотря по этому числу, М. называются … Энциклопедия Брокгауза и Ефрона
многоугольник — (напр. сил) [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN polygon … Справочник технического переводчика
многоугольник — а; м. Геометрическая фигура, ограниченная ломаной линией, звенья которой образуют более четырёх углов. Правильный м. Сторона многоугольника. * * * многоугольник (на плоскости), геометрическая фигура, ограниченная замкнутой ломаной линией, звенья… … Энциклопедический словарь
Геометрическая фигура многоугольник
Многоугольником называется геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией. При этом количество звеньев ломаной не должно быть меньше трех. Каждая пара отрезков ломаной имеет общую точку и образует углы. Количество углов совместно с количеством отрезков ломаной являются основными характеристиками многоугольника. В каждом многоугольнике количество звеньев ограничивающей замкнутой ломаной совпадает с количеством углов.
Сторонами в геометрии принято называть звенья ломаной линии, которая ограничивает геометрический объект. Вершинами называют точки соприкосновения двух соседних сторон, по количеству которых получают свои названия многоугольники.
Если замкнутая ломаная состоит из трех отрезков, она носит название треугольника; соответственно, из четырех отрезков — четырехугольником, из пяти — пятиугольником и пр.
Для обозначения треугольника или четырехугольника пользуются заглавными латинскими буквами, обозначающими его вершины. Буквы называют по порядку — по часовой стрелке или против нее.
Основные понятия
Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:
Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:
Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.
Виды фигур
Треугольник
Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.
Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.
По соотношениям между сторонами все треугольники можно подразделять на несколько видов:
Кроме того, принято различать следующие треугольники:
Четырехугольник
Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.
На одной прямой не может находиться сразу три вершины четырехугольника.
Видео
Дополнительную информацию о многоугольниках вы найдете в этом видео.
» width=»560″ height=»314″ allowfullscreen=»allowfullscreen»>Многоугольник
Определение 1. Многоугольник − замкнутая ломаная линия.
Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:
Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.
Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.
Виды многоугольников
Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.
    |
На рисунке 1 представлены различные виды многоугольников.
Обозначение многоугольника
Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).
Соседние вершины многоугольника
Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
 |
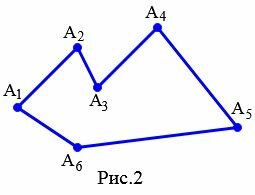На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)
Смежные стороны многоугольника
Стороны многоугольника называются смежными, если они имеют общую вершину.
На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)
Простой многоугольник. Самопересекающийся многоугольник
Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
  |
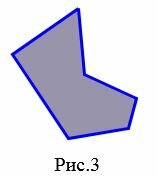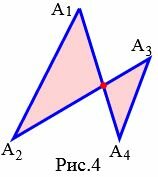На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.
Выпуклый многоугольник
Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
 |
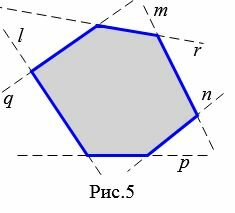На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.
 |
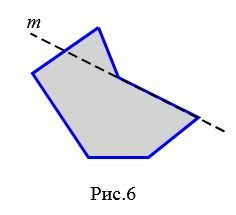На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.
Правильный многоугольник
Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.
  |
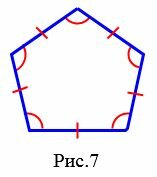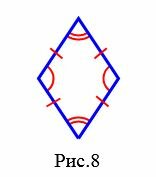На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Звездчатый многоугольник
Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.
 |
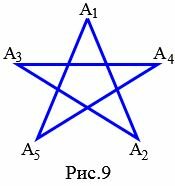На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)
Периметр многоугольника
Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_
Угол многоугольника
Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).
Внешний угол многоугольника
Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.
На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)
Диагональ многоугольника. Количество диагоналей
Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.
Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:
Сумма углов выпуклого многоугольника
Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_
 |
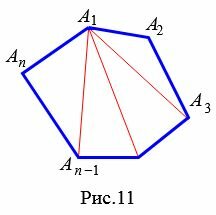Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)
где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.
Угол правильного многоугольника
Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:
где \( \small n \) −количество сторон (вершин) правильного многоугольника.
8 класс. Геометрия. Многоугольники.
8 класс. Геометрия. Многоугольники.
Вопросы
Задай свой вопрос по этому материалу!
Поделись с друзьями
Комментарии преподавателя
Многоугольники
1. Понятие «многоугольник»
В курсе геометрии мы изучаем свойства геометрических фигур и уже рассмотрели простейшие из них: треугольники и окружности. При этом мы обсуждали и конкретные частные случаи этих фигур, такие как прямоугольные, равнобедренные и правильные треугольники. Теперь пришло время поговорить о более общих и сложных фигурах – многоугольниках.
С частным случаем многоугольников мы уже знакомы – это треугольник (см. Рис. 1).
В самом названии уже подчеркивается, что это фигура, у которой три угла. Следовательно, в многоугольнике их может быть много, т.е. больше, чем три. Например, изобразим пятиугольник (см. Рис. 2), т.е. фигуру с пятью углами.
Рис. 2. Пятиугольник. Выпуклый многоугольник
Определение.Многоугольник – фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются вершинами многоугольника, а отрезки – сторонами. При этом никакие две смежные стороны не лежат на одной прямой и никакие две несмежные стороны не пересекаются.
Определение.Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны.
Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю. Внутреннюю область также относят кмногоугольнику.
Иными словами, например, когда говорят о пятиугольнике 
, имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника, т.е. точка 
тоже относится к пятиугольнику (см. Рис. 2).
Многоугольники еще иногда называют n-угольниками, чтобы подчеркнуть, что рассматривается общий случай наличия какого-то неизвестного количества углов (n штук).
Определение. Периметр многоугольника – сумма длин сторон многоугольника.
Теперь надо познакомиться с видами многоугольников. Они делятся на выпуклые и невыпуклые. Например, многоугольник, изображенный на Рис. 2, является выпуклым, а на Рис. 3 невыпуклым.
Рис. 3. Невыпуклый многоугольник
2. Выпуклые и невыпуклые многоугольники
Определение 1. Многоугольник называется выпуклым, если при проведении прямой через любую из его сторон весь многоугольник лежит только по одну сторону от этой прямой. Невыпуклыми являются все остальные многоугольники.
Легко представить, что при продлении любой стороны пятиугольника на Рис. 2 он весь окажется по одну сторону от этой прямой, т.е. он выпуклый. А вот при проведении прямой через 
в четырехугольнике на Рис. 3 мы уже видим, что она разделяет его на две части, т.е. он невыпуклый.
Но существует и другое определение выпуклости многоугольника.
Определение 2. Многоугольник называется выпуклым, если при выборе любых двух его внутренних точек и при соединении их отрезком все точки отрезка являются также внутренними точками многоугольника.
Демонстрацию использования этого определения можно увидеть на примере построения отрезков 
на Рис. 2 и 3.
Определение. Диагональю многоугольника называется любой отрезок, соединяющий две не соседние его вершины.
3. Теорема о сумме внутренних углов выпуклого n-угольника
Для описания свойств многоугольников существуют две важнейшие теоремы об их углах: теорема о сумме внутренних углов выпуклого многоугольника и теорема о сумме внешних углов выпуклого многоугольника. Рассмотрим их.
Теорема. О сумме внутренних углов выпуклого многоугольника (n-угольника).
, где 
– количество его углов (сторон).
Доказательство 1. Изобразим на Рис. 4 выпуклый n-угольник.
Рис. 4. Выпуклый n-угольник
Из вершины 
проведем все возможные диагонали. Они делят n-угольник на 
треугольника, т.к. каждая из сторон многоугольника образует треугольник, кроме сторон, прилежащих к вершине . Легко видеть по рисунку, что сумма углов всех этих треугольников как раз будет равна сумме внутренних углов n-угольника. Поскольку сумма углов любого треугольника – 
, то сумма внутренних углов n-угольника:
, что и требовалось доказать.
Доказательство 2. Возможно и другое доказательство этой теоремы. Изобразим аналогичный n-угольник на Рис. 5 и соединим любую его внутреннюю точку со всеми вершинами.
Мы получили разбиение n-угольника на n треугольников (сколько сторон, столько и треугольников). Сумма всех их углов равна сумме внутренних углов многоугольника и сумме углов при внутренней точке, а это угол 
. Имеем:
, что и требовалось доказать.
По доказанной теореме видно, что сумма углов n-угольника зависит от количества его сторон (от n). Например, в треугольнике 
, а сумма углов 
. В четырехугольнике 
, а сумма углов – 
и т.д.
4. Теорема о сумме внешних углов выпуклого n-угольника
Теорема. О сумме внешних углов выпуклого многоугольника (n-угольника).
, где – количество его углов (сторон), а 
, …, 
– внешние углы.
Доказательство. Изобразим выпуклый n-угольник на Рис. 6 и обозначим его внутренние и внешние углы.
Рис. 6. Выпуклый n-угольник с обозначенными внешними углами
Т.к. внешний угол связан со внутренним как смежные, то 
и аналогично для остальных внешних углов. Тогда:
.
В ходе преобразований мы воспользовались уже доказанной теоремой о сумме внутренних углов n-угольника 
.
Из доказанной теоремы следует интересный факт, что сумма внешних углов выпуклого n-угольника равна 
от количества его углов (сторон). Кстати, в отличие от суммы внутренних углов.
Далее мы более подробно будем работать с частным случаем многоугольников – четырехугольниками. На следующем уроке мы познакомимся с такой фигурой, как параллелограмм, и обсудим его свойства.