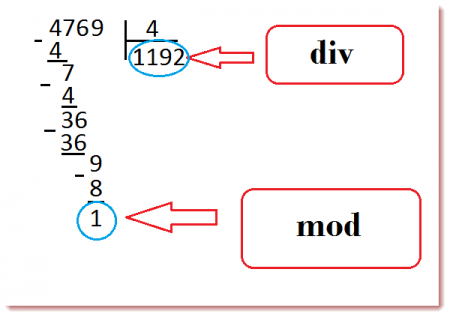
Что такое mod в математике
Что такое mod в математике
Оператор div и оператор mod
В этой статье речь пойдет о целочисленном делении и делении с остатком.
То есть например 20 / 5 = 4, 55 / 6 = 9, 100 / 3 = 33 и т.д.
Согласитесь, что в некоторых случаях это очень удобно и практично. Теперь поговорим о реализации этого метода в Паскале. Тут все достаточно просто, открывать Америку не придется. В паскале за целочисленное деление отвечает оператор div. Теперь как это записывается в Pascal’e
Таким образом, вот такая запись (55 / 6) нацело = 9 в результате использования оператора div будет выглядеть так
z будет равно 9. Запомните! При использовании оператора div дробная часть будет отброшена!
А сейчас поговорим о делении с остатком. Оно не особо отличается и главным здесь является то, что в результате отбрасывается как раз целая часть. То есть (40 / 6) с остатком = 4, (10 / 3) с остатком =1, (22 /5) с остатком = 2 и т.д. В паскале для этого есть оператор mod. Записывается он точно так же.
Например (40 / 6) с остатком = 4 с оператором mod будет такой
Кстати оператор mod часто используют, для определения кратности чисел (кратность — это делимость на какое-нибудь число нацело. То есть например говорят, что числа 3, 6, 9, 12, 21 кратны трем. Или числа 5,10,15,20 кратны 5). В статье нахождение четных элементов массива я упоминал о числах кратных двум (четных). Итак как эту кратность определить в паскале. Обратите внимание, что если число кратное, то у него есть остаток (точнее оно имеет в остатке ноль). Этим и стоит воспользоваться.
Сейчас я привел пример условия, которое проверяет кратность, где v — это число, проверяемое на кратность по числу m. Например чтобы проверить,
является ли 40 кратным 4, используем оператор mod с условием и получим
Mod и остаток — не одно и то же
Приготовьтесь, вас ждёт крайне педантичная статья, которая вполне может спасти вас на собеседовании или сэкономить несколько часов при вылавливании бага в продакшне!
Я сейчас активно работаю над вторым сезоном «Руководства для самозванца» и пишу о шифре RSA для SSH, который, очевидно, является самым загружаемым фрагментом кода в истории IT.
Хочется полностью разобраться в этой истории. Кто придумал этот шифр, как он работает, почему работает и будет ли работать в будущем. Сейчас я раскопал одну чертовски интересную историю. Я не криптоманьяк и вижу, как других буквально засасывает в эту область. Но мне это тоже интересно, потому что повсюду есть маленькие норки, а меня как сороку привлекают блестящие штучки в глубоких норках. Я также очень хорош в метафорах.
В любом случае: на прошлой неделе я узнал что-то странное и хочу поделиться: оказывается, mod и остаток от деления — не одно и то же. Действительно забавно то, что некоторые читатели при этих словах выпрыгивают со своих кресел и орут: «А ведь именно это я всегда пытался сказать вам и всем остальным!»
Позовите ребят из секты «mod не остаток»! Это для вас.
Что такое mod?
Я должен был изучить это, как и в прошлый раз, когда всплыла такая тема. Это одна из тех вещей, которые ты знаешь, но не запоминаешь. Когда вы применяете mod, то делите одно число на другое и берёте остаток. Итак: 5 mod 2 будет 1, потому что 5/2=2 с остатком 1.
Вот где мы попадаем в странную серую область.
Математика циферблата
Криптографам нравится эта идея, потому что они могут использовать деление с остатком с гигантскими простыми числами для генерации криптографических ключей. Это совсем другая история: если хотите прочитать об этом, то можете купить книгу или, ещё лучше, поддержать мои усилия написать её.
Впрочем, не будем отклоняться от темы.
Остатки и математика циферблата
Теперь переходим к сути: modulo и простой остаток одинаковы, когда числа положительны, но отличаются в случае отрицательных чисел.
Рассмотрим такую задачу:
JavaScript с этим согласен:
Google согласен с первым утверждением, но не согласен со вторым:
Ruby согласен с Google:
Во имя Дейкстры, что здесь происходит?
Вращение часов назад
Чтобы ответить на вопрос, следует понять разницу между остатком и modulo. Программисты объединяют эти операции, но не должны этого делать, потому что они дают одинаковый результат только в случае, если делитель (в нашем случае 12) положителен. Вы можете легко отправить баги в продакшн, если делитель отрицательный.
Но почему существует разница? Рассмотрим положительный делитель 19 mod 12 на часах:
Это известная вещь
Прежде чем назвать меня сумасшедшим и начать гуглить тему: это известный факт. На самом деле MDN (Mozilla Developer Network) даже дошла до того, чтобы назвать % операцией «остатка» (remainder), а не modulo:
Оператор remainder возвращает остаток от деления одного операнда на другой. Он всегда принимает знак делимого.
Вот что Эрик Липперт, один из богов C#, говорит о modulo в C#:
Однако это совсем не то, что оператор % реально делает в C#. Оператор % не является каноническим оператором modulus, это оператор остатка.
А как на вашем языке?
Ну и что?
Могу понять, если вы дочитали досюда, а теперь чешете голову и задаётесь вопросом, стоит ли беспокоиться. Думаю, что стоит по двум причинам:
[математикам]что такое mod?
в методичке по криптографии постоянно встречаются формулы вида этой:
Что такое mod? Простой остаток от деления e^-1 на p-1?
Судя по всему нет, т.к. вот пример из той же методички:
d = e^-1 (mod p-1) = 42239^-1 (mod(52631-1) = 32229
p.s. Да, математика в институте была >5 лет назад, и она вовсе не мой конек.
Re: [математикам]что такое mod?
а вроде всегда это был остаток от деления. число, не превосходящее делитель.
Re: [математикам]что такое mod?
//читаю лекции по криптографии у людей с большими провалами в математике, даже поля Галуа и теорему Ейлера можно объяснить на пальцах, ящитаю
Re: [математикам]что такое mod?
про (mod p-1) уже сказали, но
> d = e^-1 (mod p-1) = 42239^-1 (mod(52631-1) = 32229
либо очепятка, либо ошибка:
a^<-1>=b(mod c) если a*b=1(mod c), но у тут
Re: [математикам]что такое mod?
Re: [математикам]что такое mod?
Ужас. Закрывай методичку, открывай теорию чисел. А то что будет, когда дискретные логарифмы (ЕМНИП, ГОСТовское шифрование на них основано, но тут могу ошибаться, лет 10 криптографию не трогал) встретишь и т.д.
Re: [математикам]что такое mod?
ОМГ, так это ты подпускаешь людей без знания математики к криптографии?
Re: [математикам]что такое mod?
> //читаю лекции по криптографии у людей с большими провалами в математике, даже поля Галуа и теорему Ейлера можно объяснить на пальцах, ящитаю
Объясните на пальцах БПФ. Не что он делает, а КАК.
Ну мля, я хочу понять, как всё-таки эти формулы с интегралами в циклы расписать чтобы ему на вход массив с PCM, на выходе массив с частотами.
Re: [математикам]что такое mod?
Здесь либо порядок операций нужно смотреть, либо ограничение представления машинного числа в памяти компа. Положительное integer принимает значения от 0 до 32767. Ну, типа тогда 0-1=32767.
Re: [математикам]что такое mod?
Ну что такое остаток я понимаю, но как его найти в данном примере? Ведь e^ <-1>явно меньше чем (p-1)?
p.s. эта формула из «трехподходного протокола Шамира»
Re: [математикам]что такое mod?
Самое простое объяснение: в методичке опечатка, пропущена какая-то буква перед «-1».
Re: [математикам]что такое mod?
Re: [математикам]что такое mod?
Это таки точно опечатка. У меня получается 34229, что слишком похоже на 32229, чтобы быть случайным.
Re: [математикам]что такое mod?
Т.е. получается: d = e^ <-1>(mod p-1) = 42239^ <-1>(mod(52631-1) = 34229
Еще раз, для малограмотных, объясните как взять остаток от деления 42239^ <-1>= 2.36748029073e-05 на 52630?
Re: [математикам]что такое mod?
>как взять остаток от деления 42239^
Re: [математикам]что такое mod?
Спасибо, тогда тоже пока напишу скрипт, пусть ищет.
Деление чисел с остатком
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Деление с остатком целых положительных чисел
Деление — это разбиение целого на равные части.
Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.
Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!
Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.
Попрактикуемся в решении.
Пример
Разделить 14671 на 54.
Выполним деление столбиком:
Неполное частное равно 271, остаток — 37.
Ответ: 14671 : 54 = 271(остаток 37).
Деление с остатком положительного числа на целое отрицательное
Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:
В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.
Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.
Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».
Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.
Алгоритм деления положительного числа на целое отрицательное (с остатком):
Пример
Разделить 17 на −5 с остатком.
Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.
Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.
Ответ: 17 : (− 5) = −3 (остаток 2).
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Деление с остатком целого отрицательного числа на целое положительное
Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:
Чтобы получить неполное частное с при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток d будет вычисляться по формуле:
d = a − b * c
Из правила делаем вывод, что при делении получается целое неотрицательное число.
Для точности решения применим алгоритм деления а на b с остатком:
Рассмотрим пример, где можно применить алгоритм.
Пример
Найти неполное частное и остаток от деления −17 на 5.
Разделим заданные числа по модулю.
Получаем, что при делении частное равно 3, а остаток 2.
Так как получили 3, противоположное ему −3.
Необходимо отнять единицу: −3 − 1 = −4.
Чтобы вычислить остаток, необходимо a = −17, b = 5, c = −4, тогда:
d = a − b * c = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.
Значит, неполным частным от деления является число −4 с остатком 3.
Ответ: (−17) : 5 = −4 (остаток 3).
Деление с остатком целых отрицательных чисел
Сформулируем правило деления с остатком целых отрицательных чисел:
Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:
d = a − b * c
Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.
Алгоритм деления с остатком целых отрицательных чисел:
Пример
Найти неполное частное и остаток при делении −17 на −5.
Применим алгоритм для деления с остатком.
Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.
Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.
Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим d = a − b * c = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.
Получилось, что остаток равен 3, а неполное частное равно 4.
Ответ: (−17) : (−5) = 4 (остаток 3).
Деление с остатком с помощью числового луча
Деление с остатком можно выполнить и на числовом луче.
Пример 1
Рассмотрим выражение: 10 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.
Решение: 10 : 3 = 3 (остаток 1).
Пример 2
Рассмотрим выражение: 11 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.
Решение: 11 : 3 = 3 (остаток 2).
Проверка деления с остатком
Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.
Формула деления с остатком
a = b * c + d,
где a — делимое, b — делитель, c — неполное частное, d — остаток.
Эту формулу можно использовать для проверки деления с остатком.
Пример
Рассмотрим выражение: 15 : 2 = 7 (остаток 1).
В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.
Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:
Теорема о делимости целых чисел с остатком
Если нам известно, что а — это делимое, тогда b — это делитель, с — неполное частное, d — остаток. И они между собой связаны. Эту связь можно описать через теорему о делимости с остатком и показать при помощи равенства.
Теорема
Любое целое число может быть представлено только через целое и отличное от нуля число b таким образом:
где q и r — это некоторые целые числа. При этом 0 ≤ r ≤ b.
Доказательство:
Если существуют два числа a и b, причем a делится на b без остатка, тогда из определения следует, что есть число q, и будет верно равенство a = b * q. Тогда равенство можно считать верным: a = b * q + r при r = 0.
Тогда необходимо взять q такое, чтобы данное неравенством b * q
Оператор Mod (Visual Basic)
Делит два числа и возвращает только остаток.
Синтаксис
Компоненты
result
Обязательный элемент. Любая числовая переменная или свойство.
number1
Обязательный. Произвольное числовое выражение.
number2
Обязательный. Произвольное числовое выражение.
Поддерживаемые типы
Результат
Remarks
Если number1 или number2 имеет значение Nothing, оно считается нулевым.
К связанным операторам относятся следующие.
оператор \ (Visual Basic) возвращает целочисленное частное от деления. Например, выражение принимает значение 14 \ 4 3.
оператор/(Visual Basic) возвращает полное частное, включая остаток, в виде числа с плавающей запятой. Например, 14 / 4 результатом вычисления выражения является 3,5.
Попыток деления на ноль
Если number2 значение равно нулю, поведение Mod оператора зависит от типа данных операндов:
Эквивалентная формула
Выражение a Mod b эквивалентно любой из следующих формул:
Точность чисел с плавающей запятой
При работе с числами с плавающей запятой Помните, что они не всегда имеют точное десятичное представление в памяти. Это может привести к непредвиденным результатам некоторых операций, таких как сравнение значений и Mod оператор. Дополнительные сведения см. в разделе Устранение неполадок типов данных.
Перегрузка
Mod Оператор можно перегрузить, то есть класс или структура может переопределить его поведение. Если код применяется Mod к экземпляру класса или структуры, включающей такую перегрузку, убедитесь, что вы понимаете его переопределенное поведение. Для получения дополнительной информации см. Operator Procedures.
Пример 1
В следующем примере оператор используется Mod для деления двух чисел и возврата только остатка. Если любое число является числом с плавающей запятой, результатом является число с плавающей запятой, представляющее остаток.