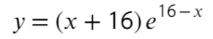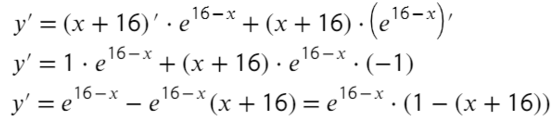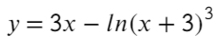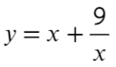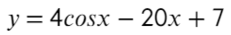Что такое max и min для функции
Как найти точки минимума и максимума функции
Минимум и максимум функции
Минимумом и максимумом функции, другими словами экстремумами, называют точки, в которых функция меняет характер монотонности (с возрастания на убывание и наоборот). Важно понимать, что экстремумы это не максимальные и минимальные значения функции. Обозначаются следующим образом:
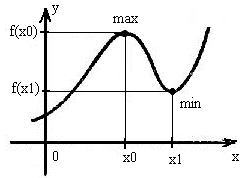
Точка минимума, минимум функции
Минимум функции — значение функции в точке минимума \(x_0\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Простыми словами, точка минимума — это та, где убывание функции меняется на возрастание.
Точка максимума, максимум функции
Максимум функции — значение функции в точке максимума \(x_0\)
Простыми словами, точка максимума — это та, где возрастание функции меняется на убывание.
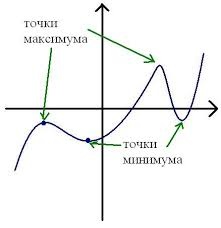
Точки максимума и минимума на графике:
Исследование функций на экстремумы
Теорема. Если функция f(x) имеет экстремум в точке \(x=x_0,\) то в ней производная либо равна 0, либо не существует.
Алгоритм нахождения экстремумов с помощью производной:
Найти область определения функции — D(y).
Определить производную — f ‘(x).
Исследовать характер изменения функции f (x) и знак f ‘(x) в промежутках, на которые найденные критические точки делят область определения (при отрицательном знаке производной функция убывает, при положительном — возрастает).
Относительно каждой критической точки определить, является ли она точкой максимума, минимума (возрастание меняется на убывание — точка максимума, убывание на возрастание — минимума) или не является точкой экстремума (то есть, меняется ли знак производной при переходе через исследуемую точку).
Вычислить значения функции в точках экстремума.
Примеры задач
Задача 1
Исследовать на экстремумы функцию \(f(x)=x^3-3x^2.\)
Решение задачи по алгоритму:
3) Из пункта 1 следует, что критических точек нет. Найдем стационарные:
5) Найдем значение экстремумов функции.
Задача 2
Задача 3
Докажите, что функция \(f(x)=x^5+2x^3-4\) возрастает на всех числовой прямой.
Максимум и минимум функции
Вы будете перенаправлены на Автор24
Одним из этапов исследования функции является нахождение экстремумов заданной функции, другими словами, максимума и минимума функции.
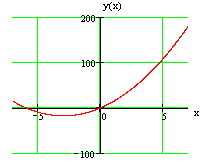
Точки экстремума показаны на рис.
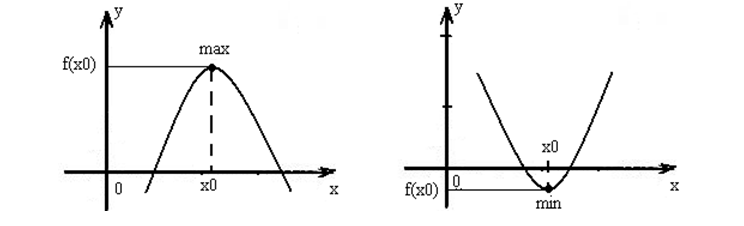
Экстремум параболы, рассматриваемой на всей области определения, совпадает с ее вершиной (рис.).
Значения заданной функции в точках минимума и максимума называются соответственно минимумом и максимумом заданной функции.
Экстремумы функции делятся на:
Определения 1 и 2 относятся к локальным экстремумам: локальный минимум и локальный максимум.
Наименьшее и наибольшее значения заданной функции на некотором промежутке являются глобальными экстремумами.
Глобальные экстремумы могут достигаться либо в точках локального экстремума, либо на концах отрезка.
Необходимое условие экстремума определяется следующей теоремой.
Готовые работы на аналогичную тему
Достаточные условия экстремума определяются следующими теоремами.
Алгоритм исследования заданной функции на экстремум включает следующие этапы:
Найдем критические и стационарные точки:
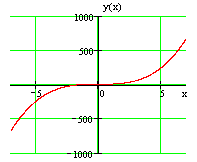
График заданной функции приведен на рис.
Найдем критические и стационарные точки:
$y(-3)=2\cdot (-3)^ <2>+12\cdot (-3)=2\cdot 9-36=18-36=-18$
График заданной функции приведен на рис.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 17 02 2021
Что такое max и min для функции
Значения функции и точки максимума и минимума

Наменьшее значение функции
Как говорил крестный отец: «Ничего личного». Только производные!
Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично.
12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.
12 задание бывает двух видов:
Найти точку максимума / минимума
Найдите точку максимума функции
Найдите точку минимума функции
Найти наибольшее / наименьшее значение функции
Найдите наибольшее значение функции на отрезке [−4; −1]
Найдите наибольшее значение функции на отрезке [0; 1,5π]
Максимумы, минимумы и экстремумы функций
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.
Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. \(y\). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, \(-5\) точка минимума (или точка экстремума), а \(1\) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось \(x\)).
Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.
Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди \(-13\), \(-11\), \(-9\),\(-7\) и \(3\).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.
\(-11\): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что \(-11\) – это минимум.
\(- 9\): функция возрастает, а потом убывает – максимум.
Все вышесказанное можно обобщить следующими выводами:
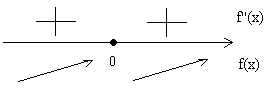
— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.
Пример(ЕГЭ). Найдите точку максимума функции \(y=3x^5-20x^3-54\).
Решение:
1. Найдем производную функции: \(y’=15x^4-60x^2\).
2. Приравняем её к нулю и решим уравнение:
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является \(-2\).
Наибольшее и наименьшее значение функции
Теория к заданию 12 из ЕГЭ по математике (профильной)
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.
Чтобы найти наибольшее или наименьшее значение функции необходимо:
Чтобы найти точки максимума или минимума необходимо:
Таблица производных некоторых элементарных функций:
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n, n∈N$ | $nx^ |
| $<1>/ | $-<1>/ |
| $<1>/x<^n>, n∈N$ | $- |
| $√^n | $<1>/ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | $<1>/ |
| $ctgx$ | $-<1>/ |
| $cos^2x$ | $-sin2x$ |
| $sin^2x$ | $sin2x$ |
| $e^x$ | $e^x$ |
| $a^x$ | $a^xlna$ |
| $lnx$ | $<1>/ |
| $log_x$ | $<1>/ |
Основные правила дифференцирования
1. Производная суммы и разности равна производной каждого слагаемого
Производная суммы и разности равна производной каждого слагаемого