Что такое google число

Машина для визуализации числа гугол

Гуго́л (от англ. googol) — число, в десятичной системе счисления изображаемое единицей со 100 нулями:

1 гугол = 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000

Eсли делать по одному обороту первого колеса в секунду, на это уйдет 317097919837645865043125317097919837645865043125317097919837645865043125317097919837645865043 лет, а если хотите обернутся по быстрому и уложиться лет в 25 скажем, то придется крутить со скоростью 12683916793505834601725012683916793505834601725012683916793505834601725012683916793505834601 оборотов в секунду

Видел в инторнете похожее видео, там куча шестерёнок, и последняя шестерёнка в бетоне. Не могу найти.

Можно ещё посчитать момент, который получается на 100-й шестерне и попробовать найти материал, что его выдержит.

Я бы к последней шестеренке приделал взрыватель термоядерной боеголовки, а на табличке написал что когда взрыватель сработает все радиоактивные материалы уже распадутся!

Гугл мелочь, число Грэма рулит, стопка степеней, если записывать ее шрифтом, каким я сейчас пишу, за пределы вселенной выйдет, во всяком случае если с моего стола записывать начать.

Техника из серии «материалы сгниют раньше чем будет достигнут результат»

Надо онлайн трансляцию этой машинки, засыпать самое то.

Вот ещё два варианта этой машинки. Первые шестерёнки быстрее сотрутся от трения, нежели повернётся замыкающая шестерня.

А можно мне такую зарплату?

Почему бы не сделать замок для сейфа из этой херни

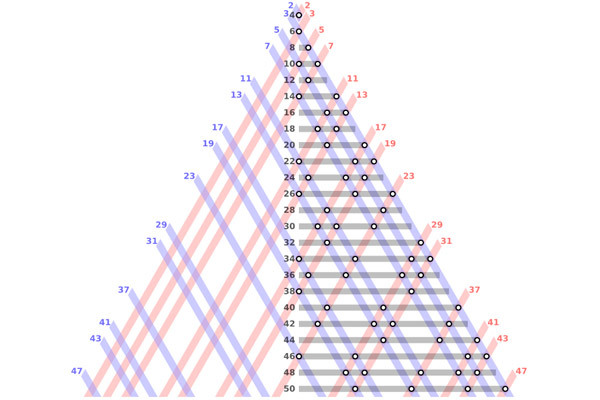
Признаки делимости

Я расскажу вам признаки делимости на все цифры. Но есть и составные, они чаще всего составлены из двух ЦИФР, при произведении их получится это число.

На 1: понятно, каждое число делится
На 2: последняя цифра четная
На 3: сумма всех цифр в числе делится на три
На 4: число, которое составляют две последние цифры либо 00, либо делится на 4
На 5: число оканчивается либо на 5, либо на 0
На 6: должны соблюдаться признаки делимости на 2 и на 3
На 7: это сложное правило, разберём на примере числа 259.
Сначала мы последнюю цифру удваиваем и убираем из числа. Затем из оставшегося числа (25)мы вычитаем произведение последней цифры на 2:
25-(2*9)=7. 7 делится на 7, значит и число тоже.
На 8: число, составленное из 3-х последних цифр должно делиться на 8 либо быть 000.
На 9: сумма всех цифр в числе должна делиться на 9.

День теоремы Пифагора

Сегодня, 16.12.2020, отмечается день теоремы Пифагора. Он отмечается лишь тогда, когда сумма квадратов даты и месяца равна квадрату года. 16² + 12² = 20²

Праздник бывает не каждый год. Предыдущий день был 15.08.2017, а следующий будет 24.07.2025.

Так вот оно что!

подыскиваю себе гараж по соседству с уже имеющимся. поэтому периодически почитываю объявления и позваниваю по ним. сегодня звоню по очередному объявлению.

— здравствуйте! гараж продаёте?

на том конце провода женский голос:

— ну у меня ещё один гараж есть, там цена на порядок меньше.

Это шутка?

Учительница начальных классов обожает свою работу и выкладывается по полной программе!

(На видео надпись: Когда в соседнем классе [работает/находится] учитель года.)

#1 Гипотеза Голдьбаха

Поэтому темой этой статьи будет именно гипотеза Голдьбаха

Так вот, в интернете я нашел книгу Энрике Грассия «Числа долгая дорога к бесконечности» в этой книге описывались особенности и история исследований простых чисел, именно там я нашел первое упоминание о гипотезе Голдьбаха

Затем в книжном магазине я набрёл на книгу Иэна Стюарта «Величайшие математические задачи» в которой также было упоминание про гипотезу Голдьбаха.

Гипотеза Голдьбаха была сформирована немецким математиком Христианом Гольдбахом и впервые описана в его письме Эйлеру.Условие гипотезы звучит так:

Но есть и тернарная часть данной гипотезы которая звучит так:Любое нечётное число больше 5 можно представить в виде суммы трёх простых.

Для решения тернарой проблемы Математики использовали так называемый метод перекрытия.

Этот метод значительно снизил диапазон простых чисел,а значит и пространство исследования.Позже Шнерельманом была сформирована постоянная что некое число C равно сумме некоторого n чисел

В 1990х годах Оливье Рамаре доказал что постоянная равна 6.И только в 2013 году математик из Перу доказал гипотезу Голдьбаха снизив постоянную с шести до 4 и использовав теорию вероятностей.

Но бинарная гипотеза Гольдбаха до сих пор не решена

1.О гипотезе Голдьбаха написан Роман дядя Петрос и гипотеза Гольдбаха в центре сюжета история математика который пытается доказать гипотезу.

2.За решение гипотезы Гольдбаха Корнельский университет платит 5 млн долларов США

Источник

Самые большие числа и какое число идет после гугла

Знаете, какое число идет после гугла? Слово «гугол» получило широкое распространение благодаря всем известной компании и одноименной поисковой системе. Однако в названии поисковика это слово используется в немного измененной форме.

Какие интересные числа есть до гугла

Далее можно приводить еще много чисел, но их все сложнее и сложнее представить, потому что сложно найти пример, который бы их описывал. Но все же такие числа люди еще «слышат» раз через раз, например:

квадриллион — 10 в 15-й степени;

квинтиллион — 10 в 18-й степени;

секстиллион — 10 в 21-й степени;

септиллион — 10 в 24-й степени;

октиллион — 10 в 27-й степени;

нониллион — 10 в 30-й степени;

Какое число идет после гугла

Гуголплекс. Это число обозначает 10, возведенн ое в степень гугол, то есть 10, возведенное в число степен и со 100 знаками. Это число является попыткой измерить количество частиц во всей Вселенной.

Число Скьюза. Это число показывает верхний предел для математических вычислений. Считается, что числа больше числа Скьюза нарушают многие математические правила и ведут себя по-другому. Даже самое меньшее число Скьюза будет намного больше г у голплекса и обозначается как: 10˄10˄10˄36, где ˄ — это возведение в степень.

Заключение

Мы будем очень благодарны

если под понравившемся материалом Вы нажмёте одну из кнопок социальных сетей и поделитесь с друзьями.

Источник

Наглядный пример того, как выглядит число Google (видео)

Визуально представить самое большое число во Вселенной поможет механическая машина энтузиаста с YouTube Даниэля де Брюина, создавшего механизм с шестеренками, который объясняет и визуализирует число «гугол» или 10 в сотой степени. Такое число в настоящее время не имеет реальных аналогов, оно даже больше всего количества атомов в исследуемой части нашей Вселенной, которое составляет число приблизительно равное 10 в 81 степени.

Тем не менее тридцатилетний инженер смог визуализировать число, не имеющее аналогов в нашем мире. Свое изобретение Брюин приурочил к своему 30-ти летнему юбилею, отметив, что к этому времени уже прожил один миллиард секунд с момента рождения. Энтузиаст создал простой для понимания демонстратор числа «гугол» используя всего 100 шестерен с передаточным числом 10.

Соединенные последовательно 100 шестерен позволит придать хотя бы какой то физический смысл гигантскому числу «гугол», в свое время ставшее основой для названия гигантского поисковика Google. В настоящее время число 10 в 100 степени используется только теоретиками в математике больших чисел и не имеет практической пользы.

Демонстратор числа «гугол» использует принцип механической понижающей передачи, когда при 10 оборотах оной шестерни, другая поворачивается всего на один оборот. А для одного оборота третьей шестерни потребуется совершить уже 100 поворотов первой и 10 поворотов на второй шестерне. Таким образом, для поворота сотой шестеренки на один оборот, первая должна быть провернута «гугол» раз.

Источник

10 самых больших и важных чисел

Дети часто задают вопрос: «Какое число самое большое?». Этот вопрос — важный шаг в процессе перехода в мир абстрактных понятий. Ответ, конечно, прост: числа, скорее всего, бесконечны, но есть определенный порог, за которым числа становятся настолько большими, что в них нет смысла, кроме того, что технически они могут существовать. Давайте возьмем десятку гигантских чисел, известных нам, но ограничимся крайне важными понятиями в мире чисел.

Десять в восьмидесятой степени — 1 с 80 нулями — это довольно массивное число, обозначающее примерное число элементарных частиц в известной вселенной, и, говоря элементарные частицы, мы не имеем в виду микроскопические частицы — мы говорим о куда меньших вещах вроде кварков и лептонов — о субатомных частицах. Это число в США и современной Великобритании называют «сто квинквавигинтиллионов». Вроде бы, несложно понять, что это число обозначает количество мельчайших частиц в нашей Вселенной, однако это самое маленькое и простое число в нашем списке.

Один гугол

Слово гугол, несколько измененное, стало часто используемым в современности, благодаря популярной поисковой системе. У этого числа есть интересная история — достаточно просто погуглить. Термин был придуман Милтоном Сироттой в 1938 году, когда ему было 9 лет. И хотя это относительно абстрактное число, и его существование объясняется необходимостью технического существования, ему все-таки нашли применение.

Алексис Лемер поставил мировой рекорд, рассчитав корень тринадцати из стозначного числа. Гугол — это стозначное число, число с сотней нулей. Также предполагается, что от одного до полутора гугол лет с момента Большого Взрыва взорвется самая массивная черная дыра. И тогда Вселенная вступит в так называемую «темную эпоху» — конец той научной вселенной, какой мы ее знаем.

8,5 х 10^185

Длина Планка — это очень маленькая длина, примерно 1,616199 x 10-35, или 0,00000000000000000000000000000616199 метра. В дюймовом кубе этих длин примерно с гугол. Длина и объем Планка играют важную роль в отраслях квантовой физике — например, теории струн — поскольку позволяют производить вычисления на самых мельчайших масштабах. Во вселенной примерно 8,5 x 10^185 объемов Планка. Это достаточно большое число, и ему все же нет практического применения, но оно остается достаточно простым в нашем списке.

2^43,112,609 – 1

Третье по величине число в этом списке — это число всех планковых объемов во Вселенной, и в нем 185 цифр. А в этом числе почти 13 миллионов цифр. Чем это число важно? Это самое большое из известных сегодня простых чисел. Его обнаружили в августе 2008 года в ходе Great Internet Messene Prime Search (GIMPS).

Гуголплекс

Вы наверняка слышали это слово, хотя бы в фильме «Назад в будущее», когда доктор Эммет Браун бормотал «она одна на миллион, одна на миллиард, одна на гуголплекс». Что такое гуголплекс? Помните длину гугола? Единица и сто нулей. А гуголплекс — это десять в степени гугол. Это больше, чем число всех частиц в известной нам части вселенной.

Вы можете отметить, что можно возводить десять в степень гуголплекс и будет еще больше, и так далее, и окажетесь совершенно правы.

Числа Скьюза

Число Скьюза — это верхний предел для математической задачи π(x) > Li(x), хоть и просто выглядящей, но крайне сложной на самом деле. По существу, число Скьюза доказывает, что число x существует и нарушает это правило, если предположить, что гипотеза Римана верна, а число x меньше, чем 10^10^10^36, первое число Скьюза. Даже первое число Скьюза больше гуголплекса. Есть также и самое большое число Скьюза: x меньше, чем 10^10^10^963.

Время возвращения Пуанкаре

Это очень сложная вещь, но основная концепция относительно проста: при наличии достаточного времени, все возможно. Теорема Пуанкаре о возвращении предполагает количество времени, которого было бы достаточно для того, чтобы однажды вся Вселенная вернулась в свое нынешнее состояние, вызванное случайными квантовыми флуктуациями. Короче, «история повторится». Предполагается, что это займет 10^10^10^10^10^1,1 лет.

Число Грэма

В 80-х годах это число попало в Книгу рекордов Гиннесса как самое массивное конечное число, когда-либо использованное в математических доказательствах. Оно было выведено Роном Грэмом как верхний предел для проблем теории Рамси о многоцветных гиперкубах. Число настолько большое, что для его записи используется стрелочная нотация Кнута (метод записи больших чисел) и собственное уравнение Грэма. Метод Кнута и принцип работы стрелок сложно объяснить, но вы можете представить себе это так. 3↑3 превращается в 3^3 или 27, 3↑↑3 превращается в 3^3^3 или 7,625,597,484,987. Вы можете добавить еще одну стрелку к 3↑↑↑3 и выйти на 7,5 триллионов уровней. Само по себе это число значительно больше, чем время возвращения Пуанкаре, поскольку вы можете добавить бесконечное число стрелок, и каждая стрелка будет невероятно увеличивать число.

Число Грэма выглядит так: G=f64(4), где f(n)=3↑^n3. Лучший способ его представить — разложить по полочкам. Первый слой — это 3↑↑↑↑3, что уже невероятно много. Следующий слой — это множество стрелок между тройками. Возьмите эти стрелки и поместите между следующими тройками. Это умножается в 64 раза. Даже сам Грэм не знает первое число, но последние десять вот: 2464195387. Вся наблюдаемая вселенная слишком мала, чтобы вместить в себя обыкновенную десятичную запись числа Грэма.

∞. Бесконечность

Это число известно всем и каждому, оно часто используется для преувеличений — как какой-нибудь «многоллион». Однако это число намного сложнее, чем большинство может представить, и если вы могли представить числа, идущие до этого пункта, именно это число очень странное и противоречивое. Согласно правилам бесконечности, есть бесконечное число нечетных и четных чисел в бесконечности, однако только половина от всех чисел может быть четной. Бесконечность плюс один равна бесконечности, бесконечность минус один равна бесконечности, бесконечность плюс бесконечность равна бесконечности, деленная пополам — тоже бесконечность, бесконечность минус бесконечность — никто не знает, бесконечность, деленная на бесконечность, будет, скорее всего, 1.

Ученые полагают, что в известной вселенной около 10^80 субатомных частиц, но это только известная вселенная. Некоторые предполагают, что вселенная бесконечна. Если это так, то математически достоверно, что есть другая Земля где-то там, где каждый атом складывается таким же образом, как и мы, и наша Земля. Шанс того, что копия Земли существует, невероятно мал, но в бесконечной вселенной это не только может произойти, но и бесконечно много раз.

В бесконечность верят не все. Израильский профессор математики Дорон Зильбергер утверждает, что по его мнению, числа не будут продолжаться вечно, и найдется настолько большое число, что когда вы добавите к нему единицу, вы придете к нулю. И хотя это число едва ли когда будет обнаружено и едва ли кто сможет его вообразить, бесконечность является важной частью математической философии.

Источник

Что такое Google BigQuery и почему им стоит пользоваться

Большой объем данных требует широких возможностей для их хранения и обработки. Одним из наиболее полезных и востребованных сервисов в данной сфере является Google BigQuery. Что это за инструмент, какие его возможности и преимущества, с какими платформами его можно интегрировать?

Google BigQuery – что это?

BigQuery – это облачный сервис Google, предназначенный для работы с Big Data, запущен в 2011 году. Он предлагает онлайн-хранилище данных, позволяя надежно хранить и быстро обрабатывать большие массивы информации без необходимости задействовать для этих целей отдельный сервер.

Google BigQuery представляет собой PaaS-сервис («платформа как услуга»), который поддерживает большинство функций СУБД. Он входит в состав Google Cloud Platform, где есть еще несколько десятков приложений для анализа, хранения и вычисления данных.

По сути, BigQuery является облачной БД с неограниченным хранилищем и высокой скоростью обработки больших массивов данных. Он имеет обширный функционал, его пользователи могут оперативно загружать масштабный объем данных, хранить их в виде двумерных таблиц, обращаться к ним используя SQL-запросы, а также сохранять и выгружать их результаты.

Кроме того, возможности Google BigQuery можно расширить при помощи ряда сторонних инструментов. Например, интегрировав его с Google Таблицы, Microsoft Excel, QlikView, BIME Analytics, а также Microsoft Power BI.

Основные функции и возможности Google Big Query

Онлайн-сервис Google BigQuery поддерживает практически все основные функции СУБД, включая структурированное хранение данных, представления и табличные выражения, а также оконные функции. Среди инструментов сервиса имеются функции для работы с датами и строками, а еще для агрегирования данных.

Преимущества Google BigQuery

Облачная база данных Google BigQuery является более удобным и перспективным решением, по сравнению с традиционными СУБД. К числу ее основных преимуществ относятся:

Интеграции Google BigQuery

Онлайн-БД Google BigQuery можно интегрировать с рядом сторонних сервисов для расширения ее функционала. Например, довольно востребованными являются связки BigQuery с различными электронными таблицами, а также платформой Microsoft Power BI. В этом разделе статьи мы кратко расскажем о наиболее популярных из них.

Проще всего интегрировать с BigQuery сервис Google Таблицы – при помощи удобного коннектора от OWOX. Однако в Google Таблицы можно загружать данные только на рабочий лист, а объем одного документа ограничен 2 млн ячеек. Чуть сложнее проходит интеграция BigQuery и Excel, так как их коннектор требует ежемесячно обновлять ключ доступа. Также он позволяет загружать данные только в рабочий лист, а не в модель данных, из-за чего и здесь есть ограничения по объему информации.

Что касается интеграции облачной БД с сервисом QlikView, то для нее нужно создать аккаунт Google Client ID. При этом пользователи получат здесь обширный набор инструментов для визуализации данных. Кроме того, есть возможность для интеграции с Google BigQuery с сервисами BIME и Tableau: каждый из них обеспечивает достойную функциональность и имеет удобный коннектор.

Microsoft Power BI – это мощный профессиональный сервис для визуализации данных, интеграция с которым значительно увеличивает возможности Google BigQuery. Интегрировать их можно при помощи стандартного коннектора «из коробки», однако его возможности весьма ограничены. Лучше использовать для этих целей бесплатный драйвер Simba Drivers, который также подходит для связки BigQuery с электронными таблицами. Кроме того, подключить Microsoft Power BI можно при помощи R-коннектора, предварительно установив среду разработки RStudio.

Выводы

Итак, Google BigQuery – это мощная, удобная, функциональная и доступная по цене облачная база данных. С ее помощью можно загружать и всячески обрабатывать объемные массивы информации без необходимости аренды и администрирования сервера. Она поддерживает большинство ключевых опций современных СУБД, а также легко интегрируется со сторонними платформами для расширения ее функционала.

Источник