Что такое float в питоне
Pythonista. Привет, Python
Предисловие
Доброго времени суток, Хабр. Запускаю короткий курс статей, который охватывает ключевые навыки Python, необходимые для изучения Data Science. Данные статьи подойдут для тех, кто уже имел опыт в программировании и хочет добавить Python в свою копилку навыков.
Привет, Python!
Python был назван в честь популярного британского комедийного телешоу 1970-х «Летающий цирк Монти Пайтона», поскольку автор был поклонником этого телешоу.
Просто ради удовольствия попробуйте прочитать приведенный ниже код и предсказать, что он будет делать при запуске. (Если вы не знаете, это нормально!) Он приурочен скетчу Монти Пайтона про спам.
But I don`t want ANY spam!
Spam Spam Spam Spam
Эта забавная программа демонстрирует многие важные аспекты того, как выглядит код Python и как он работает. Давайте подробнее рассмотрим код.
Обратите внимание: если вы программировали на других языках (например, Java или C ++), вы могли заметить некоторые вещи, которые Python не требует от нас здесь:
• нам не нужно объявлять spam_amount перед присвоением ему значения
Мы будем говорить об «условных выражениях» позже, но, даже если вы никогда раньше не программировали, вы, вероятно, можете догадаться, что тут происходит. Python ценится за его комфортность кода и простоту.
Двоеточие ( : ) в конце строки if указывает, что начинается новый «блок кода». Последующие строки с отступом являются частью этого блока кода. Некоторые другие языки используют < фигурные скобки >для обозначения начала и конца блоков кода. Использование в Python значимых пробелов может удивить программистов, которые привыкли к другим языкам, но на практике это приводит к более согласованному и читаемому коду, чем языки, которые не требуют отступов блоков кода.
Этот фрагмент кода также является нашим первым знакомством со строками в Python:
Строки можно помечать двойными или одинарными кавычками. (Но поскольку эта конкретная строка содержит символ одинарной кавычки, мы можем запутать Python, пытаясь заключить ее в строку, если мы не будем осторожны.)
Числа и арифметика в Python
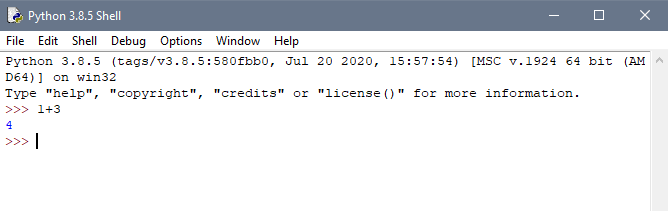
Мы уже видели пример переменной, содержащей число выше:
Числа в Python (FAQ)
Ч исла в Python (как и в других языках программирования) чрезвычайно простое понятие. В Python все переменные представляют собой объекты и размещаются в динамической памяти.
Базовый набор Python содержит следующие типы чисел:
Целые числа (int)
Любое целое число состоит из массива цифр переменной длины, поэтому в Python 3 в переменную типа int может быть записано число неограниченной длины. Единственное ограничение длины — это размер оперативной памяти.
>>> 134523345234252523523478777 ** 2 18096530413013891133013347014216107772438771969415729
Целые числа могут записываться не только как десятичные, но и как двоичные, восьмеричные или шестнадцатеричные. Для этого перед числом нужно написать символы:
Вещественные числа (float)
Числа типа float — неточны (из-за представления чисел с плавающей запятой в компьютере).
>>> 0.3 + 0.3 + 0.3 + 0.1 0.9999999999999999
Информацию о точности и внутреннем представлении float для вашей системы можно получить из sys.float_info
>>> import sys >>> sys.float_info sys.float_info(max=1.7976931348623157e+308, max_exp=1024, max_10_exp=308, min=2.2250738585072014e-308, min_exp=-1021, min_10_exp=-307, dig=15, mant_dig=53, epsilon=2.220446049250313e-16, radix=2, rounds=1)
Если нужна высокая точность обычно используют модули Decimal и Fraction.
Комплексные числа (complex)
Отдельные части комплексного числа доступны через атрибуты real и imag
>>> num = 1.1+2j >>> num.real, num.imag (1.1, 2.0)
Операции с числами
Является ли переменная числом
Любую переменную можно проверить на тип (int, float или complex):
n = 10 >>> if type(n) == int: print(«This is int») This is int
Если вы хотите проверить, находится ли в строке число, воспользуйтесь методом isdigit()
>>> string = «404» >>> string.isdigit() True
Однако стоит помнить, что метод isdigit() не работает для отрицательных чисел и чисел с плавающей точкой.
Также для проверки на число, можно написать собственную функцию:
>>> def isInt(value): try: int(value) return True except ValueError: return False >>> isInt(123) True >>> isInt(«qwerty») False >>> isInt(«123») True >>> isInt(«-123») True >>> isInt(«123.2») False
Арифметические операции
Сравнение чисел
Преобразования
Ввод чисел
Если нужен список чисел, введите несколько чисел через пробел и выполните:
my_list = [int(x) for x in input().split()] print(my_list) > [1, 2, 3]
Вывод чисел
Для вывода числа используйте print() :
На практике возникают ситуации, когда нужно вывести число вместе со строкой (например пояснить, что означает число). Существует несколько вариантов сделать это:
>>> print(«int variable = » + str(1)) int variable = 1 >>> print(«int variable = <>«.format(1)) int variable = 1 >>> print(f’int variable = <1>‘) # f-строки работаюв в Python 3.6+ int variable = 1
Работа с числами в Python
В этом материале рассмотрим работу с числами в Python. Установите последнюю версию этого языка программирования и используйте IDE для работы с кодом, например, Visual Studio Code.
В Python достаточно просто работать с числами, ведь сам язык является простым и одновременно мощным. Он поддерживает всего три числовых типа:
Хотя int и float присутствуют в большинстве других языков программирования, наличие типа комплексных чисел — уникальная особенность Python. Теперь рассмотрим в деталях каждый из типов.
Целые и числа с плавающей точкой в Python
Создание int и float чисел
Для создания целого числа нужно присвоить соответствующее значение переменной. Возьмем в качестве примера следующий код:
Здесь также не стоит использовать кавычки.
В Python также можно создавать крупные числа, но в таком случае нельзя использовать запятые.
Если попытаться запустить этот код, то интерпретатор Python вернет ошибку. Для разделения значений целого числа используется нижнее подчеркивание. Вот пример корректного объявления.
Значение выведем с помощью функции print :
Арифметические операции над целыми и числами с плавающей точкой
Сложение
Результатом будет сумма двух чисел, которая выведется в терминале.
Теперь запустим такой код.
В нем было выполнено сложение целого и числа с плавающей точкой. Можно обратить внимание на то, что результатом также является число с плавающей точкой. Таким образом сложение двух целых чисел дает целое число, но если хотя бы один из операндов является числом с плавающей точкой, то и результат станет такого же типа.
Вычитание
Положительные числа получаются в случае вычитания маленького числа из более крупного. Если же из маленького наоборот вычесть большое, то результатом будет отрицательно число. По аналогии с операцией сложения при вычитании если один из операндов является числом с плавающей точкой, то и весь результат будет такого типа.
Умножение
Если перемножить два целых числа, то результатом будет целое число. Если же использовать число с плавающей точкой, то результатом будет также число с плавающей точкой.
Деление
Деление без остатка
При обычном делении с использованием оператора / результатом будет точное число с плавающей точкой. Но иногда достаточно получить лишь целую часть операции. Для этого есть операции интегрального деления. Стоит рассмотреть ее на примере.
Результатом такой операции становится частное. Остаток же можно получить с помощью модуля, о котором речь пойдет дальше.
Остаток от деления
На этих примерах видно, как это работает.
Возведение в степень
Комплексные числа
Комплексные числа — это числа, которые включают мнимую часть. Python поддерживает их «из коробки». Их можно запросто создавать и использовать. Пример:
Арифметика с типом float в Python: проблемы и ограничения.
К сожалению, большинство десятичных дробей не могут быть представлены точно как двоичные дроби. Следствием этого является то, что, как правило, вводимые десятичные числа с плавающей запятой аппроксимируются только двоичными числами с плавающей запятой, фактически сохраненными в машине.
Многие пользователи не знают о приближении из-за способа отображения значений. Python печатает только десятичное приближение к истинному десятичному значению двоичного приближения, хранящегося на машине. На большинстве машин, если бы Python должен был печатать истинное десятичное значение двоичного приближения, хранящегося для 0.1, он должен был бы отображать
Это больше цифр, чем большинство людей считают полезным, поэтому Python сохраняет количество цифр управляемым, отображая округленное значение вместо
Просто помните, что хотя напечатанный результат выглядит как точное значение 1/10, фактическое сохраненное значение является ближайшей представимой двоичной дробью.
Обратите внимание, что это по своей природе двоичное число с плавающей точкой: это не ошибка в Python и не ошибка в вашем коде. Вы увидите то же самое на всех языках, которые поддерживают арифметику с плавающей запятой.
Для более приятного вывода вы можете использовать форматирование строки для получения ограниченного числа значащих цифр:
Важно понимать, что в действительности это иллюзия: вы просто округляете отображение истинного значения.
Одна иллюзия может породить другую. Например, поскольку 0,1 не является точно 1/10, суммирование трех значений 0,1 может также не дать точно 0,3:
Кроме того, поскольку 0,1 не может приблизиться к точному значению 1/10, а 0,3 не может приблизиться к точному значению 3/10, предварительное округление функцией round() может не помочь:
Двоичная арифметика с плавающей точкой содержит много сюрпризов, подобных этому. Проблема с 0.1 подробно объясняется в разделе «Ошибка представления». Смотрите также «Опасности с плавающей точкой» для более полного описания других распространенных сюрпризов.
Как говорится, «простых ответов нет». Тем не менее, не следует чрезмерно опасаться чисел с плавающей запятой! Ошибки в операциях с плавающей запятой Python наследуются от аппаратного обеспечения чисел с плавающей запятой, и на большинстве машин они имеют порядок не более одной части в 2 ** 53 на операцию. Это более чем достаточно для большинства задач, но вам нужно помнить, что это не десятичная арифметика и что каждая операция с плавающей запятой может подвергаться новой ошибке округления.
Python предоставляет инструменты, которые могут помочь в тех редких случаях, когда вы действительно хотите узнать точное значение числа с плавающей точкой. Метод float.as_integer_ratio() выражает значение типа float в виде дроби:
Поскольку отношение является точным, оно может быть использовано для воссоздания исходного значения без потерь:
Метод float.hex() выражает число с плавающей запятой в шестнадцатеричном формате (основание 16), снова давая точное значение, сохраненное компьютером:
Это точное шестнадцатеричное представление может быть использовано для точного восстановления значения с плавающей точкой:
Поскольку представление является точным, оно полезно для надежного переноса значений между различными версиями Python и обмена данными с другими языками, поддерживающими тот же формат, например Java.
Ошибка представления.
В этом разделе подробно объясняется пример 0.1 и показано, как вы можете выполнить точный анализ подобных случаев самостоятельно. Предполагается базовое знакомство с двоичным представлением чисел с плавающей точкой.
Поскольку остаток больше половины от 10, наилучшее приближение получается округлением вверх:
Таким образом, компьютер никогда не «видит» 1/10: то, что он видит, это точная дробь, указанная выше, наилучшее двоичное приближение 754, которое он может получить:
Это означает, что точное число, хранящееся в компьютере, равно десятичному значению полученному выше. Вместо отображения полного десятичного значения многие языки, включая более старые версии Python округляют результат до 17 значащих цифр:
Модули fractions and decimal упрощают эти вычисления:
15. Арифметика с плавающей запятой: Проблемы и ограничения¶
Числа с плавающей точкой представлены в компьютерных аппаратных средствах как дроби по основанию 2 (двоичная). Например, десятичная дробь
имеет значение 1/10 + 2/100 + 5/1000, и точно также двоичная дробь
имеет значение по 0/2 + 0/4 + 1/8. Эти две дроби имеют одинаковые значения, единственное реальное различие в том, что первое записано по основаниею 10, а второе — по основанию 2.
К сожалению, большинство десятичных дробей не могут быть точно представлено в виде двоичных дробей. Следствием является то, что, вообще говоря, числа с плавающей десятичной точкой, которые вы вводите, только приближенно равны бинарным дробным числам, которые на самом деле сохраняются в машине.
Эту проблему легче понять прежде в случае основания 10. Рассмотрим дробь 1/3. Вы можете приблизить ее дробью по основанию 10:
и так далее. Независимо от того, сколько цифр вы напишите, результат никогда не будет ровно 1/3, но будет все больше лучшим приближением к 1/3.
Таким же образом, независимо от того, сколько цифр по основанию 2 вы напишите, десяичное значение 0.1 не может быть представлено точно в качестве дроби по основанию 2. По основанию 2, 1/10 есть бесконечная периодическая дробь:
Многие пользователи не знают о приближении из-за способа, каким показываются значения. Python печатает только приближение к десятичному значению бинарного приближения, сохраненного машиной. На большинстве машин, если бы Python напечатал настоящее десятичное значение бинарного приближения для 0.1, то он бы показал:
Это кол-во цифр больше того, что большинство людей находят полезным, поэтому Python контролирует кол-во цифр, показывая округленное вместо этого значение:
Просто помните, что хотя даже напечатанное значение и выглядит точным значением 1/10, актуальное хранимое значение является ближайшей представимой бинарной дробью.
Обратите внимание, что в самой природе двоичной плавающей точки: это не ошибка в Python, также как это не ошибка в вашем коде. Вы увидите подобное во всех языках, которые поддерживают арифметику вашего железа (хотя некоторые языки не выводят разницу по умолчанию, или во всех режимах вывода).
Для получения более приятного вывода, вы можете использовать форматирование строк, чтобы вывести ограниченное кол-во значащих цифр:
Важно понимать, что на самом деле это иллюзия: вы просто округляете отображение настоящего машинного числа.
Одна иллюзия может породить другую. Например, так как 0.1 не точно равно 1/10, то суммирование трех значений 0.1 не выдаст ровно 0.3 также:
Также, так как 0.1 не может быть ближе к точному значению 1/10 и 0.3 может быть к точному значению 3/10, то предварительное округление с помощью функции round() не может помочь:
Хотя числа не могут быть приближены к их оригинальным точным значениям, функция round() может быть полезна для пост-округления, так что результаты с неточными значениями становятся сопоставимыми друг с другом:
Двоичная плавающая арифметика хранит много сюрпризов, подобных этому. Проблем с “0.1” объяснена в деталях ниже, в разделе «Ошибка представления». См. Опасности плавающей точки более полный отчет о других распространенных сюрпризах.
Как говорится в конце, «нет простых ответов». Но все равно, не будьте излишне осторожными с плавающей точкой! Ошибки Python-операциями с плавающей точкой переданы по наследству от плавающей точки «железа», и на большинстве машин проявляются на уровне не более чем 1/2**53 на операцию. Это более чем адекватно для большинства задач, но вам должны иметь в виду, что это не десятичная арифметика и что каждая операция с плавающей точкой может допустить новую ошибку округления.
Другая форма точной арифметики поддерживается модулем fractions который реализует арифметику, основанную на рациональных числах (таких, что числа типа 1/3 могут быть представлены точно).
Если вы являетесь серьезным пользователем операций с плавающей точкой, то вам следует посмотреть на пакет Numerical Python и многие другие пакеты для математических и статистических операций, поддерживаемых проектом SciPy.
Python предоставляет инструменты, которые могут помочь в тех редких случаях, когда вы действительно хотите знать точное значение плавающего числа. Метода float.as_integer_ratio() выражает значения float-а как дробь:
Так как дробь точная, это может быть использовано без потери в точности для воссоздания оригинального значения:
Метод float.hex() выражает float в шестнадцатеричном виде (основание 16), снова давая точное значение, хранящееся на вашем компьютере:
Это точное шестнадцатеричное представление может быть использовано для реконструкции значений с плавающей точкой точно:
Так как это представление точно, то оно полезно в качестве надежно портируемых значений между разными версиями Python (независимость от платформы) и обмена данными с другими языками, которые поддерживают тот же формат (такой как Java и C99).
Другой полезный инструмент — функция math.fsum() которая помогает смягчить потерю точности во время суммирования. Она отслеживает «потерянные цифры», когда значения добавляются нарастающим итогом. Это может повлиять на конечную точность, так что ошибки не накапливаются до того момента, где они влияют на окончательный результат:
15.1. Ошибка представления¶
Этот раздел объясняет пример «0.1» в деталях, и показывает, как вы можете выполнить точный анализ подобных случаев сами. Начальное знакомство с бинарным представлением чисел с плавающей точкой предполагается.
Ошибка представления касается того факта, что некоторые (на самом деле большинство) десятичных дробей не могут быть представлены точно в виде двоичных (основание 2) дробей. Это главная причина, почему Python (или C, C++, Java, Fortran, и многи другие) часто не показывают точное десятичное значение, которое вы ожидаете.
Почему так? 1/10 нельзя точно представить в виде двоичной дроби. Большинство машин сегодня (ноябрь 2000) используют арифметику с плавающей точкой IEEE-754, и большинство платформ отображают Python-float-ы на числа IEEE-754 «с двойной точностью». Double-ы 754 содержат 53 бита точности, поэтому на входе компьютер стремится конвертировать 0.1 до ближайшей дроби, которую может, в форме J/2**N, где J есть целое, содержащее ровно 53 бита. Переписывая:
Так как остаток больше, чем половина 10, то лучшее приближение получается при округлении:
Поэтому лучшим возможным округлением к 1/10 в случае двойной точности 754 является:
Поделив и числитель, и знаменатель на 2 редуцирует дробь до:
Заметим, что это фактически немного больше, чем 1/10; в ином случае отношение было бы немного меньше, чем 1/10. Но в любом случае оно не равно точно 1/10!
Поэтому компьютер никогда не видит 1/10: то, что он видит есть точная дробь выше, наилучшее приближение 754, которое он может получить:
Если мы умножим эту дробь на 10**55, то мы можем видеть значение из 55 десятичных цифр:
что означает, что точное число, хранящееся в компьютере равно десятичному значению 0.1000000000000000055511151231257827021181583404541015625. Вместо отображения полного десятичного значения, многие языки (в том числе старые версии Python), округляют результат до 17 значащих цифр:
Модули fractions и decimal делают эти вычисления простыми: