БПФ (Быстрое преобразование Фурье)

Теория БПФ исходит из предположения о периодическом сигнале и для идеального преобразования необходимо выделить точно один или несколько периодов сигнала, что для реального сигнала сделать точно никогда не удается. Это приводит к разрывности исходной функции к искажению (расширению) расчетного частотного спектра.

Оконная функция БПФ используется для подавления краевых эффектов разрывности реальных функций путем введения весовых коэффициентов для выборки данных в окне, обеспечивающих снижение амплитуд краевых точек (старта и стопа) и, в результате, улучшение результатов БПФ.

На скриншотах ниже приведены различные оконные функции, которые используются в цифровых осциллографах Актаком АСК-5302.

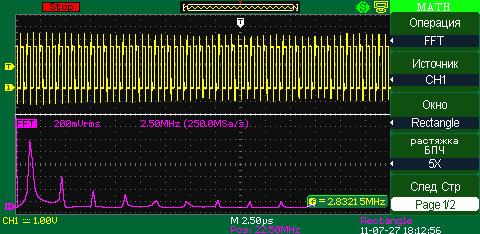
Rectangle (прямоугольник)

Данная оконная функция реализует отличное разрешение по частоте и наихудшее разрешение по амплитуде. Это, по существу, соответствует работе без окна.

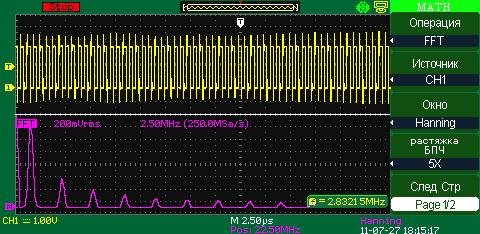
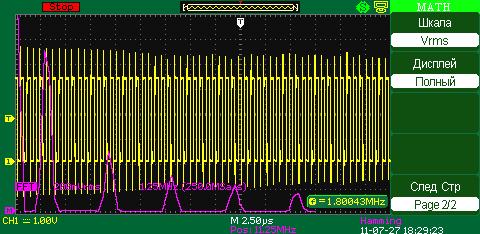
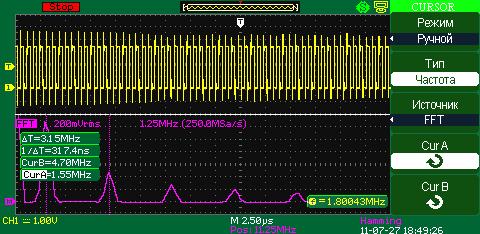
Hanning (окно Хеннинга)

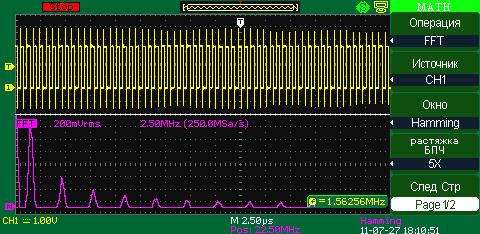
Hamming (окно Хэмминга)

При использовании оконной функции Хэмминга появляется лучшее, чем у Hanning разрешение по частоте

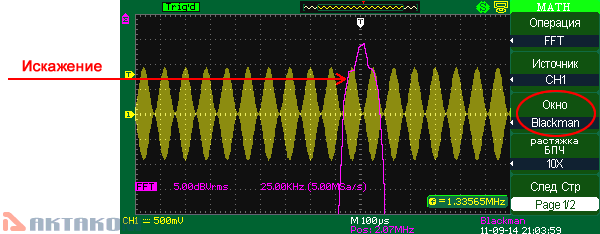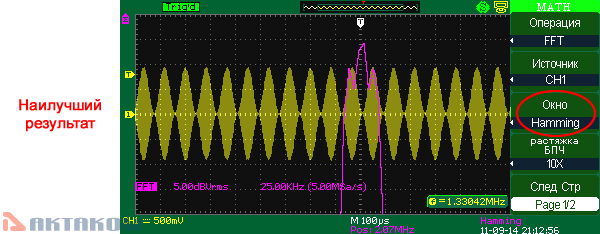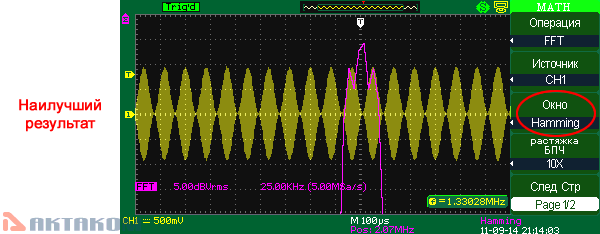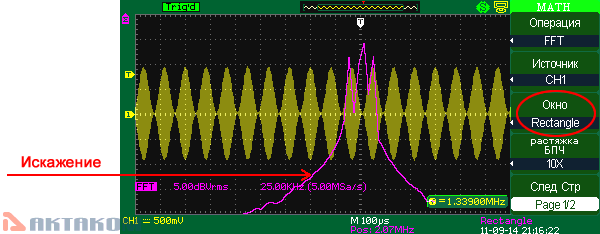
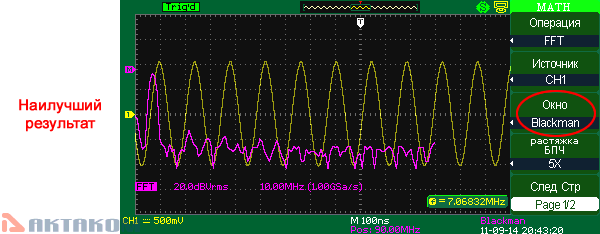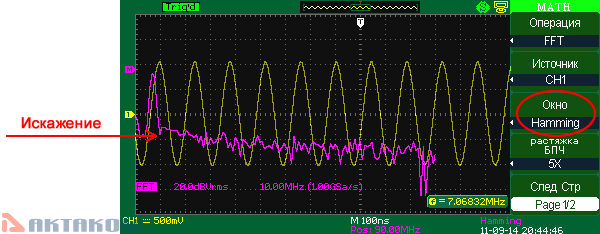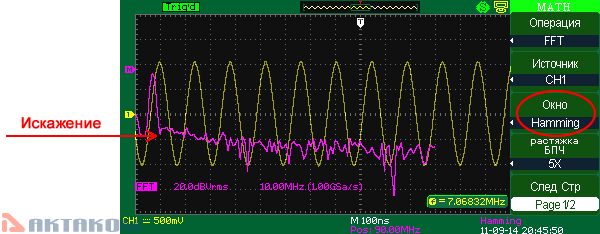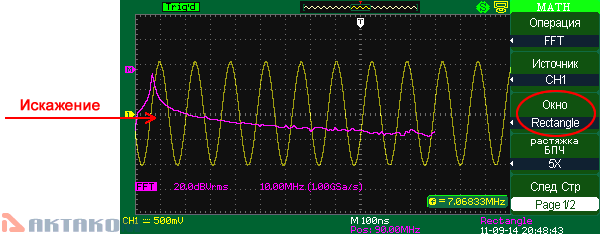
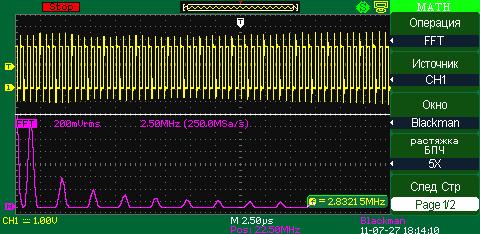
Blackman (окно Блэкмана)

В цифровых осциллографах Актаком для удобства визуализации результата БПФ доступны ряд дополнительных средств. Среди них следует отметить:

В цифровых осциллографах режим БПФ может применяться в следующих случаях:

Источник

Преобразование Фурье в действии: точное определение частоты сигнала и выделение нот

Начнём с пианино. Очень упрощёно этот музыкальный инструмент представляет собой набор белых и чёрных клавиш, при нажатии на каждую из которых извлекается определённый звук заранее заданной частоты от низкого до высокого. Конечно, каждый клавишный инструмент имеет свою уникальную тембральную окраску звучания, благодаря которой мы можем отличить, например, аккордеон от фортепиано, но если грубо обобщить, то каждая клавиша представляет собой просто генератор синусоидальных акустических волн определённой частоты.

Когда музыкант играет композицию, то он поочерёдно или одновременно зажимает и отпускает клавиши, в результате чего несколько синусоидальных сигналов накладываются друг на друга образуя рисунок. Именно этот рисунок воспринимается нами как мелодия, благодаря чему мы без труда узнаём одно произведение, исполняемое на различных инструментах в разных жанрах или даже непрофессионально напеваемое человеком.

Наглядная иллюстрация нотного рисунка

Определение частоты (режим гитарного тюнера)

Обратная задача состоит в том, чтобы разобрать звучащую музыкальную композицию на ноты. То есть разложить суммарный акустический сигнал, улавливаемый ухом, на исходные синусоиды. По сути, этот процесс и представляет собой прямое преобразование Фурье. А нажатие на клавиши и извлечение звука есть процесс обратного преобразования Фурье.

Математически в первом случае происходит разложение сложной периодической (на некотором временном интервале) функции в ряд более элементарных ортогональных функций (синусоид и косинусоид). А во втором их обратное суммирование, то есть синтез сложного сигнала.

Ортогональность, в некотором роде, обозначает несмешиваемость функций. Например, если мы возьмём несколько кусочков цветного пластилина и склеим их, то потом всё же сможем разобрать, какие цвета были изначально, но если хорошенько перемешаем несколько баночек гуашевых красок, то точно восстановить исходные цвета без дополнительной информации уже будет невозможно.

(!) Важно понимать, когда мы берёмся анализировать реальный сигнал с помощью преобразования Фурье, мы идеализируем ситуацию и исходим из предположения, что он периодический на текущем временном интервале и состоит из элементарных синусоид. Зачастую это именно так, поскольку акустические сигналы, как правило, имеют гармоническую природу, но вообще возможны и более сложные случаи. Любые наши допущения о природе сигнала обычно ведут к частичным искажениям и погрешностям, но без этого выделить полезную информацию из него крайне сложно.

Теперь опишем весь процесс анализа более подробно:

1. Всё начинается с того, что звуковые волны колеблют мембрану микрофона, который преобразует их в аналоговые колебания электрического тока.

2. Затем происходит дискретизация аналогового электрического сигнала в цифровую форму. На этом моменте стоит остановиться подробно.

Поскольку аналоговый сигнал математически состоит из бесконечного непрерывного во времени множества точек-значений амплитуды, в процессе измерения мы можем выделить из него лишь конечный ряд значений в дискретные моменты времени, то есть, по сути, выполнить квантование по времени…

Как правило, значения-отсчёты берутся через небольшие равные временные промежутки, то есть с определённой частотой, например, 16000 или 22000 Гц. Однако в общем случае дискретные отсчёты могут идти и неравномерно, но это усложняет математический аппарат анализа, поэтому на практике обычно не применяется.

Существует важная теорема Котельникова-Найквиста-Шеннона, которая гласит, что аналоговый периодический сигнал, имеющий конечный (ограниченный по ширине) спектр, может быть однозначно восстановлен без искажений и потерь по своим отсчётам, взятым с частотой, большей или равной удвоенной верхней частоте спектра (называемой частотой дискретизации или Найквиста).

Для этого восстановления необходимо применить специальные интерполирующие функции, но проблема в том, что при использовании данных функций вычисления нужно выполнять на бесконечном временном интервале, что на практике невозможно. Поэтому в реальной жизни нельзя сколь угодно повысить частоту дискретизации искусственным образом без искажений даже если изначально она удовлетворяет теореме Котельникова-Найквиста-Шеннона. Для этой операции применяются фильтры Фарроу.

Также дискретизация происходит не только по времени, но и по уровню значений амплитуды, поскольку компьютер способен манипулировать лишь ограниченным множеством чисел. Это также вносит небольшие погрешности.

3. На следующем этапе происходит само дискретное прямое преобразование Фурье.

Мы выделяем короткий кадр (интервал) композиции, состоящий из дискретных отсчётов, который условно считаем периодическим и применяем к нему преобразование Фурье. В результате преобразования получаем массив комплексных чисел, содержащий информацию об амплитудном и фазовом спектрах анализируемого кадра. Причём спектры также являются дискретными с шагом равным (частота дискретизации)/(количество отсчётов). То есть чем больше мы берём отсчётов, тем более точное разрешение получаем по частоте. Однако при постоянной частоте дискретизации увеличивая число отсчётов, мы увеличиваем анализируемый временной интервал, а поскольку в реальных музыкальных произведениях ноты имеют различную длительность звучания и могут быстро сменять друг друга, происходит их наложение, поэтому амплитуда длительных нот «затмевает» собой амплитуду коротких. С другой стороны для гитарных тюнеров такой способ увеличения разрешения по частоте подходит хорошо, поскольку нота, как правило, звучит долго и одна.

Существует также довольно простой трюк для увеличения разрешения по частоте — нужно исходный дискретный сигнал заполнить нулями между отсчётами. Однако в результате такого заполнения сильно искажается фазовый спектр, но зато увеличивается разрешение амплитудного. Также возможно применение фильтров Фарроу и искусственное увеличение частоты дискретизации, однако и оно вносит искажения в спектры.

Длительность кадра обычно составляет приблизительно от 30 мс до 1 с. Чем он короче, тем лучшее разрешение мы получаем по времени, но худшее по частоте, чем сэмпл длиннее, тем лучшее по частоте, но худшее по времени. Это очень напоминает принцип неопределённости Гейзенберга из квантовой механики..и не с проста, как гласит Википедия, соотношение неопределенностей в квантовой механике в математическом смысле есть прямое следствие свойств преобразования Фурье…

Интересно и то, что в результате анализа сэмпла одиночного синусоидального сигнала амплитудный спектр очень напоминает дифракционную картинку…

Синусоидальный сигнал, ограниченный прямоугольным окном, и его «дифракция»

Дифракция световых волн

На практике это нежелательный эффект, затрудняющий анализ сигналов, поэтому его стараются понизить путём применения оконных функций. Таких функций придумано немало, ниже представлены реализации некоторых из них, а также сравнительное влияние на спектр одиночного синусоидального сигнала.

Применяется оконная функция ко входному кадру очень просто:

Что касается компьютеров, в своё время был разработан алгоритм быстрого преобразования Фурье, который минимизирует число математических операций, необходимых для его вычисления. Единственное требование алгоритма состоит в том, чтобы число отсчётов было кратно степени двойки (256, 512, 1024 и так далее).

Ниже его классическая рекурсивная реализация на языке C#.

Существует две разновидности алгоритма БПФ — с прореживанием по времени и по частоте, но оба дают идентичный результат. Функции принимают массив комплексных чисел, заполненный реальными значениями амплитуд сигнала во временной области, а после своего выполнения возвращают массив комплексных чисел, содержащий информацию об амплитудном и фазовом спектрах. Стоит помнить, что реальная и мнимая части комплексного числа — это далеко не то же самое, что его амплитуда и фаза!

magnitude = Math.Sqrt(x.Real*x.Real + x.Imaginary*x.Imaginary)
phase = Math.Atan2(x.Imaginary, x.Real)

Результирующий массив комплексных чисел заполнен полезной информацией ровно на половину, другая половина является лишь зеркальным отражением первой и спокойно может быть исключена из рассмотрения. Если вдуматься, то этот момент хорошо иллюстрирует теорему Котельникова-Найквиста-Шеннона, о том, что частота дискретизации должна быть не меньше максимальной удвоенной частоты сигнала…

Также существует разновидность алгоритма БПФ без рекурсии по Кули-Тьюки, которая часто применяется на практике, но она чуть более сложна для восприятия.

Сразу после вычисления преобразования Фурье удобно нормализовать амплитудный спектр:

Это приведёт к тому, что величина значений амплитуды получится одного порядка не зависимо от размеров сэмпла.

Вычислив амплитудный и частотный спектры, легко производить обработку сигнала, например, применять частотную фильтрацию или производить сжатие. По сути, таким образом можно сделать эквалайзер: выполнив прямое преобразование Фурье, легко увеличить или уменьшить амплитуду определённой области частот, после чего выполнить обратное преобразование Фурье (хотя работа настоящих эквалайзеров обычно основана на другом принципе — фазовом сдвиге сигнала). Да и сжать сигнал очень просто — нужно всего лишь сделать словарь, где ключом является частота, а значением соответствующее комплексное число. В словарь нужно занести лишь те частоты, амплитуда сигнала на которых превышает какой-то минимальный порог. Информация о «тихих» частотах, не слышимых ухом, будет потеряна, но получится ощутимое сжатие при сохранении приемлемого качества звучания. Отчасти этот принцип лежит в основе многих кодеков.

4. Точное определение частоты

Дискретное преобразование Фурье даёт нам дискретный спектр, где каждое значение амплитуды отстоит от соседних на равные промежутки по частоте. И если частота в сигнале кратна шагу равному (частота дискретизации)/(количество отсчётов), то мы получим выраженный остроконечный пик, но если частота сигнала лежит где-то между границами шага ближе к середине у нас выйдет пик со «срезанной» вершиной и нам будет затруднительно сказать, что же там за частота. Очень может быть что в сигнале присутствуют две частоты лежащие рядом друг с другом. В этом и заключается ограничение разрешения по частоте. Так же как на фотоснимке с низким разрешением мелкие предметы склеиваются и становятся неразличимы, так же и тонкие детали спектра могут теряться.

Но частоты музыкальных нот лежат далеко не на сетке шагов преобразования Фурье, а для повседневных задач настройки музыкальных инструментов и распознавания нот необходимо знать именно точную частоту. Более того, на низких октавах при разрешении от 1024 отсчётов и ниже сетка частот Фурье становится настолько редкой, что попросту на одном шаге начинают умещаться несколько нот и определить какая же на самом деле из них играет становится фактически невозможно.

Чтобы как-то обойти это ограничение иногда применяют аппроксимирующие функции, например, параболические.
www.ingelec.uns.edu.ar/pds2803/Materiales/Articulos/AnalisisFrecuencial/04205098.pdf
mgasior.web.cern.ch/mgasior/pap/biw2004_poster.pdf
Но всё это искусственные меры, которые улучшая одни показатели могут давать искажения в других.

Существует ли более естественный путь для точного определения частоты?
Да, и скрыт он как раз-таки в использовании фазового спектра сигнала, которым часто пренебрегают.
Данный метод уточнения частоты сигнала, основан на вычислении задержки фаз у спектров двух кадров, наложенных друг на друга, но немного сдвинутых во времени.

На C# реализация метода выглядит довольно просто:

Применение также несложное:

Обычно исходные кадры сдвинуты на 1/16 или 1/32 своей длины, то есть ShiftsPerFrame равно 16 или 32.

В результате мы получим словарь частота-амплитуда, где значения частот будут довольно близки к реальным. Однако «срезанные пики» всё ещё будут наблюдаться, хоть и менее выражено. Чтобы устранить этот недостаток, можно просто «дорисовать» их.

Нотный анализ музыкальных произведений открывает ряд интересных возможностей. Ведь имея в наличии готовый нотный рисунок, можно осуществлять поиск других музыкальных композиций со схожим рисунком.

Например, одно и то же произведение может быть исполнено на другом инструменте, в различной манере, с другим тембром, либо транспонировано по октавам, однако нотный рисунок останется похожим, что позволит найти различные варианты исполнения одного и того же произведения. Это очень напоминает игру «угадай мелодию».

В некоторых случаях подобный анализ поможет выявить плагиат в музыкальных произведениях. Также по нотному рисунку, теоретически, можно искать произведения определённого настроения или жанра, что поднимает поиск на новый уровень.

В этой статье изложены основные принципы точного определения частот акустических сигналов и выделения нот. А также показана некоторая тонкая интуитивная связь дискретного преобразования Фурье с квантовой физикой, что подталкивает на размышления о единой картине мира.

Источник

Что такое fft в осциллографе

В статье рассмотрены основы теоретического и практического применения быстрого преобразования Фурье в цифровых запоминающих осциллографах. Приведены экспериментальные данные по оценке метрологических характеристик осциллографа в режиме преобразования Фурье.

Большинство современных цифровых запоминающих осциллографов (ЦЗО) оснащены алгоритмом быстрого преобразования Фурье (БПФ) для проведения анализа сигнала не только во временной, но и в частотной области. Этот алгоритм особенно полезен для пользователей, которым необходимо проводить спектральный анализ, но у которых отсутствуют специализированные приборы типа анализаторов спектра (АС). При этом пользователям надо четко представлять, что ЦЗО является, прежде всего, осциллографом, а не средством измерения частотного спектра, хотя у него и есть такая возможность. Поэтому метрологические характеристики ЦЗО в режиме БПФ не нормируются. Несмотря на это и тот факт, что АС имеют лучший динамический диапазон и меньшие искажения, с помощью БПФ ЦЗО можно получить полезные результаты. Однако, в отличие от АС, получение такого результата во многом будет зависеть от того, насколько хорошо пользователь осведомлен о работе алгоритма БПФ и его режимах, о виде исследуемого сигнала, а также об ограничениях, накладываемых аппаратной и программной частями ЦЗО. Далее в статье рассмотрены теоретические и практические основы применения БПФ в ЦЗО [1,2].

Рассмотрим некоторые свойства дискретного преобразования Фурье (ДПФ), чтобы определить ограничения в использовании БПФ для спектрального анализа. ДПФ представляет собой дискретные отсчеты непрерывного преобразования Фурье (разложение в ряд Фурье). Поскольку разложение в ряд Фурье подразумевает наличие бесконечной во времени функции данных, чего на практике не существует, для ДПФ бесконечная последовательность формируется репликацией данной конечной последовательности. Если начальные и конечные точки последовательности не согласованы, то полученная функция бесконечной последовательности будет иметь разрывы первого рода. Такой разрыв во временной области приводит к эффекту спектрального пролезания в частотной области, проявляющемуся в виде растягивания четких спектральных линий в широкую полосу. Данный эффект может привести к потере полезного сигнала, который будет скрыт широкой спектральной полосой другого сигнала.

БПФ является алгоритмом для вычисления ДПФ, который позволяет сократить количество математических операций и соответственно время вычисления по сравнению с непосредственным расчетом ДПФ. Существует несколько подвидов алгоритма БПФ. Не останавливаясь на их подробном описании, выделим важные для практического применения особенности:

В ЦЗО алгоритм БПФ применяется только для тех точек, отображающих входной сигнал, которые находятся на экране осциллографа. Количество захваченных точек может не быть точно равно 2N, поэтому для работы алгоритма БПФ последовательность либо укорачивается до нужного числа точек, либо в конец последовательности добавляются нули для достижения нужного числа точек. Как следует из формулы (1), увеличение точек для БПФ увеличивает разрешение по частоте. Но добавление нулей хотя и не изменяет форму сигнала во временной области, может вызвать эффект искажения его спектра. Для предотвращения этого эффекта, а также спектрального пролезания применяют так называемые функции окна.

Примерным объяснением функции окна может являться аналогия с пропускающим фильтром АС. Исходя из этого, функция окна будет выделять спектральные линии из шумов и уменьшать ширину спектральных линий. Однако надо иметь в виду, что применение окон вносит изменения в полученный набор точек для БПФ и может привести к искажению спектра сигнала. Например, такие искажения могут появиться, если сигнал расположен не в центре экрана ЦЗО [3].

Вид функции окна определяет получаемые характеристики эквивалентного фильтра: ширину полосы пропускания, неравномерность амплитуды в полосе пропускания и уровень подавления помех относительно полезного сигнала. Поскольку идеальных фильтров не бывает, в БПФ используются различные виды окон. Рассмотрим две основные функции окна: прямоугольного (не вносит никаких изменений в сигнал) и плоского окна. Прямоугольное окно обеспечивает самую узкую полосу пропускания, равную разрешению по частоте (1), но характеризуется уровнем подавления помех относительно несущей около 13 дБ и может привести к ошибке в измерении амплитуды сигнала из-за применения окна до 4 дБ. Плоское окно имеет следующие характеристики: полоса пропускания ±4B?F (таким образом, для получения такого же эффективного разрешения по частоте, как у прямоугольного окна, для БПФ требуется в 8 раз больше точек), уровень подавления помех относительно несущей более 70 дБ и погрешность измерения амплитуды из-за применения окна не более 0,1 дБ. Соответственно, первое окно можно применять для частотных измерений, а второе — для амплитудных.

Динамический диапазон БПФ ЦЗО, кроме применяемых функций окна, ограничен разрешением аналогово-цифрового преобразователя (АЦП) и вносимыми им искажениями, внутренними шумами прибора, а также неравномерностью амплитудо-частотной характеристики осциллографа. Обычно динамический диапазон для БПФ ЦЗО с 8-разрядными АЦП составляет не менее 50 дБ и может быть увеличен еще на 20 дБ при помощи усреднения сигнала во временной области.

Все изложенное относится к ЦЗО, работающим в режиме реального времени. Для исследования спектра периодических сигналов может применяться режим эквивалентной дискретизации. Но его применение не улучшает работу БПФ, так как по (1) увеличение частоты дискретизации снижает разрешение по частоте.

Теперь рассмотрим результаты практического использования БПФ и оценим полученные при этом погрешности на примере трех осциллографов: ЦЗО среднего уровня с малой памятью (TDS3032: полоса пропускания 300 МГц, память 10 КБ, частота дискретизации выбирается автоматически в зависимости от установленного коэффициента развертки, F_s,max=5 ГГц) и с большой памятью (WS454: полоса пропускания 500 МГц, память 2 МБ, частота дискретизации выбирается автоматически в зависимости от установленного коэффициента развертки, F_s,max=2 ГГц), а также ЦЗО класса «high-end» (WavePro7100: полоса пропускания 1 ГГц, память 48 МБ, частота дискретизации может устанавливаться пользователем, F_s,max=20 ГГц). Все измерения проводились с использованием средств измерений по схеме, приведенной на рис. 1.

Подадим на TDS3032 синусоидальный сигнал с частотой 70 МГц; после запуска БПФ отображаются спектральные линии, соответствующие несущей и гармоникам (рис. 2). Курсорные измерения показывают частоту несущей и ее уровень. Однако, уже при подаче сложного сигнала, например амплитудно-модулированного (АМ) синусоидального сигнала с несущей частотой 100 МГц, частотой модуляции синусоидальным сигналом 1 кГц и коэффициентом модуляции 70%, на спектрограмме БПФ отсутствует характерный спектр АМ-сигнала (рис. 3). Данный факт легко объясняется формулой (1), при малом объеме памяти 10 КБ и частоте дискретизации 5 ГГц разрешение по частоте БПФ значительно превышает 1 кГц, что не позволяет различить на фоне спектральной линии несущей частоту модулирующего колебания. Таким образом, БПФ в осциллографах начального, а иногда и среднего уровня с малой памятью не позволяет проводить какие-либо достоверные измерения и является программным дополнением, годящимся лишь для оценочного наблюдения спектра простейших сигналов.

Проведем аналогичный опыт с ЦЗО WS454. На экране прибора присутствует информация об установленной частоте дискретизации и количестве точек на экране. Изменяя коэффициент развертки, задействуем максимальную память осциллографа при минимально возможной для данного эксперимента частоте дискретизации. В случае с синусоидальным сигналом частотой 70 МГц частота дискретизации должна быть более чем в два раза больше частоты третьей гармоники сигнала (210 МГц), то есть больше чем 420 МГц. В случае АМ-сигнала с частотой 100 МГц частота дискретизации должна быть больше 200 МГц. Поскольку непосредственное управление частотой дискретизации в WS454 отсутствует, требования по памяти и Fs выполняются при установке коэффициента развертки в положение 500 мкс/дел (тогда на экране отображается 2 МБ точек с F_s = 500 МГц). При соседних коэффициентах развертки Fs составляет 200 МГц или 1 ГГц, что либо меньше требуемого, либо много больше требуемого. Существенно увеличивать F_s не нужно, ибо это приведет к ухудшению разрешения по частоте БПФ. Полученные после запуска БПФ для случаев синусоидального и АМ-сигналов спектрограммы приведены на рис. 4 и 5. Для синусоидального сигнала выбрано плоское окно, на спектрограмме видны несущая и гармоники сигнала, можно провести частотные и амплитудные измерения. Для АМ-сигнала выбрано прямоугольное окно, обеспечивающее максимальное разрешение по частоте. Однако на спектрограмме видно, что хотя спектральная составляющая модулирующего колебания 1 кГц различима на фоне несущей, для проведения измерений этого не достаточно: амплитудные измерения нельзя провести из-за формы окна, а частотные — по причине малого разрешения по частоте БПФ (±250 Гц). Таким образом, даже относительно большой объем памяти в ЦЗО не всегда позволяет провести эффективные измерения в режиме БПФ для сложных сигналов.

Теперь подадим такие же сигналы на WavePro7100. Пусть подается синусоидальный сигнал с частотой 70 МГц и требуется определить его частоту, уровень и гармонические искажения. Для этого установим на ЦЗО частоту дискретизации 500 МГц. Чтобы избежать дополнительной программной ошибки в измерении амплитуды, выберем плоское окно, а для получения максимального количества точек для БПФ установим режим дополнения последовательности нулями до 2N и максимальный объем памяти (в данном случае 16 МБ). Поскольку все точки БПФ должны быть на экране ЦЗО, необходимо установить коэффициент развертки в положение 5 мс/дел. После однократного запуска ЦЗО включим обработку БПФ. При установке центральной частоты спектрограммы 70 МГц и полосы обзора 1 кГц/дел на экране будет отображаться первая гармоника сигнала (рис. 6), изменяя центральную частоту и полосу обзора можно наблюдать другие гармоники.

Теперь подадим на ЦЗО АМ-сигнал и определим его параметры: частоту несущего и модулирующего колебаний, коэффициент гармоник огибающей модулирующего сигнала и коэффициент амплитудной модуляции (Кам). Исходя из параметров сигнала и требуемых задач, установим частоту дискретизации 250 МГц, остальные настройки остаются такими же, как и в предыдущем измерении. Для уменьшения случайной погрешности измерения проводились не только в курсорном режиме, но и в автоматическом — с использованием разработанного для вычисления Кам скрипта VisualBasic, который подключается к программному обеспечению ЦЗО. Результаты измерений по спектрограмме (рис. 7) и коэффициента АМ по осциллограмме (рис. 8).

При правильных настройках БПФ в ЦЗО класса «high-end» с большой памятью можно получать результаты измерений, не уступающие значительно по точности измерениям на специализированных приборах: анализаторах спектра, частотомерах, измерителях нелинейных искажений и амплитудной модуляции. С помощью несложных расчетов подтвердим пригодность ЦЗО класса «high-end» с большим объемом памяти для осуществления алгоритма БПФ с приемлемым результатом для любых входных сигналов сложного вида. Современные ЦЗО имеют полосу пропускания до 6-8 ГГц и частоту дискретизации до 20 ГГц, при этом их алгоритмы БПФ способны обрабатывать до 24 МБ данных (скорость обработки такого массива данных составляет до 1 минуты). Таким образом, по формуле (1) можно обеспечить разрешение по частоте БПФ порядка 1 кГц. Данное значение является допустимым при спектральном анализе по сравнению с погрешностью по частоте ЦЗО для сигналов с частотами 6-8 ГГц, абсолютное значение которой составляет до 8 кГц. Для сигналов более низких частот разрешение по частоте БПФ в ЦЗО класса «high-end» может быть увеличено благодаря возможности независимой регулировки объема памяти и частоты дискретизации.

Выводы

ЦЗО не имеют нормируемых метрологических характеристик в режиме БПФ и не могут служить полной заменой специализированным приборам.

Эффективные результаты после применения БПФ можно получить только в случае понимания особенностей построения, реализации и ограничений данного алгоритма в ЦЗО, а также знания некоторой априорной информации о сигнале.

БПФ в ЦЗО с малой памятью и отсутствием регулировки частоты дискретизации пользователем позволяет получать только оценочные спектрограммы простейших сигналов и не может использоваться для анализа сложных сигналов.

ЦЗО класса «high-end» с объемом памяти от 8 МБ до 24 МБ позволяют при соблюдении всех требований получать результаты спектральных измерений сложных сигналов при помощи БПФ во всей полосе пропускания с точностью на уровне специализированных приборов. Таким образом, БПФ расширяет возможности данных осциллографов по анализу входных сигналов.

Источник