Что такое erfi в математике
Документация
Мнимая функция ошибок
Синтаксис
Описание
Примеры
Мнимая функция ошибок для с плавающей точкой и символьных чисел
В зависимости от его аргументов, erfi может возвратить или точные символьные результаты с плавающей точкой.
Вычислите мнимую функцию ошибок для этих чисел. Поскольку эти числа не являются символьными объектами, вы получаете результаты с плавающей точкой.
Вычислите мнимую функцию ошибок для тех же чисел, преобразованных в символьные объекты. Для большинства символьных (точных) чисел, erfi отвечает на неразрешенные символьные звонки.
Использование vpa аппроксимировать этот результат 10-разрядной точностью:
Мнимая функция ошибок для переменных и выражений
Мнимая функция ошибок для векторов и матриц
Если входной параметр является вектором или матрицей, erfi возвращает мнимую функцию ошибок для каждого элемента того вектора или матрицы.
Вычислите мнимую функцию ошибок для элементов матричного M и векторный V :
Специальные значения мнимой функции ошибок
Вычислите мнимую функцию ошибок для комплексных бесконечностей. Используйте sym преобразовывать комплексные бесконечности в символьные объекты:
Обработка выражений, которые содержат мнимую функцию ошибок
Вычислите первые и вторые производные мнимой функции ошибок:
Вычислите интегралы этих выражений:
Постройте мнимую функцию ошибок
Постройте мнимую функцию ошибок на интервале от-2 до 2.
Входные параметры
x входной параметр
число с плавающей запятой | символьное число | символьная переменная | символьное выражение | символьная функция | символьный вектор | символьная матрица
Введите в виде с плавающей точкой или символьного числа, переменной, выражения, функции, вектора или матрицы.
Больше о
Мнимая функция ошибок
Мнимая функция ошибок задана как:
e r f i ( x ) = − i e r f ( i x ) = 2 π ∫ 0 x e t 2 d t
Советы
erfi возвращает специальные значения для этих параметров:
Смотрите также
Открытый пример
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
Документация Symbolic Math Toolbox
Поддержка
© 1994-2021 The MathWorks, Inc.
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.
и функция мнимой ошибки ( erfi ), определяемая как
СОДЕРЖАНИЕ
Название «функция ошибок» и ее сокращение erf были предложены Дж. В. Л. Глейшером в 1871 г. в связи с его связью с «теорией вероятности и, в частности, теорией ошибок ». Дополнение к функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона удобства» ошибок, плотность которых определяется как
( нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p и q, как:
Приложения
Функция ошибок и ее приближения могут использоваться для оценки результатов, которые имеют высокую или низкую вероятность. Дана случайная величина X
Характеристики
Серия Тейлора
Для итеративного расчета вышеуказанного ряда может быть полезна следующая альтернативная формулировка:
Функция мнимой ошибки имеет очень похожий ряд Маклорена, а именно:
Производная и интеграл
Производная функции ошибок сразу следует из ее определения:
Отсюда немедленно вычисляется производная мнимой функции ошибок:
Первообразной функции мнимой ошибки, которую также можно получить интегрированием по частям, является
Производные высшего порядка даются формулами
Серия Bürmann
Разложение, которое сходится быстрее для всех действительных значений x, чем разложение Тейлора, получается с помощью теоремы Ганса Генриха Бюрмана :
Обратные функции
Итак, у нас есть расширение в ряд (общие множители из числителей и знаменателей удалены):
Обратная дополнительная функция ошибок определяются как
где c k определено, как указано выше.
Асимптотическое разложение
Полезное асимптотическое разложение дополнительной функции ошибок (и, следовательно, также функции ошибок) для больших действительных x :
Действительно, точное значение остатка равно
что легко следует по индукции, записывая
и интеграция по частям.
Для достаточно больших значений x необходимы только первые несколько членов этого асимптотического разложения, чтобы получить хорошее приближение erfc x (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Непрерывное расширение фракции
Цепная дробь расширение дополнительной функции ошибок является:
Интеграл функции ошибок с функцией плотности Гаусса
которая, по-видимому, связана с Нг и Геллером, формула 13 в разделе 4.3 с заменой переменных.
Факторный ряд
Численные приближения
Приближение с элементарными функциями
(максимальная ошибка: 2,5 × 10 −5 )
Это приближение можно инвертировать, чтобы получить приближение для обратной функции ошибок:
Таблица значений
Связанные функции
Дополнительная функция ошибок
Функция мнимой ошибки
Несмотря на название «мнимая функция ошибок», erfi x реально, когда x реально.
Кумулятивная функция распределения
или переставил для erf и erfc :
Стандартный нормальный cdf чаще используется в вероятностях и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера и также может быть выражена как конфлюэнтная гипергеометрическая функция ( функция Куммера):
Обобщенные функции ошибок
Некоторые авторы обсуждают более общие функции:
Эти обобщенные функции могут быть эквивалентно выражены для x > 0 с использованием гамма-функции и неполной гамма-функции :
Следовательно, мы можем определить функцию ошибок в терминах неполной гамма-функции:
Итерированные интегралы дополнительной функции ошибок
Повторные интегралы дополнительной функции ошибок определяются как
Общая рекуррентная формула
У них есть степенной ряд
откуда следуют свойства симметрии
Функция ошибки
и функция мнимой ошибки ( erfi ), определяемая как
СОДЕРЖАНИЕ
Имя [ редактировать ]
Название «функция ошибок» и его сокращение erf были предложены Дж. В. Л. Глейшером в 1871 г. в связи с его связью с «теорией вероятности, и особенно теорией ошибок ». [2] Дополнение к функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. [3] Для «закона легкости» ошибок, плотность которых определяется как
Приложения [ править ]
Pr [ X ≤ L ] = 1 2 + 1 2 erf ( L − μ 2 σ ) ≈ A exp ( − B ( L − μ σ ) 2 ) <\displaystyle \Pr[X\leq L]=<\frac <1><2>>+<\frac <1><2>>\operatorname
Pr [ X ≤ L ] ≤ A exp ( − B ln k ) = A k B <\displaystyle \Pr[X\leq L]\leq A\exp(-B\ln
Свойства [ править ]
Для любого комплексного числа z :
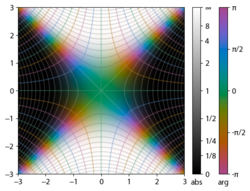
Подынтегральное выражение f = exp (- z 2 ) и f = erf ( z ) показано на комплексной плоскости z на рисунках 2 и 3. Уровень Im ( f ) = 0 показан жирной зеленой линией. Отрицательные целые значения Im ( f ) показаны толстыми красными линиями. Положительные целые значения Im ( f ) показаны толстыми синими линиями. Промежуточные уровни Im ( f ) = constant показаны тонкими зелеными линиями. Промежуточные уровни Re ( f ) = constant показаны тонкими красными линиями для отрицательных значений и тонкими синими линиями для положительных значений.
Функция ошибок при + ∞ равна 1 (см. Интеграл Гаусса ). На действительной оси erf ( z ) стремится к единице при z → + ∞ и к −1 при z → −∞. На мнимой оси он стремится к ± i ∞.
Серия Тейлор [ править ]
Для итеративного расчета вышеуказанного ряда может быть полезна следующая альтернативная формулировка:
Функция мнимой ошибки имеет очень похожий ряд Маклорена, а именно:
Производные и интегральные [ править ]
Производная функции ошибок сразу следует из ее определения:
Отсюда немедленно вычисляется производная мнимой функции ошибок:
Первообразной функции мнимой ошибки, которую также можно получить интегрированием по частям, является
Производные высшего порядка даются формулами
Серия Bürmann [ править ]
Обратные функции [ править ]
Функция обратной ошибки обычно определяется с помощью области (-1,1), и она ограничена этой областью во многих системах компьютерной алгебры. Однако его можно распространить на диск | z | комплексной плоскости, используя ряд Маклорена
Итак, у нас есть расширение в ряд (общие множители из числителей и знаменателей удалены):
Обратная дополнительная функция ошибок определяются как
где c k определено, как указано выше.
Асимптотическое разложение [ править ]
Полезное асимптотическое разложение дополнительной функции ошибок (и, следовательно, также функции ошибок) для больших вещественных x :
где остаток в обозначениях Ландау равен
R N ( x ) = O ( x 1 − 2 N e − x 2 ) <\displaystyle R_
Действительно, точное значение остатка равно
что легко следует по индукции, записывая
e − t 2 = − ( 2 t ) − 1 ( e − t 2 ) ′ <\displaystyle e^<-t^<2>>=-(2t)^<-1>\left(e^<-t^<2>>\right)’>
и интеграция по частям.
Продолжение дроби [ править ]
Цепная дробь расширение дополнительной функции ошибок является следующим : [9]
Интеграл функции ошибок с функцией плотности Гаусса [ править ]
Из Нг и Геллера, формула 13 в разделе 4.3. [10]
Факториальный ряд [ править ]
Численные приближения [ править ]
Аппроксимация с элементарными функциями [ править ]
Полином [ править ]
Приближение с максимальной ошибкой для любого действительного аргумента: [22] 1.2 × 10 − 7 <\displaystyle 1.2\times 10^<-7>>
τ = t ⋅ exp ( − x 2 − 1.26551223 + 1.00002368 t + 0.37409196 t 2 + 0.09678418 t 3 − 0.18628806 t 4 + 0.27886807 t 5 − 1.13520398 t 6 + 1.48851587 t 7 − 0.82215223 t 8 + 0.17087277 t 9 ) <\displaystyle <\begin
Таблица значений [ править ]
| Икс | erf (x) | 1-эрф (х) |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022 564 575 | 0,977 435 425 |
| 0,04 | 0,045 111 106 | 0,954 888 894 |
| 0,06 | 0,067 621 594 | 0,932 378 406 |
| 0,08 | 0,090 078 126 | 0,909 921 874 |
| 0,1 | 0,112 462 916 | 0,887 537 084 |
| 0,2 | 0,222 702 589 | 0,777 297 411 |
| 0,3 | 0,328 626 759 | 0,671 373 241 |
| 0,4 | 0,428 392 355 | 0,571 607 645 |
| 0,5 | 0,520 499 878 | 0,479 500 122 |
| 0,6 | 0,603 856 091 | 0,396 143 909 |
| 0,7 | 0,677 801 194 | 0,322 198 806 |
| 0,8 | 0,742 100 965 | 0,257 899 035 |
| 0,9 | 0,796 908 212 | 0,203 091 788 |
| 1 | 0,842 700 793 | 0,157 299 207 |
| 1.1 | 0,880 205 07 | 0,119 794 93 |
| 1.2 | 0,910 313 978 | 0,089 686 022 |
| 1.3 | 0,934 007 945 | 0,065 992 055 |
| 1.4 | 0,952 285 12 | 0,047 714 88 |
| 1.5 | 0,966 105 146 | 0,033 894 854 |
| 1.6 | 0,976 348 383 | 0,023 651 617 |
| 1,7 | 0,983 790 459 | 0,016 209 541 |
| 1,8 | 0,989 090 502 | 0,010 909 498 |
| 1.9 | 0,992 790 429 | 0,007 209 571 |
| 2 | 0,995 322 265 | 0,004 677 735 |
| 2.1 | 0,997 020 533 | 0,002 979 467 |
| 2.2 | 0,998 137 154 | 0,001 862 846 |
| 2.3 | 0,998 856 823 | 0,001 143 177 |
| 2,4 | 0,999 311 486 | 0,000 688 514 |
| 2,5 | 0,999 593 048 | 0,000 406 952 |
| 3 | 0,999 977 91 | 0,000 022 09 |
| 3.5 | 0,999 999 257 | 0,000 000 743 |
Связанные функции [ править ]
Дополнительная функция ошибки [ править ]
Функция мнимой ошибки [ править ]
Кумулятивная функция распределения [ править ]
Φ ( x ) = 1 2 π ∫ − ∞ x e − t 2 2 d t = 1 2 [ 1 + erf ( x 2 ) ] = 1 2 erfc ( − x 2 ) <\displaystyle \Phi (x)=<\frac <1><\sqrt <2\pi >>>\int _<-\infty >^
или переставил для erf и erfc:
Стандартный нормальный cdf чаще используется в вероятностях и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера и также может быть выражена как конфлюэнтная гипергеометрическая функция ( функция Куммера):
Обобщенные функции ошибок [ править ]
Некоторые авторы обсуждают более общие функции: [ необходима цитата ]
Эти обобщенные функции могут быть эквивалентно выражены для x > 0 с использованием гамма-функции и неполной гамма-функции :
Следовательно, мы можем определить функцию ошибок в терминах неполной гамма-функции:
Итерированные интегралы дополнительной функции ошибок [ править ]
Повторные интегралы дополнительной функции ошибок определены в [27]
Общая рекуррентная формула
У них есть степенной ряд
откуда следуют свойства симметрии
Иллюстрированный самоучитель по Mathematica 3/4
Интегральные показательные и родственные им функции
К другой известной группе специальных функций относятся интегральные показательные и родственные им функции:
Ниже представлены примеры применения этих функций.
| Ввод (In) | Вывод (Out) |
|---|---|
| Coshlntegral[1.] | 0.837867 |
| Coslntegral [1. ] | 0.337404 |
| Erf[l.] | 0.842701 |
| Erf [2. +1*3.] | -20.8295 + 8.68732 I |
| Erf[2.,3.] | 0.00465564 |
| Erfc[l.] | 0.157299 |
| Erfi[l.] | 1.65043 |
| ExplntegralE [3.1.] | 0.109692 |
| ExpIntegralEi [1. ] | 1.89512 |
| Loglntegral [2. +3. *I ] | 2.3374 + 2.51301 I |
| Sinhlntegral [1. ] | 1.05725 |
| Sinlntegral [1. ] | 0.946083 |
На рис. 6.4 представлены графики ряда интегральных показательных функций, дающие представление об их поведении при вещественном аргументе.
Следует обратить внимание на то, что большая часть этих функций может иметь комплексный аргумент. Для получения численных значений функций нужно задавать аргумент в форме вещественного числа или комплексного числа с вещественными действительной и мнимой частями.

Рис. 6.4. Графики интегральных показательных функций
Документация
Синтаксис
Описание
Примеры
Функция ошибок для с плавающей точкой и символьных чисел
В зависимости от его аргументов, erf может возвратить или точные символьные результаты с плавающей точкой.
Вычислите функцию ошибок для этих чисел. Поскольку эти числа не являются символьными объектами, вы получаете результаты с плавающей точкой:
Вычислите функцию ошибок для тех же чисел, преобразованных в символьные объекты. Для большинства символьных (точных) чисел, erf отвечает на неразрешенные символьные звонки:
Использование vpa аппроксимировать символьные результаты необходимым количеством цифр:
Функция ошибок для переменных и выражений
Для большинства символьных переменных и выражений, erf отвечает на неразрешенные символьные звонки.
Вычислите функцию ошибок для x и sin(x) + x*exp(x) :
Функция ошибок для векторов и матриц
Если входной параметр является вектором или матрицей, erf возвращает функцию ошибок для каждого элемента того вектора или матрицы.
Вычислите функцию ошибок для элементов матричного M и векторный V :
Специальные значения функции ошибок
erf возвращает специальные значения для конкретных параметров.
Вычислите функцию ошибок для комплексных бесконечностей. Использование sym преобразовывать комплексные бесконечности в символьные объекты:
Обработка выражений, которые содержат функцию ошибок
Вычислите первые и вторые производные функции ошибок:
Вычислите интегралы этих выражений:
Постройте функцию ошибок
Постройте функцию ошибок на интервале от-5 до 5.
Входные параметры
X входной параметр
символьное число | символьная переменная | символьное выражение | символьная функция | символьный вектор | символьная матрица
Введите в виде символьного числа, переменной, выражения или функции, или как вектор или матрица символьных чисел, переменных, выражений или функций.
Больше о
Функция ошибок
Следующий интеграл задает функцию ошибок:
e r f ( x ) = 2 π ∫ 0 x e − t 2 d t
Советы
Вызов erf для номера, который не является символьным объектом, вызывает MATLAB ® erf функция. Эта функция принимает действительные аргументы только. Если вы хотите вычислить функцию ошибок для комплексного числа, использовать sym преобразовывать тот номер в символьный объект, и затем вызывать erf для того символьного объекта.
Алгоритмы
erf(erfinv(x)) = erfc(erfcinv(x)) = x
Ссылки
[1] Gautschi, W. “Функция ошибок и Интегралы Френели”. Руководство Математических функций с Формулами, Графиками и Математическими Таблицами. (М. Абрамовиц и я. А. Стегун, редакторы). Нью-Йорк: Дувр, 1972.
Смотрите также
Открытый пример
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
Документация Symbolic Math Toolbox
Поддержка
© 1994-2021 The MathWorks, Inc.
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.