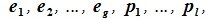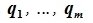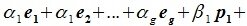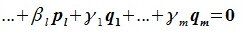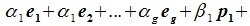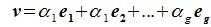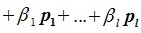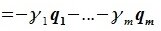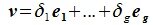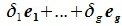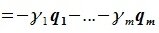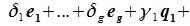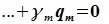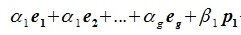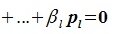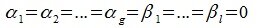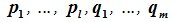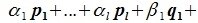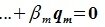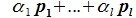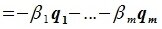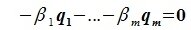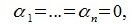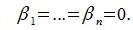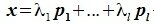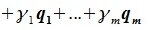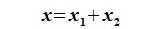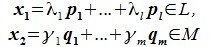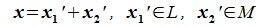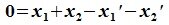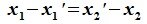Что такое dim в линейной алгебре
Подпространство линейного пространства
Определение и размерность подпространства
Определение 6.1. Подпространством L n-мерного пространства R называется множество векторов, образующих линейное пространство по отношению к действиям, которые определены в R.
Другими словами, L называется подпространством пространства R, если из x, y∈L следует, что x+y∈L и если x∈L, то λ x∈L, где λ— любое вещественное число.
Простейшим примером подпространства является нулевое подпространство, т.е. подмножество пространства R, состоящее из единственного нулевого элемента. Подпространством может служить и все пространство R. Эти подпространства называются тривиальными или несобственными.
Подпространство n-мерного пространства конечномерно и его размерность не превосходит n: dim L≤ dim R.
Сумма и пересечение подпространств
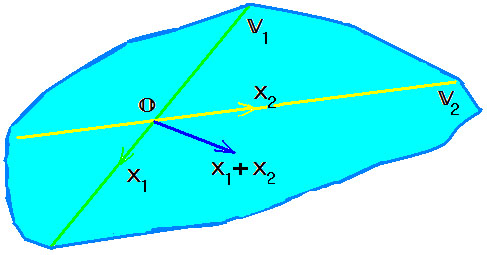
Cуммой L+M называется множество векторов x+y, где x∈L и y∈M. Очевидно, что любая линейная комбинация векторов из L+M принадлежит L+M, следовательно L+M является подпространством пространства R (может совпадать с пространством R).
Пересечением L∩M подпространств L и M называется множество векторов, принадлежащих одновременно подпространствам L и M (может состоять только из нулевого вектора).
Теорема 6.1. Сумма размерностей произвольных подпространств L и M конечномерного линейного пространства R равна размерности суммы этих подпространств и размерности пересечения этих подпространств:
dim L+dim M=dim(L+M)+dim(L∩M).
Доказательство. Обозначим F=L+M и G=L∩M. Пусть G g-мерное подпространство. Выберем в нем базис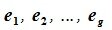 
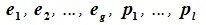
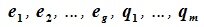
. Так как G⊂L и G⊂M, следовательно базис G можно дополнить до базиса L и до базиса M. Пусть 
базис подпространства L и пусть 
базис подпространства M. Покажем, что векторы
составляют базис F=L+M. Для того, чтобы векторы (6.1) составляли базис пространства F они должны быть линейно независимы и любой вектор пространства F можно представить линейной комбинацией векторов (6.1).
Докажем линейную независимость векторов (6.1). Пусть нулевой вектор пространства F представляется линейной комбинацией векторов (6.1) с некоторыми коэффициентами:
Левая часть (6.3) является вектором подпространства L, а правая часть является вектором подпространства M. Следовательно вектор
принадлежит подпространству G=L∩M. С другой стороны вектор v можно представить линейной комбинацией базисных векторов подпространства G:
Из уравнений (6.4) и (6.5) имеем:
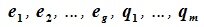
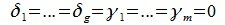
Но векторы являются базисом подпространства M, следовательно они линейно независимы и 
. Тогда (6.2) примет вид:
В силу линейной независимости базиса подпространства L имеем:
Так как все коэффициенты в уравнении (6.2) оказались нулевыми, то векторы
Изучая базисы подпространств L и M и базис подпространства F=L+M (6.10), имеем: dim L=g+l, dim M=g+m, dim (L+M)=g+l+m. Следовательно:
dim L+dim M−dim(L∩M)=dim(L+M). ■
Прямая сумма подпространств
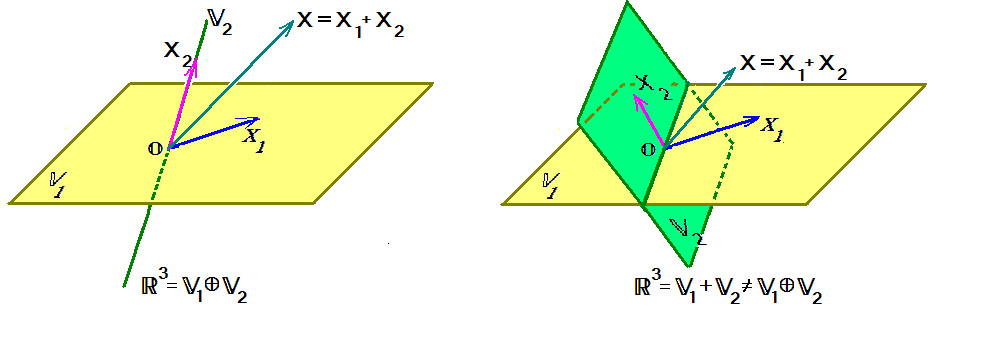
Определение 6.2. Пространство F представляет собой прямую сумму подпространств L и M, если каждый вектор x пространства F может быть единственным способом представлен в виде суммы x=y+z, где y∈ L и z∈M.
Прямая сумма обозначается L⊕M. Говорят, что если F=L⊕M, то F разлагается в прямую сумму своих подпространств L и M.
Теорема 6.2. Для того, чтобы n-мерное пространство R представляло собой прямую сумму подпространств L и M, достаточно, чтобы пересечение L и M содержало только нулевой элемент и чтобы размерность R была равна сумме размерностей подпространств L и M.
Доказательство. Выберем некоторый базис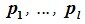 
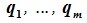
в подпространстве L и некоторый базис 
в подпространстве M. Докажем, что
является базисом пространства R. По условию теоремы размерность пространства R n равна сумме подпространств L и M (n=l+m). Достаточно доказать линейную независимость элементов (6.11). Пусть нулевой вектор пространства R представляется линейной комбинацией векторов (6.11) с некоторыми коэффициентами:
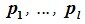
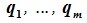
Но векторы и являются базисами подпространств L и M соответственно. Следовательно они линейно независимы. Тогда
Установили, что (6.12) справедливо лишь при условии (6.15), а это доказывает линейную независимость векторов (6.11). Следовательно они образуют базис в R.
Пусть x∈R. Разложим его по базису (6.11):
Из (6.17) и (6.18) следует, что любой вектор из R можно представить суммой векторов x1∈L и x2∈M. Остается доказать что это представление является единственным. Пусть кроме представления (6.17) есть и следующее представление:
Вычитая (6.19) из (6.17), получим
Так как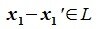 
, 
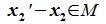
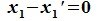
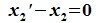
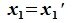
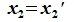
и L∩M= 0, то 
и 
. Следовательно 
и 
. ■
Размерность и базис линейного пространства
Определения размерности и базиса
Базисом n-мерного линейного пространства называется упорядоченная совокупность линейно независимых векторов ( базисных векторов ).
и притом единственным образом, т.е. коэффициенты определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.
Теорема 8.2 о дополнении системы векторов до базиса. Всякую линейно независимую систему векторов n-мерного линейного пространства можно дополнить до базиса пространства.
2. В некоторых пространствах, часто встречающихся в приложениях, один из возможных базисов, наиболее удобный с практической точки зрения, называют стандартным.
3. Теорема 8.1 позволяет говорить, что базис — это полная система элементов линейного пространства, в том смысле, что любой вектор пространства линейно выражается через базисные векторы.
5. Теорема 8.2 позволяет говорить, что базис — это максимальная линейно независимая система векторов линейного пространства, так как базис — это линейно независимая система векторов, и ее нельзя дополнить каким-либо вектором без потери линейной независимости.
Примеры базисов линейных пространств
Укажем размерность и базис для примеров линейных пространств, рассмотренных выше.
5. В пространстве матриц размеров можно выбрать 6 матриц:
которые линейно независимы. Действительно, их линейная комбинация
6. Для любого натурального в пространстве многочленов с комплексными коэффициентами можно найти п линейно независимых элементов. Например, многочлены линейно независимы, так как их линейная комбинация
Во-первых, покажем, что система линейно независима. В самом деле, возьмем линейную комбинацию этих ковекторов и приравняем ее нулевой функции
т.е. функция представлена в виде линейной комбинации функций (числа — коэффициенты линейной комбинации). Следовательно, система ковекторов является базисом сопряженного пространства и (для конечномерного пространства ).
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Благодарю Ю.А.Смолькина за обнаружение 07.08.19 ошибки на настоящей странице и информирование о ней.
Линейное пространство
Определения
Примеры линейных пространств
Почему множество решений системы неоднородных уравнений не образует линейного подпространства?
В пространстве квадратных матриц фиксированного порядка каждое из следующих подмножеств составляет линейное подпространство: симметричных, кососимметричных, верхнетреугольных, нижнетреугольных и диагональных матриц.
Изоморфизм
Линейная зависимость, базис, координаты
Пример. Для полиномов нескольких переменных свойство линейной зависимости является частным проявлением более общего свойства функциональной зависимости. Так, однородные полиномы (формы)
Теорема 2. а) Если система содержит хотя бы один нулевой вектор, то она л.з.
б) Если система л.н.з., то и любая ее подсистема л.н.з.
Две системы векторов называются эквивалентными если каждый вектор одной системы линейно выражается через векторы другой и обратно.
Теорема 4. Системы векторов
Теорема 5. Если каждая из двух эквивалентных систем
Пример [1]. Замечательный пример трехмерного линейного пространства дает нам совокупность всех цветов. Под суммой двух цветов будем понимать цвет, образованный их смешением
Анимация ☞ ЗДЕСЬ (1500 K, gif)
Пример. Найти базис подпространства
Ответ. Базис составляют, например, первая, вторая и четвертая строки.
Найти координаты полинома
Критерии линейной зависимости
Относительный базис
Сумма и пересечение линейных подпространств
Понятие пересечения линейных подпространств совпадает с понятием пересечения их как множеств.
Теорема. Имеет место формула:
Доказательство ☞ ЗДЕСЬ.
Можно ли обобщить этот результат на случай трех (и более подпространств)? Cправедлив ли, к примеру, аналог формулы включений-исключений в следующем виде:
Теорема. Имеет место формула:
Пример. Найти базис суммы и размерность пересечения
Найти базисы суммы и пересечения подпространств
Решение ☞ ЗДЕСЬ.
Прямая сумма линейных подпространств
Пример [2]. Доказать, что сумма подпространств
Линейные многообразия
Некоторые задачи на линейные многообразия ☞ ЗДЕСЬ.
Русские Блоги
MIT линейная алгебра линейная алгебра открытый класс ноты глава 9 линейная корреляция, база, размерность (лекция 9 независимость, основание и размерность)
В этой главе записка MIT линейной алгебры Gilbert Strang.Веб-сайт курса MIT линейной алгебрыОткрытое обмен лекций Сводка (PDF) и лекции Видеокрасина (PDF) и т. Д. И т. Д. Инструкции выглядят следующим образом, большинство содержимого заметок отВеб-сайт курса MIT линейной алгебрыНаправлено в информации, я просто закончу содержимое программы в течение курса в качестве текстовой формы. Передняя глава можно найти в некоторых других блогах (этот штамп »Глава Один，Глава вторая，третья глава，Глава четвертая，Глава пять，Глава шесть，Глава VII.，Глава восьми) Следующие главы будут обновлены в порядок видео
Каталог статьи
lecture 9 Independence, Basis and Dimension
1 линейная независимость
Независимость называется линейной независимостью;
1.1 Определение
1.2 Определите, не зависит ли линейный
Причина решения: должна быть свободная переменная (по крайней мере, одна)
Вообще говоря, набор векторных линейных линейных не связан, а матрица является линейной независимой. Что нас интересует, связаны ли столбец матрицы, если нулевое пространство N ( A ) N(A) N ( A ) Существует ненулевой вектор, то столбцы матрицы связаны.
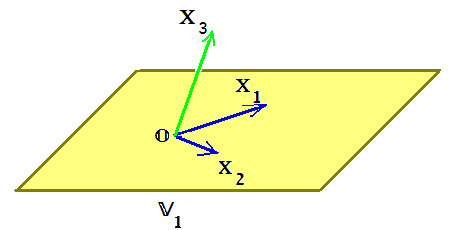
Two vectors are independent if they do not lie on the same line. Three vectors are independent if they do not lie in the same plane.
Example 1：
Если нулевая векторная группа содержит нулевой вектор, этот набор вектора связан.
Предположим, что два вектора в двумерном пространстве показаны ниже, v 1 v_1 v 1 и v 2 v_2 v 2 Комбинация не может получить нулевой вектор (за исключением нулевой комбинации), поэтому они независимости. 
2 «генерировать» пространство (охватывающее пространство)
— векторное поколение группы или расширение (охватывает пространство), что это значит?
Положите результат всех линейных комбинаций векторной группы в пространстве «просто» сгенерирован ».
Например, для пространства колонны матрицы обнаружены все линейные комбинации столбца матрицы, вектором столбца матрицы генерирует пространство столбца, что может быть связано или нет.
3 базы и размерность (основа и измерение)
3.1 База
То, что мы наиболее обеспокоены, состоит в том, что он может генерировать пространство, то есть независимо от векторной группы, то есть количество векторов должно быть уместно. Если число недостаточно, невозможно создать необходимое пространство. Если есть Слишком много, они не являются линейными независимыми. Следовательно, концепция «базы» предлагается, а количество векторов, которые он содержит, не так много.
3.1.1 Определение
The basis of a space tells us everything we need to know about that space.
Example 2： R 3 \mathcal
Поскольку эта группа не единственная группа, вы можете упомянуть другую группу:
— Как я могу проверить? (Откуда вы знаете, могут ли они представлять собой группу?)
— Вы можете сформировать матрицу в качестве столбца матрицы, затем выполните параметр и преобразование строки в матрицу, см. Если есть бесплатная переменная, будь то главная колонна;
— Могут ли они представлять собой группу?
— Нет, потому что двое из матриц, которые они делают, там будут нулевые линии, поэтому эти три векторы не являются линейно независимыми, поэтому они не могут быть; 3 × 3 3×3 3 × 3 Квадратный массив должен быть обратимым, и его колонна может образовывать основу.
Колонка с нерелированной колонкой точно создает пространство матрицы, им нечего делать, так что это основание пространства колонны.
3.1.2 ОСОБЕННОСТИ
3.2 Размер
Пространственная соответствующая группа имеет много групп, но количество векторов в каждой группе одинаково, и количество векторов в основании является размер пространства. Учитывая пространство, каждое основание для этого пространства имеет одинаковое количество вектора; это числоthe dimension of the space.
3.3 Резюме
Линейный независимый: ненулевая линейная комбинация не 0 0 0
Генерация: все линейные комбинации
База: набор нерелевантных векторов и генерирует пространство
Размер космического пространства: количество базового вектора (все количество векторных чисел)
4 столбца пространства и нулевого пространства (основания пространства колонны и нулевое пространство)
4.1 Основы колонны
— Могут ли они генерировать пространство колонны матрицы?
— Может, это определение пространства колонны.
— Это основание колонны?
— Найти группу групп для колонны пространства этой матрицы?
— Найдите другую группу баз в этом колонне пространстве?
4.2 Основы nullspace
Вектор нулевое пространство сообщает нам: как объединить вектор столбца, чтобы получить нулевой вектор, как эти столбцы будут линейно коррелировать.
Example 4：
— Это два специальных решения набор нулевого пространства? (Это нулевое пространство, состоящее из всех комбинаций этих двух векторов?)
Интеллектуальная рекомендация
Как сделать ваши данные PPT из Python?
Нажмите на «Программирование«Выберите набор наУстановить как звездный стандарт” Качественные статьи, впервые доставка! Автор: Костас Андреу Компиляция сердца машины Участие: Джамин, Ч.
Jquery plugin orgchart для достижения приема дисплея многократной структуры деревьев
Требования: передняя стойка реализует графическое отображение нескольких узлов деревьев, а некоторая информация сохраняется на узле для формирования серии JSON к обрабатыванию фона. &nbs.
Использование динамических разрешений и анализ исходного кода RxPermissions
Основное использование После Android 6.0 была добавлена динамическая конфигурация разрешений. Цель состоит в том, что пользователи могут свободно выбирать, предоставлять ли разрешения приложения. Да.
Анализ исходного кода Dubbo (11) Обменник Dubbo
Посмотри сначалаExchangerОпределение интерфейсаbindс участиемconnect ，bindОн вызывается сервером и связывает порт для приема запросов от клиента.connectЭто как клиент для подключения к серверу и обмен.
Разница между формальными параметрами и фактическими параметрами в Java
1. Используйте в функции: Формальный параметр появляется в определении функции и может использоваться во всем теле функции, но не может использоваться вне функции. Фактический параметр появляется в ос.
Что такое DIM линейная алгебра?
Почему линейная алгебра?
Что означает DIM в математике?
dim — это размерность векторного пространства
Что такое ker в линейной алгебре?
Множество векторов x линейного пространства X, которые оператор A отображает в нуль пространства Y, называется ядром оператора A: Ker(A) =
Где используется алгебра?
Вместе с фундаментальной ролью внутри математики алгебра применяется в прикладных областях. Теория представлений групп используется в физике, дискретные группы применяются в кристаллографии. Алгебраические методы используются в криптографии, теории кодирования, математической экономике.
В каком классе проходят линейную алгебру?
Программа элективного курса.
Как понять общую алгебру?
Общая алгебра (также абстрактная алгебра, высшая алгебра) — раздел математики, изучающий алгебраические системы (также иногда называемые алгебраическими структурами), такие как группы, кольца, поля, модули, решётки, а также отображения между такими структурами.
Что означает буква А в математике?
Что такое DIM Линал?
Число k называется размерностью линейного пространства L, если в L существует система из k линейно независимых векторов, а любая система из k+1 вектора — линейно зависима. Обозначается dimL = k.
Как в математике обозначается любое число?
ℕ — обозначение множества всех натуральных чисел. ℤ — множество целых чисел. Оно состоит из натуральных чисел, им противоположных и нуля.
Что такое Ker f?
Что такое TR в матрицах?
Что представляет собой ядро?
Клеточное ядро — центральный органоид эукариотической клетки, содержащий хромосомы. Ядро (ботаника) — внутренняя часть плодов и семян, заключённая в твёрдую оболочку.