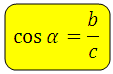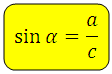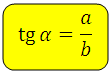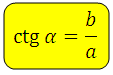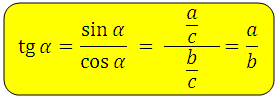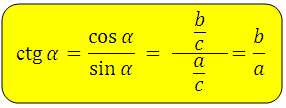Что такое cos в физике

Дайте пожалуйста полный ответ что такое косинус. )) ) Физика

Экономическая культура современного человека, являющаяся частью общей культуры, продолжает развиваться и расширять сферу своего влияния, что обусловлено ростом мировой экономики. В современное время актуально рассмотрение нравственного аспекта экономической культуры. Ведь мораль и нравственность выступают ограничителем, не позволяющим экономическому аспекту деятельности человеческого сообщества привести к общей катастрофе (например, экологической).

Экономическая культура человека определяет его мышление, поступки, действия в экономической сфере. Экономическая культура является базисом для формирования и апробации новых экономических идей, направленных на повышение эффективности данной сферы. Позитивные показатели состояния экономической культуры человека и общества свидетельствуют об их потенциальных возможностях в сфере трудовых ресурсов и в иных экономических сферах деятельности. Достижения экономической культуры человечества отражены как в материальных (суперсовременные здания, корпорации и т.д.), так и в духовных носителях (современные ноу-хау, научно-технический интеллектуальный продукт).

Повышение показателей экономической культуры человека, общества и государства усиливает степень конкурентоспособности хозяйствующих субъектов в сфере экономики, повышает качество товаров, услуг, оптимизирует соотношение «цена-качество», увеличивает покупательную способность и благосостояние граждан. Рост экономической культуры населения благоприятным образом сказывается на показателях экономики, отражающих ожидание граждан. Центрами культивирования экономической культуры, несомненно, являются учреждения среднего, высшего, дополнительного и послевузовского профессионального образования. Молодое поколение, вливаясь в общество со студенческой скамьи, привносит новые образцы экономической культуры, которые затем апробируются на практике, изме

Синусом называется отношение
Косинусом называется отношение
Тангенс определяется как
Котангенс определяется как
Секанс определяется как
Косеканс определяется как

Источник

Коэффициент мощности cos φ: определение, назначение, физический смысл

Коэффициент мощности – это скалярная физическая величина, показывающая насколько рационально потребителями расходуется электрическая энергия. Другими словами, коэффициент мощности описывает электроприемники с точки зрения присутствия в потребляемом токе реактивной составляющей.

В этой статье мы рассмотрим физическую сущность и основные методы определения cos φ.

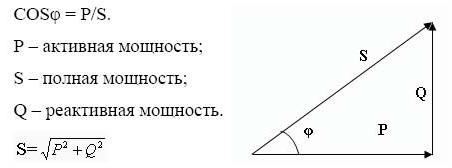
Математически cos φ

Математически cos φ определяется как отношение активной мощности к полной или равен отношению косинуса этих величин (отсюда и название параметра).

Величина коэффициента мощности может изменяться в интервале 0 — 1 (либо в диапазоне 0 — 100%). Чем ближе его величина к 1, тем лучше, поскольку при величине cos φ = 1 – потребителем реактивная мощность не потребляется (равняется 0), следовательно, меньше потребляемая полная мощность в общем.

Низкий cos φ указывает на то, что на внутреннем сопротивлении потребителя выделяется повышенная реактивная мощность.

Когда токи / напряжения являются идеальными сигналами синусоидальной формы, то коэффициент мощности составляет 1.

Геометрически коэффициент мощности можно изобразить, как косинус угла на векторной диаграмме между током, напряжением между током, напряжением. В связи с чем при синусоидальной форме токов и напряжений величина cos φ совпадает с косинусом угла, от которого отстают эти фазы.

Короткое видео о кратким объяснением, что такое коэффициент мощности:

Повышение коэффициента мощности

Значение коэффициента мощности рассчитывают при проектировании сетей. Поскольку низкое его значение является следствием увеличения величины общих потерь электроэнергии. Для его увеличения в сетях используют различные способы коррекции, повышая его значение до 1.

Повышение cos φ преследует 3 основные задачи:

Технически коррекция реализуется в виде введения различных дополнительных схем на вход устройств. Эта техника требуется для равномерного использования мощности фазы, устранения перегрузок нулевого провода 3-х-фазной сети, и является обязательной для импульсных источников питания, установленной мощностью 100 Вт и более.

Основные способы коррекции cos φ

1. Коррекция реактивной составляющей мощности производится путём включения реактивного элемента, имеющего противоположное действие. К примеру, для компенсации работы асинхронной машины, обладающей высокой индуктивной реактивной составляющей мощности, в параллель включается конденсатор.

2. Корректировка нелинейности электропотребления. При потреблении тока нагрузкой непропорционально основной гармонике напряжения, для повышения коэффициента мощности в схему вводят пассивный (активный) корректор коэффициента мощности. Наиболее простым примером пассивного корректора cos φ является дроссель с высокой индуктивностью, подключаемый последовательно с нагрузкой. Дроссель производит сглаживание импульсного потребления нагрузки и создание низшей, основной гармоники тока.

3. Корректировка естественным способом, не предусматривающая установку дополнительных устройств, предполагает упорядочение технологического процесса, рациональное распределение нагрузок, ведущее к улучшению режима потребления электроэнергии оборудованием, повышению коэффициента мощности.

Подробное видео с объяснением, что такое cosφ :

Источник

Что такое cos в физике

Тригонометрия в физике.

Автор работы награжден дипломом победителя III степени

Актуальность: Данная тема, бесспорно, является актуальной. Тригонометрия использовалась людьми за много лет до нашей эры, уже тогда без знания этой науки было невозможно построить дом, а астрономам не удавалось провести различные расчеты. Спустя тысячелетия ничего не изменилось, тригонометрия по-прежнему остается одной из самых нужных наук, поэтому ее основы должен знать каждый человек, для того чтобы производить расчеты и иметь представление о самых элементарных функциях, так как тригонометрия заставляет думать логически и концентрирует наше внимание.

Цель: Определение связи тригонометрии с окружающим миром.

1.Рассмотреть историю возникновения и развития тригонометрии.

2.Показать на примерах практическое применение тригонометрии в физике.

3.Раскрыть на примерах возможности использования тригонометрических функций.

Гипотеза: Большинство физических явлений природы, физиологических процессов, закономерностей в музыке и искусстве можно описать с помощью тригонометрии и тригонометрических функций.

Практическая значимость: проект может использоваться в качестве теоретического курса в качестве дополнения, закрепления уже пройденного материала или на внеурочных занятиях.

1.История возникновения тригонометрии

Зачатки тригонометрии можно найти в математических рукописях древнего Египта, Вавилона и древнего Китая. 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.

От вавилонской математики ведёт начало привычное нам измерение углов градусами, минутами и секундами (введение этих единиц в древнегреческую математику обычно приписывают Гипсиклу, II век до н. э.).

Среди известных вавилонянам теорем была, например, такая: вписанный угол, опирающийся на диаметр круга — прямой. Главным достижением этого периода стало соотношение, позже получившее название теоремы Пифагора. Неизвестно, знали ли общую формулировку теоремы древние египтяне, но прямоугольный «египетский треугольник» со сторонами 3, 4 и 5 был там хорошо известен и широко использовался.

Общее и логически связное изложение тригонометрических соотношений появилось в древнегреческой геометрии. Греческие математики ещё не выделяли тригонометрию как отдельную науку, для них она была частью астрономии. Впервые само слово тригонометрия встречается в 1505 году в заглавии книги немецкого математика Питискуса.

Основным достижением античной тригонометрической теории стало решение в общем виде задачи «решения треугольников», то есть нахождения неизвестных элементов треугольника, исходя из трёх заданных его элементов (из которых хотя бы один является стороной).

В данном случае измерение треугольников следует понимать как решение треугольников, т. е. определение сторон, углов и других элементов треугольника, если даны некоторые из них.

Возникновение тригонометрии связано с землемерением, астрономией и строительным делом.

Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10′ с точностью до 1/604. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.

Долгое время тригонометрия носила чисто геометрический характер, т. е. Факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Пожалуй, наибольшие стимулы к развитию тригонометрии возникали в связи с решением задач астрономии, что представляло большой практический интерес.

Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Громадное научное наследие Эйлера включает блестящие результаты, относящиеся к математическому анализу, геометрии, теории чисел, механике и другим приложениям математики. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее проще.

Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.

Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.

К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс, котангенс, секанс и косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция.

Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OМ и положительным направлением оси Ox равен α.

Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r:
sinα=y/r.
Поскольку r=1, то синус равен ординате точки M(x,y).

Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r:
cosα=x/r

Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x:
tanα=y/x,x≠0

Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
cotα=x/y,y≠0

Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y):
secα=r/x=1/x,x≠0

Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y):
cscα=r/y=1/y,y≠0

В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
Синусом угла α называется отношение противолежащего катета к гипотенузе.
Косинусом угла α называется отношение прилежащего катета к гипотенузе.
Тангенсом угла α называется противолежащего катета к прилежащему.
Котангенсом угла α называется прилежащего катета к противолежащему.
Секанс угла α представляет собой отношение гипотенузы к прилежащему катету.
Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету.

График функции синус
y=sinx, область определения: x∈R, область значений: −1≤sinx≤1

График функции косинус
y=cosx, область определения: x∈R, область значений: −1≤cosx≤1

График функции тангенс y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞

Старт в науке

Учредителями Конкурса являются Международная ассоциация учёных, преподавателей и специалистов – Российская Академия Естествознания, редакция научного журнала «Международный школьный научный вестник», редакция журнала «Старт в науке».

Источник

Как определить косинус или синус в физике

Дело в том, что я не раз наблюдал, как учащиеся 10-11 классов с трудом вспоминают данные определения. Они прекрасно помнят, что катет относится к гипотенузе, а вот какой из них — забывают и путают. Цена ошибки, как вы знаете на экзамене – это потерянный бал.

Информация, которую я представлю непосредственно к математике не имеет никакого отношения. Она связана с образным мышлением, и с приёмами словесно-логической связи. Именно так, я сам, раз и на всегда запомнил данные определения. Если вы их всё же забудете, то при помощи представленных приёмов всегда легко вспомните.

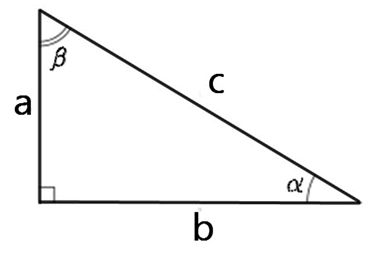
Напомню определения синуса и косинуса в прямоугольном треугольнике:

Косинус острого угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе:

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

Итак, какие ассоциации у вас вызывает слово косинус?

Наверное, у каждого свои 😉 Запоминайте связку:

Таким образом, у вас сразу в памяти возникнет выражение –

«… отношение ПРИЛЕЖАЩЕГО катета к гипотенузе ».

Проблема с определением косинуса решена.

Если нужно вспомнить определение синуса в прямоугольном треугольнике, то вспомнив определение косинуса, вы без труда установите, что синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе. Ведь катетов всего два, если прилежащий катет «занят» косинусом, то синусу остаётся только противолежащий.

Как быть с тангенсом и котангенсом? Путаница та же. Учащиеся знают, что это отношение катетов, но проблема вспомнить какой к которому относится – то ли противолежащий к прилежащему, то ли наоборот.

Тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему:

Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему:

Как запомнить? Есть два способа. Один так же использует словесно-логическую связь, другой – математический.

СПОСОБ МАТЕМАТИЧЕСКИЙ

Есть такое определение – тангенсом острого угла называется отношение синуса угла к его косинусу:

*Запомнив формулу, вы всегда сможете определить, что тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему.

Аналогично. Котангенсом острого угла называется отношение косинуса угла к его синусу:

Итак! Запомнив указанные формулы вы всегда сможете определить, что:

— тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему

— котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему.

СПОСОБ СЛОВЕСНО-ЛОГИЧЕСКИЙ

О тангенсе. Запомните связку:

То есть если потребуется вспомнить определение тангенса, при помощи данной логической связи, вы без труда вспомните, что это

«… отношение противолежащего катета к прилежащему»

Если речь зайдёт о котангенсе, то вспомнив определение тангенса вы без труда озвучите определение котангенса –

«… отношение прилежащего катета к противолежащему»

СПОСОБ УНИВЕРСАЛЬНЫЙ

Можно просто зазубрить. Но как показывает практика, благодаря словесно-логическим связкам человек запоминает информацию надолго, и не только математическую.

‘);> //–>
Тригонометрия – это раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии.

Синус (sin) – это тригонометрическая функция, геометрически представляющая отношение противолежащего катета к гипотенузе в прямоугольном треугольнике.

Косинус (cos) – это тригонометрическая функция, геометрически представляющая отношение прилежащего катета к гипотенузе в прямоугольном треугольнике.

Перевод синуса в косинус и обратно выполняется посредством решения основного тригонометрического тождества sin 2 (x) + cos 2 (x) = 1.

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор для перевода синуса в косинус (sin в cos). С помощью этого калькулятора вы в один клик сможете перевести косинус в синус (cos в sin) и обратно.

Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.

Синус, косинус, тангенс и котангенс. Определения

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Синус угла ( sin α ) – отношение противолежащего этому углу катета к гипотенузе.

Косинус угла ( cos α ) – отношение прилежащего катета к гипотенузе.

Тангенс угла ( t g α ) – отношение противолежащего катета к прилежащему.

Котангенс угла ( c t g α ) – отношение прилежащего катета к противолежащему.

Данные определения даны для острого угла прямоугольного треугольника!

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Угол поворота

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.

Синус (sin) угла поворота

При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t = y

Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t = x

Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

Тригонометрические функции углового и числового аргумента

Основные функции тригонометрии

Синус, косинус, тангенс и котангенс – основные тригонометрические функции.

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.

sin α = A 1 H O A 1 = y 1 = y

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Источник