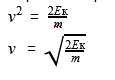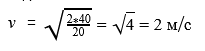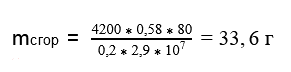Что такое const физика

Физические константы

Фундамента́льная физи́ческая постоя́нная (вар.: конста́нта) — физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Фундаментальные физические постоянные возникают при математическом описании окружающего мира с помощью теоретической физики. Часто сюда же относят и некоторые другие физические постоянные, так или иначе связанные с конкретными телами.

Слово «постоянная» подразумевает, что численное значение этой величины не меняется со временем. В реальности это может быть и не так (например, в последние годы появились свидетельства в пользу того, что постоянная тонкой структуры меняется в ходе эволюции Вселенной). Однако даже если эти величины и меняются со временем, то крайне медленно, и сколько-нибудь заметные изменения стоит ожидать лишь на масштабах порядка возраста Вселенной.

Стоит различать размерные и безразмерные физические постоянные. Численное значение размерной величины зависит от выбора единиц измерения. Численное же значение безразмерных постоянных более фундаментально, так как оно не зависит от системы единиц.

Содержание

Фундаментальные физические постоянные

Размерные комбинации фундаментальных постоянных

Название	Символ	Значение	Прим.
планковская масса		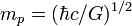2,176 44(11)×10 −8 кг	a
планковская длина		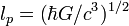1,616 252(81)×10 −35 м	a
планковское время		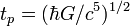5,391 24(27)×10 −44 с	a

Постоянные, связывающие разные системы единиц

Некоторые другие физические постоянные

Примечания

Ссылки

Полезное

Смотреть что такое «Физические константы» в других словарях:

ФИЗИЧЕСКИЕ КОНСТАНТЫ — (физические постоянные), постоянные величины, входящие в математические выражения физических законов (например, постоянная Авогадро). Физические константы, входящие в фундаментальные физические законы (например, всемирного тяготения закон) или… … Современная энциклопедия

ФИЗИЧЕСКИЕ КОНСТАНТЫ — (физические постоянные) постоянные величины, входящие в математические выражения физических законов (напр., газовая постоянная R в Клапейрона уравнении). Физические константы, входящие в фундаментальные физические законы (напр., закон всемирного… … Большой Энциклопедический словарь

Физические константы — (физические постоянные), постоянные величины, входящие в математические выражения физических законов (например, постоянная Авогадро). Физические константы, входящие в фундаментальные физические законы (например, всемирного тяготения закон) или… … Иллюстрированный энциклопедический словарь

ФИЗИЧЕСКИЕ КОНСТАНТЫ — см. Фундаментальные физические константы. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

физические константы — (физические постоянные), постоянные величины, входящие в математические выражения физических законов (например, газовая постоянная R в Клапейрона уравнении). Физические константы, входящие в фундаментальные физические законы (например, закон… … Энциклопедический словарь

физические константы — fizikinės konstantos statusas T sritis chemija apibrėžtis Pastovūs dydžiai, įeinantys į fizikos dėsnių matematines išraiškas. atitikmenys: angl. physical constants; universal constants rus. мировые константы; универсальные постоянные; физические… … Chemijos terminų aiškinamasis žodynas

ФИЗИЧЕСКИЕ КОНСТАНТЫ — (физические постоянные), пост. величины, входящие в матем. выражения физ. законов (напр., газ. постоянная R в Клапейрона уравнении). Ф. к., входящие в фундам. физ. законы (напр., закон всемирного тяготения) или являющиеся характеристиками частиц… … Естествознание. Энциклопедический словарь

Физические константы — то же, что Физические постоянные … Большая советская энциклопедия

Физические константы сложных виниловых эфиров — Виниловый эфир Температура кипения, °С/мм рт. ст. Плотность, г/см3 Показатель преломления, nD Винилформиат 46,6/760 0,9651* 1,4757* … Химический справочник

ФУНДАМЕНТАЛЬНЫЕ ФИЗИЧЕСКИЕ КОНСТАНТЫ — постоянные, входящие в ур ния, описывающие фундам. законы природы и свойства материи. Ф. ф. к. определяют точность, полноту и единство наших представлений об окружающем мире, возникая в теоретич. моделях наблюдаемых явлений в виде универсальных… … Физическая энциклопедия

Источник

Физическая константа

Фундамента́льная физи́ческая постоя́нная (вар.: конста́нта) — физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Фундаментальные физические постоянные возникают при математическом описании окружающего мира с помощью теоретической физики. Часто сюда же относят и некоторые другие физические постоянные, так или иначе связанные с конкретными телами.

Слово «постоянная» подразумевает, что численное значение этой величины не меняется со временем. В реальности это может быть и не так (например, в последние годы появились свидетельства в пользу того, что постоянная тонкой структуры меняется в ходе эволюции Вселенной). Однако даже если эти величины и меняются со временем, то крайне медленно, и сколько-нибудь заметные изменения стоит ожидать лишь на масштабах порядка возраста Вселенной.

Стоит различать размерные и безразмерные физические постоянные. Численное значение размерной величины зависит от выбора единиц измерения. Численное же значение безразмерных постоянных более фундаментально, так как оно не зависит от системы единиц.

Содержание

Фундаментальные физические постоянные

Размерные комбинации фундаментальных постоянных

Название	Символ	Значение	Прим.
планковская масса		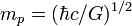2,176 44(11)×10 −8 кг	a
планковская длина		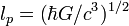1,616 252(81)×10 −35 м	a
планковское время		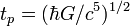5,391 24(27)×10 −44 с	a

Постоянные, связывающие разные системы единиц

Некоторые другие физические постоянные

Примечания

Ссылки

Полезное

Смотреть что такое «Физическая константа» в других словарях:

физическая константа — fizikinė konstanta statusas T sritis Standartizacija ir metrologija apibrėžtis Pastovus dydis, įeinantis į kurio nors fizikos dėsnio matematinę išraišką. atitikmenys: angl. physical constant vok. physikalische Konstante, f rus. физическая… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Фундаментальная физическая константа — Фундаментальная физическая постоянная (вар.: константа) физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Фундаментальные физические постоянные возникают при математическом описании окружающего… … Википедия

Константа — Константа: Постоянная Математическая Физическая Константа (в программировании) Константа диссоциации кислоты Константа равновесия Константа скорости реакции Константа (Остаться в живых) См. также Констанция Констанций Константин Констант… … Википедия

Константа диссоциации — Константа диссоциации вид константы равновесия, которая показывает склонность большого объекта диссоциировать (разделяться) обратимым образом на маленькие объекты, как например когда комплекс распадается на составляющие молекулы, или когда… … Википедия

КОНСТАНТА ВЗАИМОДЕЙСТВИЯ — (константа связи) (от лат. constans постоянный) в квантовой теории поля (КТП) параметр, определяющий силу (интенсивность) взаимодействия частиц или полей. В общем виде К. в. задаётся как значение вершинной части (вершины) при определ. значениях… … Физическая энциклопедия

Константа автопротолиза — Константа автопротолиза физическая величина, характеризующая способность протонного растворителя к диссоциации. Обозначается KS. Является произведением концентраций иона лиония и иона лиата. Так, например, для растворителя, который… … Википедия

Константа равновесия — У этого термина существуют и другие значения, см. Константа. Для улучшения этой статьи желательно?: Проверить достоверность указанной в статье информации … Википедия

ФИЗИЧЕСКАЯ ХИМИЯ — раздел химии, в котором изучаются химические свойства веществ на основе физических свойств составляющих их атомов и молекул. Современная физическая химия широкая междисциплинарная область, граничащая с различными разделами физики, биофизики и… … Энциклопедия Кольера

Константа диссоциации кислоты — У этого термина существуют и другие значения, см. Константа. Константа диссоциации кислоты (Ka) константа равновесия реакции диссоциации кислоты на ион водорода и анион кислотного остатка. Для многоосновных кислот, диссоциация которых… … Википедия

Действие (физическая величина) — У этого термина существуют и другие значения, см. Действие (физика). Действие Размерность L2MT−1 Действие в физике скалярная физическая величина, являющаяс … Википедия

Источник

КОНСТАНТА

Полезное

Смотреть что такое «КОНСТАНТА» в других словарях:

константа́н — константан … Русское словесное ударение

Константа — Константа: Постоянная Математическая Физическая Константа (в программировании) Константа диссоциации кислоты Константа равновесия Константа скорости реакции Константа (Остаться в живых) См. также Констанция Констанций Константин Констант… … Википедия

константа — • константа диссоциации константа нестойкости комплекса константа равновесия константа скорости реакции … Химические термины

КОНСТАНТА — [лат. constans (constantis) постоянный] постоянная величина (напр., в математике, физике, информатике (ИНФОРМАТИКА)). Словарь иностранных слов. Комлев Н.Г., 2006. константа (лат. constans (constants) постоянный) постоянная величина. Новый словарь … Словарь иностранных слов русского языка

КОНСТАНТА — (постоянная), в математике и других науках величина или коэффициент, не подвергающийся изменению. Константа может быть универсальной, как число (отношение окружности круга к его диаметру), или конкретной, как коэффициенты, введенные в… … Научно-технический энциклопедический словарь

Константа — элемент речевого ритма, повторяющийся с известным постоянством. Повторяясь в речевой динамике, К. является тем звуковым элементом, к рый определяет членение речи на те или иные повторяющиеся и соизмеримые отрезки, ритмические единицы, чередование … Литературная энциклопедия

Константа — в программировании элемент данных, который занимает место в памяти, имеет имя и определенный тип, причем его значение никогда не меняется. См. также: Языки программирования Финансовый словарь Финам … Финансовый словарь

константа — постоянная. Ant. переменная Словарь русских синонимов. константа сущ., кол во синонимов: 1 • постоянная (1) Словарь синонимов ASIS. В.Н. Тришин … Словарь синонимов

КОНСТАНТА — (от лат. constans постоянный) постоянная величина. Постоянство величины х символически записывают х=const. Константу часто обозначают буквами С и К … Большой Энциклопедический словарь

Источник

Закон сохранения механической энергии

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Энергия: что это такое

Если мы погуглим определение слова «Энергия», то скорее всего найдем что-то про формы взаимодействия материи. Это верно, но совершенно непонятно.

Поэтому давайте условимся здесь и сейчас, что энергия — это запас, который пойдет на совершение работы.

Энергия бывает разных видов: механическая, электрическая, внутренняя, гравитационная и так далее. Измеряется она в Джоулях (Дж) и чаще всего обозначается буквой E.

Механическая энергия

Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.

Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия.

Представьте, что вы взяли в руки канцелярскую резинку, растянули ее и отпустили. Из растянутого положения резинка просто «полетит», как только вы ей позволите это сделать. В этом процессе в момент натяжения резинка обладает потенциальной энергией, а в момент полета — кинетической.

Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим 😂), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия.

Кинетическая энергия

Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость.

Кинетическая энергия

Ек = (m*v^2)/2

Ек — кинетическая энергия [Дж]

Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия.

Задачка раз

Определить кинетическую энергию собаченьки массой 10 килограмм, если она бежала за мячом с постоянной скоростью 2 м/с.

Решение:

Формула кинетической энергии Ек = (m*v^2)/2

Ответ: кинетическая энергия пёсы равна 20 Дж.

Задачка два

Найти скорость бегущего по опушке гнома, если его масса равна 20 килограммам, а его кинетическая энергия — 40 Дж

Решение:

Формула кинетической энергии Ек = (m*v^2)/2

Ответ: гном бежал со скоростью 2 м/с.

Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!

Потенциальная энергия

В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия.

Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия.

Потенциальная энергия деформированной пружины

Еп — потенциальная энергия [Дж]

x — удлинение пружины [м]

Потенциальная энергия

Еп = mgh

Еп — потенциальная энергия [Дж]

g — ускорение свободного падения [м/с^2]

На планете Земля g ≃ 9,8 м/с^2

Задачка раз

Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с^2.

Решение:

Формула потенциальной энергии Еп = mgh

Eп = 0,1 * 9,8 * 2500=2450 Дж

Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж.

Задачка два

Найти высоту горки, с которой собирается скатиться лыжник массой 65 килограмм, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с^2.

Решение:

Формула потенциальной энергии Еп = mgh

Переведем 637 кДж в Джоули.

637 кДж = 637000 Дж

h = 637 000/(65 * 9,8) = 1000 м

Ответ: высота горы равна 1000 метров.

Задачка три

Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E1 и E2. Считать, что потенциальная энергия отсчитывается от уровня крышки стола.

Решение:

Потенциальная энергия вычисляется по формуле: E = mgh

Таким образом, получим, что

Ответ: E1 = E2.

Закон сохранения энергии

В физике и правда ничего не исчезает бесследно. Чтобы это как-то выразить, используют законы сохранения. В случае с энергией — Закон сохранения энергии.

Закон сохранения энергии

Полная механическая энергия замкнутой системы остается постоянной.

Полная механическая энергия — это сумма кинетической и потенциальной энергий. Математически этот закон описывается так:

Закон сохранения энергии

Еполн.мех. = Еп + Eк = const

Еполн.мех. — полная механическая энергия системы [Дж]

Еп — потенциальная энергия [Дж]

Ек — кинетическая энергия [Дж]

const — постоянная величина

Задачка раз

Мяч бросают вертикально вверх с поверхности Земли. Сопротивление воздуха пренебрежимо мало. Как изменится высота подъёма мяча при увеличении начальной скорости мяча в 2 раза?

Решение:

Должен выполняться закон сохранения энергии:

В начальный момент времени высота равна нулю, значит Еп = 0. В этот же момент времени Ек максимальна.

В конечный момент времени все наоборот — кинетическая энергия равна нулю, так как мяч уже не может лететь выше, а вот потенциальная максимальна, так как мяч докинули до максимальной высоты.

Это можно описать соотношением:

Еп1 + Ек1 = Еп2 + Ек2

Разделим на массу левую и правую часть

Из соотношения видно, что высота прямо пропорциональна квадрату начальной скорости, значит при увеличении начальной скорости мяча в два раза, высота должна увеличиться в 4 раза.

Ответ: высота увеличится в 4 раза

Задачка два

Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью v0, поднялось на максимальную высоту h0. Сопротивление воздуха пренебрежимо мало. Чему будет равна полная механическая энергия тела на некоторой промежуточной высоте h?

Решение

По закону сохранения энергии полная механическая энергия изолированной системы остаётся постоянной. В максимальной точке подъёма скорость тела равна нулю, а значит, оно будет обладать исключительно потенциальной энергией Емех = Еп = mgh0.

Таким образом, на некоторой промежуточной высоте h, тело будет обладать и кинетической и потенциальной энергией, но их сумма будет иметь значение Емех = mgh0.

Ответ: Емех = mgh0.

Задачка три

Мяч массой 100 г бросили вертикально вверх с поверхности земли с начальной скоростью 6 м/с. На какой высоте относительно земли мяч имел скорость 2 м/с? Сопротивлением воздуха пренебречь.

Решение:

Переведем массу из граммов в килограммы:

У поверхности земли полная механическая энергия мяча равна его кинетической энергии:

Е = Ек0 = (m*v^2)/2 = (0,1*6^2)/2 = 1,8 Дж

На высоте h потенциальная энергия мяча есть разность полной механической энергии и кинетической энергии:

mgh = E — (m*v^2)/2 = 1,8 — (0,1 * 2^2)/2 = 1,6 Дж

h = E/mg = 1,6/0,1*10 = 1,6 м

Ответ: мяч имел скорость 2 м/с на высоте 1,6 м

Переход механической энергии во внутреннюю

Внутренняя энергия — это сумма кинетической энергии хаотичного теплового движения молекул и потенциальной энергии их взаимодействия. То есть та энергия, которая запасена у тела за счет его собственных параметров.

Часто механическая энергия переходит во внутреннюю. Происходит этот процесс путем совершения механической работы над телом. Например, если сгибать и разгибать проволоку — она будет нагреваться.

Или если кинуть мяч в стену, часть энергии при ударе перейдет во внутреннюю.

Задачка

Какая часть начальной кинетической энергии мяча при ударе о стену перейдет во внутреннюю, если полная механическая энергия вначале в два раза больше, чем в конце?

Решение:

В самом начале у мяча есть только кинетическая энергия, то есть Емех = Ек.

В конце механическая энергия равна половине начальной, то есть Емех/2 = Ек/2

Часть энергии уходит во внутреннюю, значит Еполн = Емех/2 + Евнутр

Емех = Емех/2 + Евнутр

Ответ: во внутреннюю перейдет половина начальной кинетической энергии

Закон сохранения энергии в тепловых процессах

Чтобы закон сохранения энергии для тепловых процессов был сформулирован, было сделано два важных шага. Сначала французский математик и физик Жан Батист Фурье установил один из основных законов теплопроводности. А потом Сади Карно определил, что тепловую энергию можно превратить в механическую.

Вот что сформулировал Фурье:

При переходе теплоты от более горячего тела к более холодному температуры тел постепенно выравниваются и становятся едиными для обоих тел — наступает состояние термодинамического равновесия.

Таким образом, первым важным открытием было открытие того факта, что все протекающие без участия внешних сил тепловые процессы необратимы.

Дальше Карно установил, что тепловую энергию, которой обладает на­гретое тело, непосредственно невозможно превратить в механиче­скую энергию для производства работы. Это можно сделать, только если часть тепловой энергии тела с большей температурой передать другому телу с меньшей температурой и, следовательно, нагреть его до более высокой температуры.

Закон сохранения энергии в тепловых процессах

При теплообмене двух или нескольких тел абсолютное количество теплоты, которое отдано более нагретым телом, равно количеству теплоты, которое получено менее нагретым телом.

Математически его можно описать так:

Уравнение теплового баланса

Q отд = Q пол

Qотд — отданное системой количество теплоты [Дж]

Q пол — полученное системой количество теплоты [Дж]

Данное равенство называется уравнением теплового баланса. В реальных опытах обычно получается, что отданное более нагретым телом количество теплоты больше количества теплоты, полученного менее нагретым телом:

Это объясняется тем, что некоторое количество теплоты при теплообмене передаётся окружающему воздуху, а ещё часть — сосуду, в котором происходит теплообмен.

Задачка раз

Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С, если учесть, что на нагревание пошло 20% затраченной энергии.

Удельная теплота сгорания спирта 2,9·10^7Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С).

Решение:

При нагревании тело получает количество теплоты

где c — удельная теплоемкость вещества

При сгорании тела выделяется энергия

где q — удельная теплота сгорания топлива

По условию задачи нам известно, что на нагревание пошло 20% затраченной энергии.

Ответ: масса сгоревшего топливаа равна 33,6 г.

Задачка два

Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь. Удельная теплоемкость льда равна 2100 Дж/кг*℃, удельная теплота плавления льда равна 3,3*10^5 Дж/кг.

Решение:

Для нагревания льда до температуры плавления необходимо:

Qнагрев = 2100 * 0,5 * (10-0) = 10500 Дж

Для превращения льда в воду:

Qпл = 3,3 * 10^5 * 0,5 = 165000 Дж

Q = Qнагрев + Qпл = 10500 + 165000 = 175500 Дж = 175,5 кДж

Ответ: чтобы превратить 0,5 кг льда в воду при заданных условиях необходимо 175,5 кДж тепла.

Источник