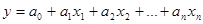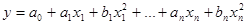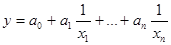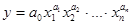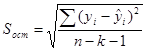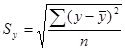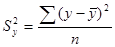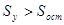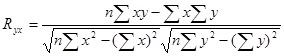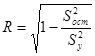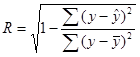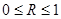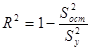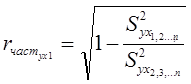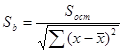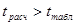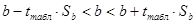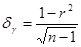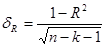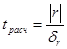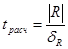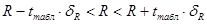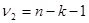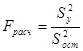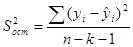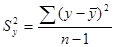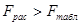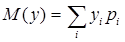Что такое blue оценка
Что такое оценка BLEU?
BLEU (Bilingual Evaluation Understudy) — это измерение различий между автоматическим переводом и одним или несколькими эталонными пользовательскими переводами одного исходного предложения.
Процесс оценки
Алгоритм BLEU сравнивает последовательные фразы автоматического перевода с последовательными фразами, которые он находит в эталонном переводе, и взвешенно подсчитывает количество совпадений. Эти совпадения не зависят от позиции. Высшая степень совпадения указывает на более высокую степень сходства с эталонным переводом и более высокий балл. Внятность и грамматика не учитываются.
Как работает BLEU
Преимущество алгоритма BLEU в том, что он хорошо коррелирует с оценками пользователей. Он усредняет число ошибок в отдельных предложениях для всего тестового набора, вместо того чтобы пытаться разработать точную оценку пользователя для каждого предложения.
Более подробные сведения об оценках BLEU см. в этой статье.
Результаты BLEU сильно зависят от обширности предметной области, согласованности тестовых данных с данными для обучения и настройки, а также от того, сколько данных у вас есть для обучения. Если модели были обучены в узкой предметной области, а ваши данные для обучения согласованы с тестовыми данными, вы можете ожидать высокую оценку BLEU.
Сравнение оценок BLEU оправдано только в том случае, когда результаты BLEU сравниваются с тем же тестовым набором, той же языковой парой и тем же модулем машинного перевода. Оценка BLEU из другого тестового набора должна отличаться.
Что такое blue оценка
Рассмотрим линейную регрессионную модель (г/, Х(3, а2 V), где /3 удовлетворяет совместным линейным ограничениям R/3 = г. Пусть V Ф 0. Тогда наилучшая линейная несмещенная оценка строго оцениваемой параметрической функции W/3 равна W/3, при этом [c.340]
Рассмотрим схему Гаусса-Маркова (у, Xf3, п- Он называется частным. [c.8]
Метод, используемый чаще других для нахождения параметров уравнения регрессии и известный как метод наименьших квадратов, дает наилучшие линейные несмещенные оценки. Он называется так потому, что при расчете параметров прямой линии, которая наиболее соответствует фактическим данным, с помощью этого метода стараются найти линию, минимизирующую сумму квадратов значений ошибок или расхождений между величинами Y, которые рассчитаны по уравнению прямой и обозначаются Y, и фактическими наблюдениями. Это показано на рис. 6.2. [c.265]
В случае когда Vb известны и Мп определенное (7.67), начиная с некоторого п, имеет полный ранг, наилучшая линейная оценка для в имеет вид [1171 [c.232]
В соответствии с 115] (случай коррелированных наблюдений) наилучшие линейные оценки имеют следующий вид [c.247]
Модель (7.5) является линейной моделью, подробно рассмотренной в гл. 4, 5. Если все необходимые предпосылки классической линейной регрессионной модели для (7.5) выполнены, то по МНК можно определить наилучшие линейные несмещенные оценки коэффициентов ро и р. [c.182]
Так как по предположению коэффициент р известен, то очевидно, yt, xt, ut вычисляются достаточно просто. В силу того, что случайные отклонения ut удовлетворяют предпосылкам МНК, то оценки ро и pi будут обладать свойствами наилучших линейных несмещенных оценок. [c.237]
Далее мы установим, что оценки, полученные методом наименьших квадратов, представляют собой наилучшие линейные несмещенные оценки, т. е. что в классе всех линейных несмещенных операторов оценивания оценки наименьших квадратов обладают наименьшей дисперсией. Определим произвольную линейную оценку параметра (5 как [c.29]
Доказательство только что установленного факта можно получить иным способом, взяв сразу же наилучшие линейные несмещенные оценки и показав их совпадение с оценками наименьших квадратов. Этот подход иллюстрирует метод, который будет плодотворно применяться при решении последующих задач. При тех же предположениях (2.5), что и прежде, определим. [c.30]
Итак, мы доказали, что оцека Ь метода наименьших квадратов является наилучшей линейной оценкой параметра р. Перейдем теперь к оценке еще одного параметра — дисперсии возмущений ст2. [c.95]
Замечание. Фактически теорема 2 обобщает теорему 1 в двух направлениях. Во-первых, рассматривается более общий вид ковариационной матрицы для у, а именно но эти оценки не лучше оценок (НЛНО). Мы не знаем, имеют ли они еще и меньшую дисперсию, чем обычные МНК-оценки (сравните с литературой)9. Мы знаем, что МНК-оценки обладают преимуществом простоты вычислений, поскольку при ортогональной матрице независимых переменных не нужна обратная матрица. Обращение матрицы с помощью ЭВМ может приводить к значительным ошибкам [c.300]
Простой метод наименьших квадратов для одного уравнения регрессии, т. е. мы пренебрегаем неоднородностью дисперсий и существованием более чем одного уравнения регрессии. Тогда наилучшей линейной несмещенной оценкой (НЛНО) будет простая, или обычная, оценка по методу наименьших квадратов (МНК-оценка). Регрессионные уравнения (76) в матричной записи имеют вид [c.311]
Эти оценки имеют при фиксированных значениях yit и xit нормальное распределение и являются наилучшими линейными несмещенными оценками (BLUE). [c.226]
Что такое blue оценка
Рассмотрим линейную регрессионную модель (г/, Х(3, а2 V), где /3 удовлетворяет совместным линейным ограничениям R/3 = г. Пусть V Ф 0. Тогда наилучшая линейная несмещенная оценка строго оцениваемой параметрической функции W/3 равна W/3, при этом [c.340]
Метод, используемый чаще других для нахождения параметров уравнения регрессии и известный как метод наименьших квадратов, дает наилучшие линейные несмещенные оценки. Он называется так потому, что при расчете параметров прямой линии, которая наиболее соответствует фактическим данным, с помощью этого метода стараются найти линию, минимизирующую сумму квадратов значений ошибок или расхождений между величинами Y, которые рассчитаны по уравнению прямой и обозначаются Y, и фактическими наблюдениями. Это показано на рис. 6.2. [c.265]
Модель (7.5) является линейной моделью, подробно рассмотренной в гл. 4, 5. Если все необходимые предпосылки классической линейной регрессионной модели для (7.5) выполнены, то по МНК можно определить наилучшие линейные несмещенные оценки коэффициентов ро и р. [c.182]
Так как по предположению коэффициент р известен, то очевидно, yt, xt, ut вычисляются достаточно просто. В силу того, что случайные отклонения ut удовлетворяют предпосылкам МНК, то оценки ро и pi будут обладать свойствами наилучших линейных несмещенных оценок. [c.237]
Далее мы установим, что оценки, полученные методом наименьших квадратов, представляют собой наилучшие линейные несмещенные оценки, т. е. что в классе всех линейных несмещенных операторов оценивания оценки наименьших квадратов обладают наименьшей дисперсией. Определим произвольную линейную оценку параметра (5 как [c.29]
Доказательство только что установленного факта можно получить иным способом, взяв сразу же наилучшие линейные несмещенные оценки и показав их совпадение с оценками наименьших квадратов. Этот подход иллюстрирует метод, который будет плодотворно применяться при решении последующих задач. При тех же предположениях (2.5), что и прежде, определим. [c.30]
При условии, что значения л известны, предпочтительнее оценивать b по формуле (7.26), нежели пользоваться оценкой, найденной обыкновенным методом наименьших квадратов р из (7.30), поскольку первая формула дает наилучшую линейную несмещенную оценку. По- [c.214]
Предложенный метод требует ответа на ряд вопросов. Необходимо установить, что формальная оценка b из (7.44) представляет собой наилучшую линейную несмещенную оценку вектора р из (7.42), где наилучшая относится к выборочной и предварительной информации одновременно. На первый взгляд эта задача кажется тупиковой, поскольку модель (7.42) объединяет два качественно различных типа данных, а именно выборочные наблюдения для у и X и несколько априорных значений статистических оценок, указанных в г и R. В ряде обычных прикладных ситуаций переменная Y, а следовательно, и возмущение и, измеряются в постоянных долларах, приходящихся на душу населения в год, в то время как ошибка и относится к эластичности от дохода, и следовательно, является безразмерной величиной. Однако применение обобщенного метода наименьших квадратов означает, что минимизируется взвешенная сумма квадратов [c.221]
Для некоторой заданной матрицы группировки G оценка Ь, полученная обобщенным методом наименьших квадратов (см. (7.58)), является наилучшей линейной несмещенной оценкой. Выборочные дисперсии оцененных коэффициентов необходимо оказываются больше соответствующих дисперсий для оценок, полученных методом наименьших квадратов в применении к исходным несгруппированным наблюдениям (если получение таких оценок возможно). Потеря эффективности [c.228]
Так как (uu ) = V, то из гл. 7 ясно, что обобщенный метод наименьших квадратов дает наилучшую линейную несмещенную оценку, когда матрица V известна. Обыкновенный метод наименьших квадратов приводит нас в этом случае к неэффективным оценкам и к неэффективным прогнозам. Мы вернемся к этому в параграфах 8.5 и 8.6. [c.248]
Так как дисперсионная матрица для и не является скалярной, обыкновенный метод наименьших квадратов оказывается неэффективным и наилучшая линейная несмещенная оценка вектора р достигается с помощью обобщенного метода наименьших квадратов. Если, например, известно, что возмущения формируются в рамках авторегрессионной схемы первого порядка и значение параметра р задано, то обобщенный метод [c.257]
В чем суть наилучших линейных несмещенных оценок (BLUE) [c.135]
Как отмечалось в разделе 5.1, при рассмотрении классической линейной регрессионной модели МНК дает наилучшие линейные несмещенные оценки (BLUE-оценки) лишь при выполнении ряда предпосылок, одной из которых является постоянство дисперсии отклоне- [c.212]
Оценки параметров, оставаясь линейными и несмещенными, перестают быть эффективными. Следовательно, они перестают обладать свойствами наилучших линейных несмещенных оценок (BLUE-оценок). [c.230]
Как известно, при выполнении определенных предпосылок МНК дает наилучшие линейные несмещенные оценки (BLUE-оценки). Причем свойство несмещенности и эффективности оценок остается в силе даже, если несколько коэффициентов регрессии оказываются статистически незначимыми. Однако несмещенность фактически означает лишь то, что при многократном повторении наблюдений (при постоянных объемах выборок) за исследуемыми величинами средние значения оценок стремятся к их истинным значениям. К сожалению, повторять наблюдения в одинаковых условиях в экономике практически невозможно. Поэтому это свойство ничего не гарантирует в каждом конкретном случае. Наименьшая возможная дисперсия вовсе не означает, что дисперсия оценок будет мала по сравнению с самими оценками. В ряде случаев такая дисперсия достаточно велика, чтобы оценки коэффициентов стали статистически незначимыми. [c.247]
Однако если для моделей данного типа использовать обыкновенный МНК, то оценки, получаемые с его помощью, не обладают свойствами наилучших линейных несмещенных оценок (BLUE). Поэтому для определения коэффициентов в этом случае используются другие методы. [c.268]
В случае когда n x n нормированная1 матрица ковариаций fi полностью известна, то, как было показано в разделе 5.2, наилучшая линейная несмещенная оценка (а также оценка максимального правдоподобия для J3) задается формулой (см. (5.4)) [c.160]
Мы предпочитаем оценки коэффициентов регрессии у г, которые эффективны и для которых можно проверить значимость. Оценки эффективны, если они являются наилучшими линейными несмещенными оценками (НЛНО). Термин наилучшие относится к свойству минимальности дисперсии. Оценки обобщенного МНК, будут такими оценками (НЛНО), но они требуют знания ковариационной матрицы ошибок наблюдений (2г и 2 в (2.8) и (2.17) в дополнении 2). К сожалению, нам ковариационная матрица неизвестна. Мы можем оценить элементы этой матрицы. (Ее диагональные элементы, т. е. дисперсии, оцениваются величинами sfr, обобщенный МНК для системы уравнений также требует оценивания ковариаций эти ковариации не оценивались в данном эксперименте, но они оценивались в дополнительном эксперименте.) Замена ковариационной матрицы в обобщенном методе ковариационной матрицей оценок позволяет получить несмещенные оценки 7о-> но эти оценки не лучше оценок (НЛНО). Мы не знаем, имеют ли они еще и меньшую дисперсию, чем обычные МНК-оценки (сравните с литературой)9. Мы знаем, что МНК-оценки обладают преимуществом простоты вычислений, поскольку при ортогональной матрице независимых переменных не нужна обратная матрица. Обращение матрицы с помощью ЭВМ может приводить к значительным ошибкам [c.300]
Простой метод наименьших квадратов для одного уравнения регрессии, т. е. мы пренебрегаем неоднородностью дисперсий и существованием более чем одного уравнения регрессии. Тогда наилучшей линейной несмещенной оценкой (НЛНО) будет простая, или обычная, оценка по методу наименьших квадратов (МНК-оценка). Регрессионные уравнения (76) в матричной записи имеют вид [c.311]
Эти оценки имеют при фиксированных значениях yit и xit нормальное распределение и являются наилучшими линейными несмещенными оценками (BLUE). [c.226]
Следовательно, наилучшая линейная несмещенная оценка вектора р если мы ограничены данными у и X, будет найдена применением обоб щенното метода наименьших квадратов к уравнению (7.54), так чт
Что такое blue оценка
2.3. Статистические свойства оценок метода наименьших квадратов
Поскольку полученные оценки a и b коэффициентов линейной регрессии основаны на статистических данных и являются случайными величинами, то естественно установить свойства этих оценок, как случайных величин. Более того, не выяснив этих свойств, невозможно сделать обоснованных выводов относительно качества и надежности полученных оценок. Необходимо, в частности, определить такие их статистические характеристики, как математическое ожидание и дисперсия. К желательным свойствам оценок относятся также несмещенность и состоятельность. Далее, если бы удалось определить вид распределения (плотности распределения) оценок, можно было бы построить доверительные интервалы для истинных значений параметров регрессии (то есть получить интервальные оценки коэффициентов) и реализовать процедуры проверки гипотез относительно их значений. Важную роль играет также изучение статистических свойств остатков оцененной регрессии.
Все эти задачи можно решить, основываясь на некоторых правдоподобных теоретических предпосылках (гипотезах) модели, выполнение которых на практике подлежит проверке с помощью специально разработанных для этого статистических процедур.
Предположение относительно независимых переменных
Предположения относительно случайной составляющей модели
При выполнении предпосылки относительно переменной x статистические свойства оценок параметров и зависимой переменной, а также остатков, целиком определяются вероятностными свойствами случайной составляющей регрессионной модели. Относительно случайной составляющей в классическом регрессионном анализе предполагают выполнение следующих условий, которые называются условиями Гаусса-Маркова и играют ключевую роль при изучении свойств оценок, полученных по методу наименьших квадратов.
1. Первое условие заключается в том, что математическое ожидание случайной составляющей во всех наблюдениях должно быть равно нулю. Формально это записывается так
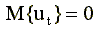 , для всех t =1,2,…,n. , для всех t =1,2,…,n. |
Смысл этого условия заключается в том, что не должно быть систематического смещения случайной составляющей. В линейной регрессии систематическое смещение линии регрессии учитывается с помощью введения параметра смещения 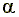
2. Дисперсия случайной составляющей постоянна для всех наблюдений (то есть не зависит от номера наблюдения). Это условие записывается так
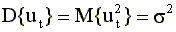 , где дисперсия , где дисперсия 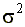 — величина постоянная. — величина постоянная. |
Это свойство дисперсии ошибок называется гомоскедастичностью (однородностью) (запомните этот термин).
Графическая иллюстрация понятий гомоскедастичность и гетероскедастичность
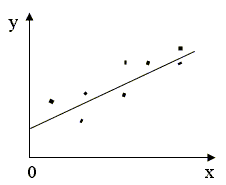
Рис. 2.6а. Гомоскедастичность
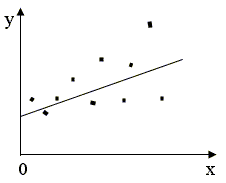
Рис. 2.6б. Гетероскедастичность
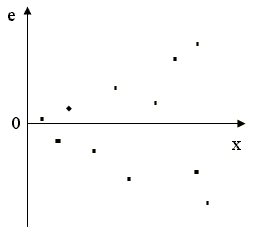
Рис. 2.6в. Гетероскедастичность
3. Случайные составляющие модели для различных наблюдений некоррелированы. Это условие записывается таким образом
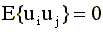 , для всех i не равных j (i, j=1,2,…,n). , для всех i не равных j (i, j=1,2,…,n). |
Выполнение этого условия означает отсутствие систематической (статистической) связи между значениями случайного члена в любых двух наблюдениях. Это свойство на практике также проверяется с помощью статистических процедур на основе анализа остатков модели. Если оно нарушается, то процедура оценки параметров должна быть скорректирована.
4. Четвертое условие Гаусса-Маркова записывается так
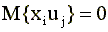 , для всех i и j, , для всех i и j, |
и означает, что объясняющие переменные и случайные составляющие некоррелированы для всех наблюдений. Ранее мы предположили, что объясняющая переменная в модели не является стохастической. В этом случае четвертое условие выполняется автоматически.
Дополнительное предположение о нормальном распределении ошибок
Данное предположение является, пожалуй, наиболее спорным. Дело в том, что предположение о нормальности можно считать правдоподобным, если значения случайной величины порождаются в результате воздействия большого количества независимых случайных факторов, каждый из которых не обязательно имеет нормальное распределение. Примером такого воздействия является так называемое броуновское движение (хаотичное движение малых частиц в жидкости как результат совокупного воздействия на частицу (ударов, соударения) большого количества молекул жидкости).
Если случайные величины в модели распределены по нормальному закону, то из свойств некоррелированности в третьем и четвертом условиях Гаусса-Маркова следует и независимость соответствующих случайных величин.
2.3.2. Свойства выборочных вариаций и ковариаций. Остаточные ошибки (остатки) модели, их свойства
Свойства выборочных вариаций (дисперсий) и ковариаций
Для дальнейшего изложения нам понадобиться установить ряд правил, которые можно использовать при преобразовании выражений, содержащих выборочные вариации и ковариации.
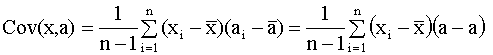 , , |
откуда следует свойство
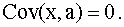
Далее, нетрудно видеть, что имеют место равенства
Системы одновременных уравнений (СОУ) в эконометрике



Гетероскедастичность, мультиколлинеарность и автокорреляция
Предпосылки метода наименьших квадратов (МНК) теорема Гаусса-Маркова
Качественный анализ эконометрических моделей (значимость, достоверность)
Множественные эконометрические модели и проблемы их построения
Множественные эконометрические модели и качественный их анализ
Лекция 3
Количесвенная зависимость финансово-экономических показателей от двух и более факторных (экзогенных) показателей описываются многофакторной корреляционно-регрессионной моделью
y – зависимый показатель;
x – независимый показатель.
Чаще всего применяются линейные многофакторные модели:
Параболическая множественная модель:
С помощью компьютера часто строят так называемые полиномы высоких степеней.
Проблемы построения множественных моделей:
— проблема выбора основных факторных показателей существенно влияющих на результат
— число факторов может оказаться очень большим, но эконометрическая модель с большим набором факторных показателей, как правило, не качественная.
Обычно 4-ех и 5-ти факторные показатели и т.д. только ухудшают качественные характеристики эконометрической модели.
Например, если вы взяли 2 самых значимых фактора больше всего влияющих на y, но связь между этими показателями очень высокая коэффициент корреляции = 0,9 и выше, модель уже будет не качественной. Связь должна быть не больше 0,8.
Общие требования к исходным данным:
1. Они должны быть репрезентативны
2. Они должны состоять из вероятностно независимых результатов наблюдения
3. Они должны быть однородными
4. Они должны иметь нормальное или близкое к нормальному распределение
Корреляционно-регрессионные модели дают результаты как правило отличающихся от фактических значений результирующего финансово-экономического показателя y, ŷ это происходит:
— Из-за наличия случайных одномоментных не учтенных непредсказуемых факторов
— невозможно охватить всю совокупность данных по показателю
Для анализа качества эконометрической модели оценивают достоверность, значимость с помощью целого ряда показателей, характеристик, оценок.
Основные характеристики достоверности:
1. Среднеквадратическая ошибка (отклонение)
k – число параметров, экзогенных переменных.
Чем меньше отклонение, тем значение точнее.
2. Среднеквадратическое отклонение (дисперсия) – разброс значений.
В хорошей модели среднеквадратическое отклонение должно быть > среднеквадратической ошибки.
3. Расчет коэффициента корреляции.
Корреляция – теснота связи между показателями.
R=-1 обратная зависимость
В уравнениях множественной регрессии можно рассчитать как коэффициент множественной корреляции и коэффициент множественной детерминации.
В то же время можно рассчитать коэффициенты частной корреляции, показывающие влияние каждого отдельного факторного независимого показателя на зависимый с учетом остальных.
4. Проверка нулевой гипотезы о равенстве 0-коэффициента регрессии по критерию Стьюдента.
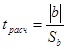
где
Табличный критерий Стьюдента приводится для степени свободы 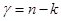
5. Расчет доверительного интервала коэффициента регрессии.
6. Проверка нулевой гипотезы о равенстве о-коэффициента корреляции по критерию Стьюдента.
Ошибка выборочного коэффициента корреляции (среднеквадратическая ошибка) для парной регрессии.
Для множественной регрессии
Для множественной
7. Доверительный интервал для коэффициента множественной регрессии.
8. Проверка значимости корреляционно-регрессионного уравнения по F-критерию Фишера.
Для степеней свободы 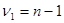
где
Условия качественной эконометрической модели (или предпосылки МНК, или условия Гаусса-Маркова):
1.Математическое ожидание случайного отклонения (Ɛi) равно 0 для всех наблюдений:
Математическое ожидание – среднее ожидаемое значение случайной величины и приблизительно равно среднему значению y.
2.Дисперсия случайных отклонений постоянна для любых наблюдений i и j:
Т.е. должна обеспечиваться гомоскедастичность.
Гомоскедастичность – это постоянство дисперсии отклонений или независимость дисперсии от № наблюдения.
Дисперсия – разброс ошибок.
Гетероскедастичность – непостоянство дисперсии отклонений или зависимость от № наблюдения. Требует анализа и устранения.
3.Случайные отклонения (ошибки) Ɛi и Ɛj являются независимыми друг от друга:
Теснота связи между 1-ой и 2-ой ошибкой должна быть близка к 0. Другими словами, должна отсутствовать автокорреляция ошибок (отклонений).
4.Случайное отклонение Ɛi должно быть независимо от факторной или экзогенной переменной xi:
5.Модель является линейной относительно параметров.
Если предпосылки 1 – 5 выполнены, тогда оценки:
1) являются несмещенными (т.е. коэффициенты регрессии точно устанавливают положение прямой или уравнение регрессии);
2) являются состоятельными (т.е. при увеличении объема выборки, точность уравнения регрессии должна и будет возрастать);
3) являются эффективными (т.е. имеют наименьшую дисперсию по сравнению с любыми другими).
В зарубежной эконометрике эти оценки называют оценками BLUE:
Best – наилучшие;
Linear – линейные;
Unbiased – не совмещенные;
Estimators – оценки.
Автокорреляция – это корреляционная связь или степень тесноты связи между последовательными наблюдениями временного ряда или пространственной выборки (y) или отклонениями (ошибками).
Качественная эконометрическая модель не должна характеризоваться высокой автокорреляцией как значения показателя, так и ошибок.
Коэффициент автокорреляции первого порядка для отклонений (ошибок):
На практике анализ автокорреляции ошибок ведут по статистике Дарбина-Уотсона: