Что такое абстрактная модель
Абстрактные (нематериальные) модели
Абстрактные модели нельзя потрогать, они не имеют вещественного воплощения.
Основу таких моделей составляет информация, а такой тип моделирования реализует теоретический метод познания окружающей действительности. Основанием для дальнейшей классификации абстрактных моделей выберем возможность их реализации и исследования при помощи компьютера. По этому признаку выделяются следующие подклассы:
Мысленные модели формируются в воображении человека в результате раздумий, умозаключений, иногда в виде некоторого образа. Примером мысленной модели является модель поведения при переходе через дорогу. Человек анализирует ситуацию на дороге (какой сигнал подает светофор, как далеко находятся машины, с какой скоростью они движутся и т. п.) и вырабатывает модель поведения. Если ситуация смоделирована правильно, то переход будет безопасным, если нет, то может произойти дорожно-транспортное происшествие. Такие модели сопутствуют любой сознательной деятельности человека. Собираясь делать покупки, человек мысленно представляет, что и сколько можно купить на имеющуюся у него сумму. Ожидая транспорт на остановке, прикидывает, как быстрее добраться до нужного места.
К моделям такого типа можно отнести и идею, возникшую у изобретателя, и музыкальную тему, промелькнувшую в мыслях у композитора, и рифму, родившуюся в голове поэта. Во всех приведенных примерах модели предшествовали созданию объекта (нового устройства, музыкального произведения, стихотворения), являлись одним из этапов творческого процесса. Подобные модели могут возникнуть у зрителя, слушателя, читателя как реакция на уже существующие объекты (музыку, картину, поэму). Мысленная модель может быть выражена в разговорной форме. В этом случае она часто называется вербальной (от лат. verbalis — устный). Вербальную модель человек использует для передачи своих мыслей другим.
Образы, возникающие у разных людей как реакция на одни и те же объекты и явления, могут сильно различаться. Поэтому образная модель очень индивидуальна и не отображает прототип с достаточной степенью достоверности. Невозможно получить впечатление от музыкального произведения, услышав не музыку, а рассказ о ней.
Чтобы информацию можно было использовать для обработки на компьютере, необходимо выразить ее при помощи системы знаков. Кроме того, информацию необходимо представить в такой форме, которая бы отвечала поставленной цели исследования. Такую работу называют формализацией задачи.
Поэтому наряду с вербальными и мысленными моделями используются более строгие — информационные модели.
Формализация – замена реального объекта его информационной моделью.
Существуют разнообразные системы условных обозначений и соглашений, относящихся к разным областям деятельности и пригодных для описания моделей. Подобную систему и правила использования ее элементов называют языком. Язык может быть разговорным, алгоритмическим, математическим, языком кодирования и пр. Информация, характеризующая объект или процесс, может иметь разную форму представления, выражаться различными средствами. По степени формализации, строгости описания это многообразие можно условно разделить на образно-знаковые и знаковые модели(см. рис.5). Рис. 5
Ярким примером образно-знаковой модели является географическая карта. Цвет и форма материков, океанов, гор, изображенных на карте, сразу подключает образное мышление. По цвету на карте можно сразу оценить рельеф. Например, с голубым цветом у человека ассоциируется вода, с зеленым — цветущий луг, равнина. Карта изобилует условными обозначениями. Зная этот язык, человек может получить достоверную информацию об интересующем его объекте. Информационная модель в этом случае будет результатом осмысления сведений, полученных при помощи органов чувств и информации, закодированной в виде условных изображений.
Еще один пример такой модели — фотография. Фотоаппарат позволяет получить изображение оригинала. Обычно фотография дает нам довольно точное представление о внешнем облике человека. Существуют некоторые признаки (высота лба, посадка глаз, форма подбородка), по которым специалисты могут определить характер человека, его склонность к тем или иным поступкам. Этот специальный язык формируется из сведений, накопленных в области физиогномики и собственного опыта. Задавшись разными целями, по одной и той же фотографии можно получить различные информационные модели. Они будут результатом обработки образной информации, полученной при разглядывании фотографии, и информации, сложившейся на основе знания специального профессионального языка.
По форме представления образно-знаковых моделей среди них можно выделить следующие группы:
Знаковые модели можно разделить на следующие группы:
Абстрактные модели и их классификация
Данная презентация расчитана на учеников 11 класса для углубленного изучения по учебнику Полякова.
Просмотр содержимого документа
«Абстрактные модели и их классификация»
Абстрактные модели и их классификация
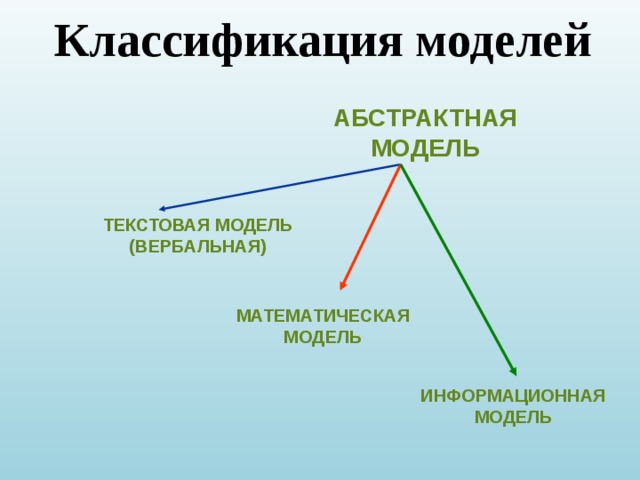
это модель, отражающая лишь самые общие характеристики моделируемого явления. Чаще всего абстрактная модель даёт лишь качественные характеристики моделируемого объекта или явления.
Текстовая (вербальная) модель
Использует последовательности предложений на формализованных диалектах естественного языка для описания объекта в той или иной предметной области:
ВЕРБАЛЬНЫЕ МОДЕЛИ СОЗДАЮТСЯ ДЛЯ:
ВЕРБАЛЬНЫЕ МОДЕЛИ СОЗДАЮТСЯ ДЛЯ:
выражает существенные черты объекта или процесса языком уравнений и других математических форм:
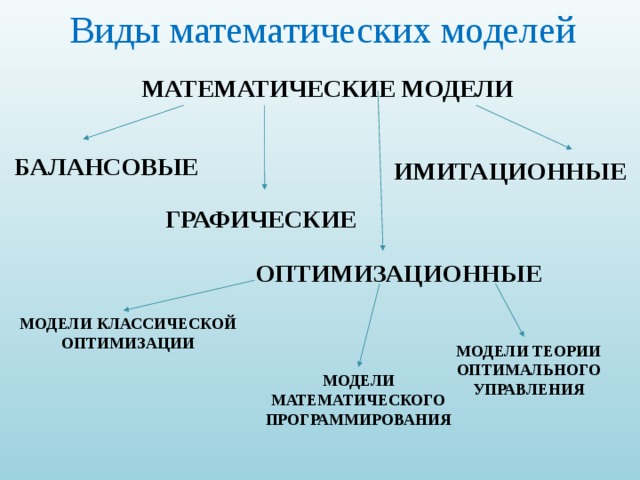
Виды математических моделей
МОДЕЛИ КЛАССИЧЕСКОЙ ОПТИМИЗАЦИИ
МОДЕЛИ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
МОДЕЛИ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
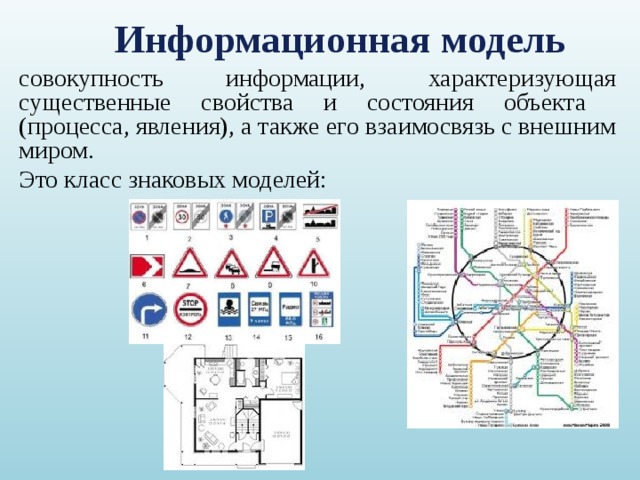
совокупность информации, характеризующая существенные свойства и состояния объекта (процесса, явления), а также его взаимосвязь с внешним миром.
Это класс знаковых моделей:
ВИДЫ ИНФОРМАЦИОННЫХ МОДЕЛЕЙ
в прикладных науках
Абстрактная модель
Абстрактная модель [abstract model] — см. Концептуальная модель
Смотреть что такое «Абстрактная модель» в других словарях:
Абстрактная модель — Абстрактная модель это модель, отражающая лишь самые общие характеристики моделируемого явления. Чаще всего абстрактная модель дает лишь качественные характеристики моделируемого объекта или явления. Сферы применения абстрактных моделей… … Википедия
МОДЕЛЬ — абстрактное или вещественное отображение объектов или процессов, адекватное исследуемым объектам (процессам) в отношении некоторых заданных критериев. Напр., математическая модель слоенакопления (абстрактная модель процесса), блок диаграмма… … Геологическая энциклопедия
Модель — У этого термина существуют и другие значения, см. Модель (значения). Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторите … Википедия
абстрактная синтаксическая нотация 1-й версии — [ГОСТ Р 54325 2011 (IEC/TS 61850 2:2003)] абстрактно синтаксическая нотация версии один — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] абстрактная синтаксическая нотация номер один Система… … Справочник технического переводчика
Модель Колба — теория специалиста по психологии обучения взрослых Дэвида Колба, посвященная поэтапному формированию умственных действий. Она в различных вариациях широко применяется в ходе интерактивных уроков. Теория обучения Колба содержит четыре основных… … Википедия
Абстрактная Грамматика Поведения Осгуда — Абстрактная грамматика поведения (abstract performance grammar) Ч. Осгуда семантико компонентная модель, созданная в рамках репрезентативного необихевиоризма, основанная на положении, что когнитивные структуры, обеспечивающие интерпретацию… … Психологический словарь
Модель OSI — Сетевая модель OSI (базовая эталонная модель взаимодействия открытых систем, англ. Open Systems Interconnection Basic Reference Model) абстрактная сетевая модель для коммуникаций и разработки сетевых протоколов. Представляет уровневый подход к… … Википедия
Модель вычислений — Иные значения см. разделе в Компьютерное моделирование. Теория вычислимости и теория сложности вычислений трактует модель вычисления (англ. model of computation) не только как определение множества допустимых операций, использованных для… … Википедия
МОДЕЛЬ ВЫЧИСЛИТЕЛЬНАЯ — типовая абстрактная или конкретная задача, соответствующая проблеме численного решения нек рого класса математич. или прикладных задач. Напр., в теории квадратур рассматривают задачу вычисления интегралов от функций, удовлетворяющих нек рому… … Математическая энциклопедия
Классификация абстрактных моделей
К классификации абстрактных моделей можно подходить с разных позиций, положив в основу классификации различные принципы. Можно классифицировать модели по отраслям наук (математические модели в физике, биологии, социологии и т.д.) и по применяемому логико-математическому аппарату (модели, основанные на использовании логик: формальной, математической, булевой, модальной, нечеткой; численно-математичесих методов: обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, стохастических методов, дискретных алгебраических преобразований и т.д.). Далее, если поинтересоваться общими закономерностями моделирования в разных науках (безотносительно к логико-математическому аппарату) и поставить на первое место цели моделирования, то можно прийти к следующей классификации:
Остановимся на этой классификации подробнее и поясним ее на примерах.
Моделируя движение кометы, вторгшейся в Солнечную систему, мы описываем ситуацию (предсказываем траекторию полета кометы, расстояние, на котором она пройдет от Земли и т.д.), т.е. ставим чисто описательные цели. У нас нет никаких возможностей повлиять на движение кометы, что-то изменить в процессе моделирования.
В оптимизационных моделях мы можем воздействовать на процессы, пытаясь добиться какой-то цели. В этом случае в модель входит один или несколько параметров, доступных нашему влиянию. Например, меняя тепловой режим в зернохранилище, мы можем стремиться подобрать такой, чтобы достичь максимальной сохранности зерна, т. е. оптимизируем процесс.
Часто приходится оптимизировать процесс по нескольким параметрам сразу, причем цели могут быть весьма противоречивыми. Например, зная цены на продукты и потребность человека в пище, организовать питание больших групп людей (в армии, летнем лагере и др.) как можно полезнее и как можно дешевле. Ясно, что эти цели, вообще говоря, совсем не совпадают, т.е. при моделировании будет несколько критериев, между которыми надо искать баланс. В этом случае говорят о многокритериальных моделях.
Игровые модели могут иметь отношение не только к детским играм (в том числе и компьютерным), но и к вещам весьма серьезным. Например, полководец перед сражением в условиях наличия неполной информации о противостоящей армии должен разработать план, в каком порядке вводить в бой те или иные части и т.п., учитывая возможную реакцию противника. В современной математике есть специальный раздел – теория игр, изучающий методы принятия решений в условиях неполной информации.
Наконец, бывает, что модель в большой мере подражает реальному процессу, т.е. имитирует его. Например, моделируя динамику численности микроорганизмов в колонии, можно рассматривать совокупность отдельных объектов и следить за судьбой каждого из них, ставя определенные условия для его выживания, размножения и т.д. При этом часто явное численно-математическое описание процесса не используется, а используются некоторые логические условия, характеризующие поведение элементов моделируемой системы (например, по истечении некоторого отрезка времени микроорганизм делится на две части, а другого отрезка – погибает). Другой пример – моделирование движения молекул в газе, когда каждая молекула представляется в виде шарика, и задаются условия поведения этих шариков при столкновении друг с другом и со стенками (например, абсолютно упругий удар); при этом не нужно использовать никаких уравнений движения.
Можно сказать, что чаще всего имитационное моделирование применяется в попытке описать свойства большой системы при условии, что поведение составляющих ее объектов очень просто и логически четко сформулировано. Численно-математическое описание тогда производится на уровне статистической обработки результатов моделирования при нахождении макроскопических характеристик системы. Такой компьютерный эксперимент фактически претендует на воспроизведение натурного эксперимента. На вопрос же «зачем это делать?» можно дать следующий ответ: имитационное моделирование позволяет выделить «в чистом виде» следствия гипотез, заложенных в наши представления о микрособытиях, очистив их от неизбежного в натурном эксперименте влияния других факторов, о которых мы можем даже не подозревать. Если же такое моделирование включает и элементы математического описания событий на микроуровне, и если исследователь при этом не ставит задачу поиска стратегии регулирования результатов (например, управления численностью колонии микроорганизмов), то отличие имитационной модели от дескриптивной достаточно условно; это, скорее, вопрос терминологии.
Еще один подход к классификации абстрактныхх моделей подразделяет их на детерминированные и стохастические (вероятностные). В детерминированных моделях входные параметры поддаются измерению однозначно и с любой степенью точности, т.е. являются детерминированными величинами. Соответственно, процесс эволюции такой системы детерминирован. В стохастических моделях значения входных параметров известны лишь с определенной степенью вероятности, т.е. эти параметры являются стохастическими; соответственно, случайным будет и процесс эволюции системы. При этом, выходные параметры стохастической модели могут быть как величинами вероятностными, так и однозначно определяемыми.
Наконец, если ограничиться непрерывными детерминистскими моделями, то их часто подразделяют на системы с сосредоточенными параметрами и системы с распределенными параметрами. Системы с сосредоточенными параметрами описываются с помощью конечного числа обыкновенных дифференциальных уравнений для зависящих от времени переменных. Пространство состояний имеет здесь конечную размерность (число степеней свободы системы конечно). В противоположность этому под системами с распределенными параметрами понимают системы, описываемые конечным числом дифференциальных уравнений в частных производных. Здесь переменные состояния в каждый момент времени есть функции одной или нескольких пространственных переменных. Пространство состояний имеет в этом случае бесконечную размерность, т.е. система обладает бесконечным числом степеней свободы.
Подчеркнем, что граница между вербальными, математическими и информационными моделями может быть проведена весьма условно. Так, информационные модели иногда считают подклассом математических моделей. Однако, в рамках информатики как самостоятельной науки, отделенной от математики, физики, лингвистики и других наук, выделение информационных моделей в отдельный класс является целесообразным.
Отметим, что существуют и иные подходы к классификации абстрактных моделей; общепринятая точка зрения здесь еще не установилась.
В прикладных науках различают следующие виды абстрактных моделей:
Иерархия моделей
Модели могут быть классифицированы по иерархическому признаку моделируемых систем. По мере сложности их информационных потоков целевые системы и их модели можно разделить на следующие уровни.
Основные принципы моделирования
Основные принципы моделирования состоят в следующем:
Научная электронная библиотека
Оразбаев Б. Б., Курмангазиева Л. Т., Коданова Ш. К.,
3.3. Теория систем. Методы и модели теории систем
1. Определение понятия модель и моделирование.
2. Назначение моделей. Классификация моделей.
3. Уровни моделирования.
1. Определение понятия модель и моделирование
Теория систем – научная и методологическая концепция исследования объектов, представляющих собой системы.
Теория систем – междисциплинарная область науки, рассматривающая поведение и взаимодействие различных систем в природе, обществе и науке. Основной целью теории систем является обнаружение основных принципов функционирования систем, необходимых для описания любой группы взаимодействующих объектов, во всех областях исследований, как правило с помощью моделей и моделирования.
Первоначально моделью называли некое вспомогательное средство, объект, который в определённой ситуации заменял другой объект.
При этом далеко не сразу была понята универсальность законов природы, всеобщность моделирования, т.е. не просто возможность, но и необходимость представлять любые наши знания в виде моделей. Например, древние философы считали невозможным моделирование естественных процессов, так как, по их представлениям, природные и искусственные процессы подчинялись различным закономерностям. Они полагали, что отобразить природу можно только с помощью логики, методов рассуждений, споров, т.е., по современной терминологии, языковых (дескриптивных) моделей. Через несколько столетий девизом английского Королевского научного общества стал лозунг «Ничего словами!», который явился кратчайшим изложением принципов естествознания: признавались только выводы, подкреплённые экспериментально или математическими выкладками. В английском языке до сих пор в понятие «наука» не входят области знания, которым в русском языке соответствует термин «гуманитарные науки», – они отнесены к категории «искусств».
В результате очень долго понятие «модель» относилось только к материальным объектам специального типа, например манекен (модель человеческой фигуры), гидродинамическая уменьшенная модель плотины, модели судов и самолетов, чучела (модели животных) и т.п.
Осмысливание основных особенностей таких моделей привело к разработке многочисленных определений, типичным призером которых служит следующее: моделью называется некий объект-заместитель, который в определённых условиях может заменять объект-оригинал, воспроизводя интересующие нас свойства и характеристики оригинала, причём имеет существенные преимущества удобства (наглядность, обозримость, доступность испытаний, лёгкость оперирования с ним и пр.).
Затем были осознаны модельные свойства чертежей, рисунков, карт – реальных объектов искусственного происхождения, воплощающих абстракцию довольно высокого уровня.
Следующий шаг заключался в признании того, что моделями могут служить не только реальные объекты, но и абстрактные, идеальные построения. Типичным примером служат математические модели. В результате деятельности математиков, логиков и философов, занимавшихся исследованием оснований математики, была создана теория моделей. В ней модель определяется как результат отображения одной абстрактной математической структуры на другую, также абстрактную, либо как результат интерпретации первой модели в терминах и образах второй.
В XX в. понятие модели становится всё более общим, охватывающим и реальные, и идеальные модели. При этом понятие абстрактной модели вышло за пределы математических моделей, стало относиться к любым знаниям и представлениям о мире.
Следует отметить, что споры вокруг такого широкого толкования понятия модели продолжаются и поныне. Рассмотрим аргументы, фигурирующие в таких спорах. Стоит ли понятие абстрактной модели распространять на такие формы научных знаний, как законы, гипотезы, теории? Сторонники положительного ответа на этот вопрос отмечают, что психологический барьер неприятия объясняется тем, что понятия гипотезы, закономерности, теории сформировались и установились в языке науки и философии значительно раньше, чем понятие модели. Эти понятия, будучи исторически первыми, воспринимаются и как логически первичные, причём в этой схеме модели отводится роль лишь вспомогательного средства. Однако при этом содержание понятия модели неоправданно сужается. Модели могут быть качественно различными, они образуют иерархию, в которой модель более высокого уровня (например, теория) содержит модели нижних уровней (скажем, гипотезы) как свои части, элементы. Другой вопрос, часто возникающий в спорах: не означает ли такое широкое толкование модели, что это понятие становится применимым ко всему и, следовательно, логически пустым? Этот вопрос даёт возможность обсудить некоторые особенности моделей.
Во-первых, ещё раз отметим иерархичность моделей, поэтому применительно к разным объектам понятие модели может иметь разное содержание.
Во-вторых, тот факт, что любой объект может быть использован как модель, вовсе не означает, что он не может быть ничем иным. Например, ботинок также может являться моделью его владельца (скажем, по запаху ботинка сыскная собака отыщет преследуемого; по состоянию ботинка можно судить о некоторых особенностях сложения и даже чертах характера его хозяина), но это не лишает смысла ни понятие «обувь», ни понятие «модель».
В-третьих, самые общие понятия совсем не являются логически пустыми: материя, движение, энергия, организация, система, модель.
Модель есть способ существования знаний.
В широком смысле под моделированием следует понимать процесс адекватного отображения с помощью модели наиболее существенных сторон исследуемого объекта или явления с точностью, которая необходима для практических нужд.
В общем случае моделированием можно назвать также особую форму опосредствования, основой которого является формализованный подход к исследованию сложной системы.
Теоретической базой моделирования является теория подобия. Подобие – это взаимно однозначное соответствие между двумя объектами, при котором известны функции перехода от параметров одного объекта к параметрам другого, а математические описания этих объектов могут быть преобразованы в тождественные. Теория подобия даёт возможность установить наличие подобия или позволяет разработать способ его получения.
Таким образом, моделирование – это процесс представления объекта исследования адекватной (подобной) ему моделью и проведения экспериментов с моделью для получения информации об объекте исследования. При моделировании модель выступает и как средство, и как объект исследований, находящийся в отношении подобия к моделируемому объекту.
Иными словами, модель – это физическая или информационная система, представляющая собой объект исследования адекватно целям исследования.
2. Назначение моделей. Классификация моделей
Всякий процесс труда есть деятельность, направленная на достижение определённой цели. Целевой характер имеет любая деятельность человека, она всегда целесообразна, целенаправленна.
Важнейшим организующим элементом деятельности является цель – образ желаемого будущего, т.е. модель состояния, на реализацию которого направлена деятельность.
Однако роль моделирования этим не ограничивается. Системность деятельности проявляется в том, что она осуществляется по определённому плану, или, как чаще говорят, по алгоритму. То есть алгоритм – образ будущей деятельности, её модель. В алгоритме моделируются все возможные ситуации, в зависимости от различных промежуточных значений параметров; возможные шаги деятельности не выполняются реально, а проигрываются на модели.
Моделирование возникает в таких сферах человеческой деятельности, как познание, общение, практическая деятельность.
Человека (субъекта моделирования) могут интересовать: внешний вид, структура, поведение объекта моделирования.
Цели и задачи моделирования влияют на выбор одного из этих трёх аспектов. Каждый аспект моделирования раскрывается через совокупность свойств.
Так, описание внешнего вида объекта сводится к перечислению его признаков. В языке эти признаки часто выражаются прилагательными: красивый, жёлтый, круглый, длинный и т.п.
Описание структуры обычно сводится к перечислению составных элементов объекта и указанию связи между ними. В языке эти элементы и связи часто выражаются именами существительными: электрон, протон, нейтрон, сила притяжения, энергетический уровень (при описании атома).
Некоторые свойства можно охарактеризовать величинами, принимающими числовые значения. Например, единицами массы, длины, мощности и пр. В этом случае они называются параметрами.
Как правило, моделирование внешнего вида объекта необходимо для идентификации (узнавания) объекта (создание фоторобота преступника), долговременного хранения (фотография, портрет).
Моделирование структуры объекта необходимо для её наглядного представления, изучения свойств объекта, выявления значимых связей, изучения стабильности объекта и пр.
Поведением объекта назовем изменения, происходящие с ним с течением времени.
Моделирование поведения необходимо для: прогнозирования, установления связей с другими объектами, управления, конструирования технических устройств и пр.
Классификация моделей. Множественность моделей одного объекта обусловлена в частности тем, что для разных целей требуется строить (использовать) разные модели.
Одним из оснований классификации моделей может быть соотнесение типов моделей с типами целей. Например, модели можно разделить на познавательные и прагматические.
Познавательные модели являются формой организации и представления знаний, средством соединения новых знаний с имеющимися. Поэтому при обнаружении расхождения между моделью и реальностью встаёт задача устранения этого расхождения с помощью изменения модели путём приближения модели к реальности.
Прагматические модели являются средством управления, средством организации практических действий, способом представления образцово правильных действий или их результата. Поэтому при обнаружении расхождения между моделью и реальностью встает задача устранения этого расхождения с помощью изменения реальности так, чтобы приблизить её к модели.
Таким образом, прагматические модели носят нормативный характер, играют роль стандарта, образца, под которые «подгоняются» как сама деятельность, так и её результат.
Примерами прагматических моделей могут служить планы, программы действий, уставы организаций, кодексы законов, алгоритмы, рабочие чертежи и шаблоны, параметры отбора, технологические допуски, экзаменационные требования и т.п.
Различают физические и абстрактные модели.
Физические модели образуются из совокупности материальных объектов. Для их построения используются различные физические свойства объектов, причём природа применяемых в модели материальных элементов не обязательно та же, что и в исследуемом объекте. Примером физической модели является макет.
Информационная (абстрактная) модель – это описание объекта исследований на каком-либо языке. Абстрактность модели проявляется в том, что её компонентами являются понятия, а не физические элементы (например, словесные описания, чертежи, схемы, графики, таблицы, алгоритмы или программы, математические описания).
Информационные модели описывают поведение объекта-оригинала, но не копируют его. Информационная модель – это целенаправленно отобранная информация об объекте, которая отражает наиболее существенные для исследователя свойства этого объекта.
Среди информационных (абстрактных) моделей различают:
– дескриптивные, наглядные и смешанные;
– гносеологические, инфологические, кибернетические, сенсуальные (чувственные), концептуальные, математические.
Гносеологические модели направлены на изучение объективных законов природы (например, модели солнечной системы, биосферы, мирового океана, катастрофических явлений природы).
Сенсуальные модели – модели каких-то чувств, эмоций, либо модели, оказывающие воздействие на чувства человека (например, музыка, живопись, поэзия).
Концептуальная модель – это абстрактная модель, выявляющая причинно-следственные связи, присущие исследуемому объекту и существенные в рамках определённого исследования. Основное назначение концептуальной модели – выявление набора причинно-следственных связей, учёт которых необходим для получения требуемых результатов. Один и тот же объект может представляться различными концептуальными моделями, которые строятся в зависимости от цели исследования. Так, одна концептуальная модель может отображать временные аспекты функционирования системы, иная – влияние отказов на работоспособность системы.
Математическая модель – абстрактная модель, представленная на языке математических отношений. Она имеет форму функциональных зависимостей между параметрами, учитываемыми соответствующей концептуальной моделью. Эти зависимости конкретизируют причинно-следственные связи, выявленные в концептуальной модели, и характеризуют их количественно.
Таким образом, модель – это специальный объект, в некоторых отношениях замещающий оригинал. Принципиально не существует модели, которая была бы полным эквивалентом оригинала. Любая модель отражает лишь некоторые стороны оригинала. Поэтому с целью получения больших зияний об оригинале приходится пользоваться совокупностью моделей.
3. Уровни моделирования
В настоящее время при анализе и синтезе сложных систем получил развитие системный подход, который отличается от классического (или индуктивного) подхода. Согласно последнему, система рассматривается с позиций перехода от частного к общему и синтезирует (конструирует) систему путём слияния её элементов, разрабатываемых раздельно.
Системный подход предполагает последовательный переход от общего к частному, когда в основе рассмотрения лежит цель, причём исследуемый объект выделяется из окружающей среды.
Системный подход позволяет решить проблему построения сложной системы с учётом всех факторов и возможностей, пропорциональных их значимости, на всех этапах исследования системы и построения её модели. Системный подход означает, что каждая система является интегрированным целым даже тогда, когда она состоит из отдельных разобщённых подсистем. Таким образом, в основе системного подхода лежит рассмотрение системы как интегрированного целого, причём это рассмотрение при разработке начинается с главного: формулировки цели функционирования.
Построение модели системы относится к числу системных задач, при решении которых синтезируют решения на базе огромного числа исходных данных. Использование системного подхода в этих условиях позволяет не только построить модель реального объекта, но и на базе этой модели выбрать необходимое количество управляющей информации в реальной системе, оценить показатели её функционирования и тем самым на базе моделирования найти наиболее эффективный вариант построения и оптимальный режим функционирования реальной системы.
В соответствии с системным подходом в процессе автоматизированного проектирования сложных систем моделирование их элементов и функциональных узлов выполняется в несколько этапов, на различных уровнях, соответствующих определённым уровням проектирования.
Методика моделирования непосредственно зависит от уровня моделирования, т.е. от степени детализации описания объекта.
Каждому уровню моделирования ставится в соответствие определённое понятие системы, элемента системы, закона функционирования элементов системы в целом и внешних воздействий.
В зависимости от степени детализации описания сложных систем и их элементов можно выделить три основных уровня моделирования.
1. Уровень структурного или имитационного моделирования сложных систем с использованием их алгоритмических моделей (моделирующих алгоритмов) и применением специализированных языков моделирования, теорий множеств, алгоритмов, формальных грамматик, графов, массового обслуживания, статистического моделирования.
2. Уровень логического моделирования функциональных схем элементов и узлов сложных систем, модели которых представляются в виде уравнений непосредственных связей (логических уравнений) и строятся с применением аппарата двухзначной или многозначной алгебры логики, нечеткой логики.
3. Уровень количественного моделирования (анализа) принципиальных схем элементов сложных систем, модели которых представляются в виде систем нелинейных алгебраических, или интегро-дифференциальных уравнений и исследуются с применением методов функционального анализа, теории дифференциальных уравнений, математической статистики.
На структурном уровне моделируется состав элементов объекта на низшем уровне структурирования. К структурным относятся бинарные отношения иерархической подчинённости, отношения порядка, смежности, сопряжённости, функциональной связи.
Так, на структурном уровне моделируются ранние этапы проектирования объекта, когда топологической моделью объекта служит ориентированный граф (орграф) C(V, E), составление которого базируется на содержательном описании состава (множество вершин V) и способа действия объекта (множество ребер Е). Вершинами орграфа vi (элементами объекта) являются, как правило, функционально законченные блоки (части) объекта, а ребрами ej – информационные связи между ними.
На логическом уровне моделирования каждому множеству, булевой матрице бинарных отношений или структурному графу соответствуют наборы логических отношений между входящими в них элементами, представленными в виде логических переменных. Множествам V и E(V) также соответствуют определённые логические отношения, отражающие причинно-следственные связи. Последние описывают последовательности изменения состояний объекта с учётом состояния других, необязательно смежных с ним, объектов.
На каждом из основных уровней моделирования возможны описания объекта с различной степенью полноты и обобщения, так как существуют разные степени детализации структурных, логических и количественных свойств и отношений. Однако задача построения требуемой приближённой модели, которая бы достаточно точно отражала характерные свойства
объекта или его элемента на данном уровне проектирования и в то же время являлась доступной для исследования, представляет значительные трудности.
Заключение. В данном параграфе изложена основа теории систем. Дано определение понятия модель и моделирование. Рассмотрена теоретическая база моделирования. Изучено назначение моделей. Дана классификация моделей: информационная модель; гносеологические модели; инфологическая модель; сенсуальные модели; концептуальная модель; математическая модель. Изучены уровни моделирования: уровень структурного или имитационного моделирования; уровень логического моделирования; уровень количественного моделирования.
2. Определение понятия модель и моделирование.
3. Теоретическая база моделирования.
4. Назначение моделей.
5. Классификация моделей.
6. Информационная модель. Гносеологические модели.
7. Инфологическая модель. Сенсуальные модели.
8. Концептуальная модель. Математическая модель.
9. Уровни моделирования.
10. Уровень структурного или имитационного моделирования.