Что такое абсолютное значение
Абсолютные и относительные статистические величины
Понятие абсолютных величин
Абсолютные величины — это результаты статистических наблюдений. В статистике в отличие от математики все абсолютные величины имеют размерность (единицу измерения), а также могут быть положительными и отрицательными.
Единицы измерения абсолютных величин отражают свойства единиц статистической совокупности и могут быть простыми, отражая 1 свойство (например, масса груза измеряется в тоннах) или сложными, отражая несколько взаимосвязанных свойств (например, тонно-километр или киловатт-час).
Единицы измерения абсолютных величин могут быть 3 видов:
Абсолютные величины могут быть моментными или интервальными. Моментные абсолютные величины показывают уровень изучаемого явления или процесса на определенный момент времени или дату (например, количество денег в кармане или стоимость основных фондов на первое число месяца). Интервальные абсолютные величины — это итоговый накопленный результат за определенный период (интервал) времени (например, зарплата за месяц, квартал или год). Интервальные абсолютные величины, в отличие от моментных, допускают последующее суммирование.
Абсолютная статистическая величина обозначается X, а их общее число в статистической совокупности — N.
Количество величин с одинаковым значением признака обозначается f и называется частота (повторяемость, встречаемость).
Cами по себе абсолютные статистические величины не дают полного представления об изучаемом явлении, так как не показывают его динамику, структуру, соотношение между частями. Для этих целей служат относительные статистические величины.
Понятие и виды относительных величин
Относительная статистическая величина — это результат соотношения двух абсолютных статистических величин.
Если соотносятся абсолютные величины с одинаковой размерностью, то получаемая относительная величина будет безразмерной (размерность сократится) и носит название коэффициент.
Часто применяется искусственная размерность коэффициентов. Она получается путем их умножения:
Искусственная размерность коэффициентов применяется, как правило, в разговорной речи и при формулировании результатов, а в самих расчетах она не используется. Чаще всего применяются проценты, в которых принято выражать полученные значения относительных величин.
Чаще вместо названия относительная статистическая величина используется более краткий термин-синоним — индекс (от лат. index — показатель, коэффициент).
В зависимости от видов соотносимых абсолютных величин при расчете относительных величин, получаются разные виды индексов: динамики, планового задания, выполнения плана, структуры, координации, сравнения, интенсивности.
Индекс динамики
Индекс динамики (коэффициент роста, темп роста) показывает во сколько раз изменилось изучаемое явление или процесс во времени. Рассчитывается как отношение значения абсолютной величины в отчетный (анализируемый) период или момент времени к базисному (предыдущему):
.
Здесь и далее подиндексы означают: 1 — отчетный (анализируемый) период, 0 — базисный (прошлый) период.
Индекс планового задания
Индекс планового задания – это отношение планового значения абсолютной величины к базисному:
Например, автосалон в январе продал 100 автомобилей, а на февраль запланировал продать 120 автомобилей. Тогда индекс планового задания составит i пз = 120/100 = 1,2, что означает планирование роста продаж в 1,2 раза или на 20%
Индекс выполнения плана
Индекс выполнения плана – это отношение фактически полученного значения абсолютной величины в отчетном периоде к запланированному:
Например, автосалон в феврале продал 110 автомобилей, хотя на февраль было запланировано продать 120 автомобилей. Тогда индекс выполнения плана составит i вп = 110/120 = 0,917, что означает выполнение плана на 91,7%, то есть план недовыполнен на (100%-91,7%) = 8,3%.
Перемножая индексы планового задания и выполнения плана, получим индекс динамики:
В рассмотренном ранее примере про автосалон, если перемножим полученные значения индексов планового задания и выполнения плана, то получим значение индекса динамики: 1,2*0,917 = 1,1.
Индекс структуры
Индекс структуры показывает, какую долю составляет отдельная часть совокупности от всей совокупности.
Например, если в рассматриваемой группе студентов 20 девушек и 10 молодых людей, тогда индекс стурктуры (доля) девушек будет равен 20/(20+10) = 0,667, то есть доля девушек в группе составляет 66,7%.
Индекс координации
Индекс координации показывает, во сколько раз больше или сколько процентов составляет одна часть статистической совокупности по сравнению с другой ее частью, принятой за базу сравнения.
Например, если в группе студентов из 20 девушек и 10 молодых людей, принять за базу сравнения численность девушек, тогда индекс координации численности молодых людей составит 10/20 = 0,5, то есть численность молодых людей составляет 50% от численности девушек в группе.
Индекс сравнения
где А, Б — признаки сравниваемых объектов или территорий.
Индекс интенсивности
Например, хлебный магазин продал 500 буханок хлеба и заработал на этом 10000 руб., тогда индекс интенсивности составит 10000/500 = 20 [руб./бух.хлеба], то есть цена продажи хлеба составила 20 руб. за буханку.
Большинство величин с дробной размерностью представляют собой индексы интенсивности.
Абсолютное значение
Если вместо 3) выполняется более сильное условие:
3a)|x+y| ≤ max(|x|,|y|), то нормирование называется неархимедовым.
Значение | x | (иногда обозначаемое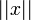 
) называется нормой элемента x. Если упорядоченное поле P является полем действительных чисел R, то нормирование часто называют абсолютным значением.
Содержание
Примеры нормирований
Свойства нормы
Пусть данное условие выполнено. Тогда для любых элементов x и y из поля F имеем:
Извлекая из обеих частей корень и переходя к пределу при n→∞ получаем условие 3a). Обратное утверждение очевидно.
Нормированное поле как метрическое пространство
Из свойств 1-3 немедленно следует, что определяя расстояние между двумя элементами действительнозначного нормированного поля F как норму разности |x-y| мы превращеем его в метрическое пространство, в случае неархимедовой нормы — в ультраметрическое пространство. Разные нормы определяют разные метрики. Если при этом они определяют одинаковую топологию в F, то такие нормы называются зависимыми.
Пополнение
Как и для любого метрического пространства можно ввести понятие полноты и доказать, что любое нормированное поле F изоморфно вкладывается в полное нормированное поле F*, то есть существует изоморфизм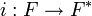 
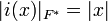
. Норма в F* продолжает норму в F, то есть для каждого x из F: 
, причём F плотно в F* относительно этой нормы. Любое такое поле F* определено однозначно с точностью до изоморфизма, сохраняющего нормы (изометрии) и тождественного на F; оно называется пополнением поля F.
Пример. Пополнением поля рациональных чисел Q с p-адической метрикой является поле p-адических чисел Qp.
Литература
См. также
Полезное
Смотреть что такое «Абсолютное значение» в других словарях:
абсолютное значение — [Интент] Параллельные тексты EN RU The measured voltage value is displayed both as a per unit quantity referred to the nominal voltage of the P63x and as a primary quantity. [Schneider Electric] Измеренное значение напряжения отображается как в… … Справочник технического переводчика
абсолютное значение — absoliučioji vertė statusas T sritis fizika atitikmenys: angl. absolute value vok. Absolutwert, m rus. абсолютное значение, n pranc. valeur absolue, f … Fizikos terminų žodynas
АБСОЛЮТНОЕ ЗНАЧЕНИЕ — См. значение абсолютное … Толковый словарь по психологии
абсолютное значение числа — модуль числа абсолютная величина числа — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] абсолютное значение Величина числа без учета его знака. Так, числа +18 и 18 имеют одно и то же абсолютное… … Справочник технического переводчика
абсолютное значение погрешности — Значение погрешности без учета ее знака (модуль погрешности). Примечание. Необходимо различать термины абсолютная погрешность и абсолютное значение погрешности. [РМГ 29 99] Тематики метрология, основные понятия EN absolute value of an error FR… … Справочник технического переводчика
Абсолютное значение мощности побочных излучений — Значение уровня побочных излучений, выраженное в единицах мощности (мВт, мкВт), подаваемой в фидер антенны на частоте побочного излучения Источник … Словарь-справочник терминов нормативно-технической документации
Абсолютное значение мощности побочных колебаний — Значение уровня побочных колебаний, выраженное в единицах мощности (мВт, мкВт) Источник … Словарь-справочник терминов нормативно-технической документации
абсолютное значение ошибки — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва] Тематики электротехника, основные понятия EN absolute error … Справочник технического переводчика
Нельзя так просто взять и вычислить абсолютное значение
Кажется, задача вычисления абсолютного значения (или модуля) числа совершенно тривиальна. Если число отрицательно, давайте сменим знак. Иначе оставим как есть. На Java это будет выглядеть примерно так:
Вроде бы это слишком просто даже для вопроса на собеседовании на позицию джуна. Есть ли тут подводные камни?
Этот метод JIT-компилятор в идеале может вообще удалить полностью, потому что речь идёт просто про реинтерпретацию набора бит в процессоре, чтобы типы данных сошлись. А сами биты остаются одни и те же и процессору обычно наплевать на типы данных. Хотя говорят, что всё-таки это может привести к пересылке из регистра с плавающей точкой в регистр общего назначения. Но всё равно очень быстро.
Ладно, у нас осталось два ветвления для всех положительных чисел и нулей. Всё равно кажется, что много. Мы знаем, что ветвления — это плохо, если branch predictor не угадает, они могут очень дорого стоить. Можно ли сделать меньше? Оказывается, можно любой нуль превратить в положительный, если вычесть его из 0.0 :
Таким образом, можно написать:
Отлично, у нас теперь всегда одна ветка. Победа? Но как насчёт сделать всегда ноль веток? Возможно ли это?
Этот способ действительно не содержит ветвлений, и профилирование показывает, что пропускная способность метода при определённых условиях увеличивается процентов на 10%. Предыдущая реализация с одним ветвлением была в стандартной библиотеке Java с незапамятных времён, а вот в грядущей Java 18 уже закоммитили улучшенную версию.
В ряде случаев, впрочем, эти улучшения ничего не значат, потому что JIT-компилятор может использовать соответствующую ассемблерную инструкцию при её наличии и полностью проигнорировать Java-код. Например, на платформе ARM используется инструкция VABS. Так что пользы тут мало. Но всё равно интересная статья получилась!
Абсолютная величина. Модуль.
Абсолютными величинами называются — объем или размер события, которое изучается или явления, процесса, который выражен в соответствующих единицах измерения в конкретных условиях места и времени.Или, другими словами: это просто число без учёта знака (всегда с плюсом).
Абсолютная величина числа или модуль числа x — неотрицательное число, определение которого зависит от типа числа x. Обозначается: |x|.
Если x вещественный, то абсолютная величина – это непрерывная кусочно-линейная функция, которая определяется так, формула:
Обобщением этого понятия есть модуль комплексного числа z=x+iy, иногда называют абсолютной величиной. Его определяют формулой:
Абсолютные величины, виды:
Свойства модуля.
.
Так как частное 
= 
, то 
. В силу предыдущего свойства имеем . Воспользуемся равенством 
, которое справедливо в силу определения модуля числа.
Основные свойства абсолютной величины.
Вещественные числа.
Комплексные числа.
Алгебраические свойства абсолютной величины.
Для каждого 
имеют место следующие соотношения:
Как для вещественных, так и для комплексных a, b имеют место соотношения:
СОДЕРЖАНИЕ
Терминология и обозначения
Определение и свойства
Действительные числа
Поскольку символ квадратного корня представляет собой уникальный положительный квадратный корень (в применении к положительному числу), отсюда следует, что
| Икс | знак равно Икс 2 <\ Displaystyle | х | = <\ sqrt <х ^ <2>>>> 
эквивалентно определению, приведенному выше, и может использоваться как альтернативное определение абсолютного значения действительных чисел.
Ниже приведены некоторые дополнительные полезные свойства. Это либо непосредственные следствия определения, либо подразумеваются четырьмя фундаментальными свойствами, указанными выше.
Два других полезных свойства, касающихся неравенств:
Эти отношения могут использоваться для решения неравенств, связанных с абсолютными величинами. Например:
Абсолютное значение, как «расстояние от нуля», используется для определения абсолютной разницы между произвольными действительными числами, стандартной метрики действительных чисел.
Сложные числа
где х и у являются действительными числами, то абсолютное значение или модуль из г обозначается | z | и определяется
Когда комплексное число z выражается в полярной форме как
Комплексное абсолютное значение разделяет четыре основных свойства, приведенных выше для реального абсолютного значения.
Важно отметить, что свойство субаддитивности (« неравенство треугольника ») распространяется на любой конечный набор из n комплексных чисел как ( z k ) k знак равно 1 п <\ textstyle (z_
Доказательство комплексного неравенства треугольника
Функция абсолютного значения
Связь со знаковой функцией
Функция абсолютного значения действительного числа возвращает его значение независимо от его знака, тогда как функция знака (или знака) возвращает знак числа независимо от его значения. Следующие уравнения показывают взаимосвязь между этими двумя функциями:
Производная
Реальная функция абсолютного значения является примером непрерывной функции, которая достигает глобального минимума там, где производная не существует.
Первообразный
Первообразной (неопределенного интеграла) вещественной функции абсолютного значения
Расстояние
Стандартное евклидово расстояние между двумя точками
Это можно рассматривать как обобщение, поскольку для и реального, то есть в 1-пространстве, согласно альтернативному определению абсолютного значения, а 1 <\ displaystyle a_ <1>> б 1 <\ displaystyle b_ <1>>
Выше показано, что расстояние «абсолютное значение» для действительных и комплексных чисел согласуется со стандартным евклидовым расстоянием, которое они наследуют в результате рассмотрения их как одномерного и двумерного евклидова пространства соответственно.
Свойства абсолютного значения разности двух действительных или комплексных чисел: неотрицательность, тождество неразличимых, симметрия и неравенство треугольника, данные выше, можно рассматривать как мотивирующие более общее понятие функции расстояния следующим образом:
Обобщения
Заказанные кольца
Четыре основных свойства абсолютного значения для действительных чисел могут быть использованы для обобщения понятия абсолютного значения на произвольное поле следующим образом.
Векторные пространства
Опять же, фундаментальные свойства абсолютного значения для действительных чисел могут быть использованы, с небольшими изменениями, для обобщения этого понятия на произвольное векторное пространство.