Что такое абсолютная высотная отметка в геодезии
Абсолютная высота
Абсолютная высота
1) Абсолютная высота, абсолютная отметка или альтиту́да (лат. altitude (в геодезии) — расстояние (в метрах) по вертикали от какой-либо точки на поверхности Земли до среднего уровня поверхности океана, не нарушенного волнением и приливами, или до поверхности геоида.
2) Абсолютная высота — это высота, отсчитываемая от основной уровенной поверхности.
Абсолютная высота представляет собой третью координату точки, дополняющую широту и долготу; на суше определяется при помощи нивелирования. Абсолютная высота точки, лежащей выше уровня океана, считается положительной, ниже — отрицательной.
В России абсолютные высоты точек земной поверхности отсчитывают от среднемноголетнего уровня Балтийского моря, определённого от нуля футштока в Кронштадте. При съёмке местности используют географические координаты и абсолютную высоту ближайших опорных геодезических пунктов.
См. также
Ссылки
Полезное
Смотреть что такое «Абсолютная высота» в других словарях:
Абсолютная высота — [absolutus полный, независимый] расстояние по вертикали от любой точки поверхности Земли до среднего уровня океана. А. в. точек, лежащих выше этого уровня, считается положительной, ниже отрицательной. Геологический словарь: в 2 х томах. М.: Недра … Геологическая энциклопедия
АБСОЛЮТНАЯ ВЫСОТА — высота точки над уровнем моря, определяемая нивелированием, Т. к. уровни морей неодинаковы (напр. Балтийского, Черного и Каспийского), то для возможности сравнения А. в. разных точек в СССР их определяют по отношению к уровню Балтийского моря.… … Технический железнодорожный словарь
Абсолютная высота — высота какой либо точки над уровнем моря. EdwART. Толковый Военно морской Словарь, 2010 … Морской словарь
АБСОЛЮТНАЯ ВЫСОТА — точки земной поверхности (альтитуда) расстояние (обычно в м) по вертикали от этой точки до среднего уровня поверхности океана. В Российской Федерации исчисляется от нуля футштока в Кронштадте … Большой Энциклопедический словарь
абсолютная высота — Расстояние по вертикали от среднего уровня поверхности океана до данной точки земной поверхности. Syn.: альтитуда … Словарь по географии
абсолютная высота — ортометрическая высота точки земной поверхности (альтитуда), расстояние (обычно в метрах) по вертикали от этой точки до среднего уровня поверхности океана.В России исчисляется от нуля футштока в Кронштадте. * * * АБСОЛЮТНАЯ ВЫСОТА АБСОЛЮТНАЯ… … Энциклопедический словарь
абсолютная высота — absoliutusis aukštis statusas T sritis Standartizacija ir metrologija apibrėžtis Aukštis virš jūros lygio. atitikmenys: angl. absolute altitude; true height vok. absolute Höhe, f; wahre Höhe, f rus. абсолютная высота, f pranc. altitude, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
абсолютная высота — absoliutusis aukštis statusas T sritis fizika atitikmenys: angl. absolute altitude; true height vok. absolute Höhe, f; wahre Höhe, f rus. абсолютная высота, f pranc. altitude, f; hauteur au dessus du niveau de la mer, f … Fizikos terminų žodynas
абсолютная высота — absoliutusis aukštis statusas T sritis Kūno kultūra ir sportas apibrėžtis Vertikalus nuotolis (altitudė) nuo kurio nors žemės paviršiaus taško iki vidutinio jūros lygio. Absoliutusis aukštis paprastai reiškiamas metrais. atitikmenys: angl.… … Sporto terminų žodynas
Абсолютная высота — абсолютная отметка (в геодезии), расстояние по вертикали от какой либо точки на поверхности Земли до среднего уровня поверхности океана. Определяется Нивелированием. В СССР А. в. исчисляется от нуля футштока в Кронштадте … Большая советская энциклопедия
Абсолютная и относительная системы высот, их взаимосвязь
В геодезии применяют две системы высот.
1. Абсолютная — расстояние по высоте от среднего уровня Балтийского моря до нашей высоты.
2. Относительная (высотная или условная)— расстояние по высоте от чистого пола 1-го этажа (применяется при типовом проектировании)
Взаимосвязь:
Например строительная площадка в абсолютной системе высот планируется на высоте 132,00м. Средний снежный покров в данной местности достигает 0.8м.Тогда в относительной системе высот высота чистого пола с отметкой 0,0 будет соответствовать высоте 132,8 в абсолютной системе высот.
. 18. Что такое абсолютная высота и превышение, расстояние и горизонтальное понижение?
Абсолютную высоту точки земной поверхности по карте определяют по горизонталям и отметкам. Если точка расположена на горизонтали, то ее высота равна отметке горизонтали. Если точка расположена между горизонталями, то ее высота равна отметке нижней горизонтали плюс превышение точки (определяется интерполированием) над этой горизонталью.
Относительное превышение двух точек равно разности абсолютных высот этих точек.
19. Что такое уклон? В каких единицах он выражается?
Выражается: (на примере уклона, который соответствует подъему 10 м на 1000 м расстояния).
20. Что измеряют теодолитом?
Теодолитом измеряют вертикальные и горизонтальные углы, а также углы наклона.
Угол наклона- это двугранный угол между горизонтальной плоскостью и направлением на предмет. Он может быть положительным и отрицательным.
21. Как уменьшить влияние коллимационной погрешности при створных измерениях?
Коллимационные погрешности влияют на точность измерений горизонтальных и вертикальных углов. Традиционная методика исключения коллимационной погрешности заключается в наблюдении углов при двух положениях круга.
22. Что измеряют нивелиром?
Нивелиром измеряют превышение точек.
23. Как ослабить влияние несоблюдение главного условия нивелира при измерениях превышений?
Чтобы исключить влияние оптико-механических погрешностей при измерении превышений между точками его надо ставить посередине между точками.
24. Как проверить работоспособность нивелира при измерениях превышений?
Поверку можно произвести различными способами. Один из них заключается в том, что на местности на расстоянии примерно 50 м забивают колышки в точках 1 и 2 (рис. 17) и определяют превышение точки 2 – ( 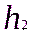

рис. 17.
Первый раз нивелир устанавливают в точке 1, в точке 2 – рейку. Если главное условие не выполняется, т.е. визирная ось не параллельна оси цилиндрического уровня, то вместо правильного отсчёта по рейке 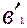
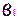
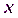
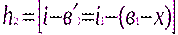
затем нивелир и рейку меняют местами, и тогда
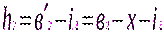
следовательно,
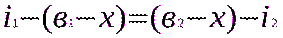
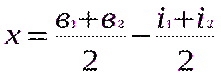
Юстировку можно не проводить, если:
для нивелира Н-3 вычисленное значение х ≤ ± 4 мм;
для нивелира Н-10Л вычисленное значение х ≤ ± 10 мм.
Если погрешность х больше приведенных величин, то необходимо устранить погрешность, действуя исправительными винтами цилиндрического уровня, предварительно установив горизонтальную нить сетки нитей на исправленный отсчет по рейке
У нивелиров с компенсаторами (т.е. у самоустанавливающихся) визирная ось приводится в горизонтальное положение автоматически после предварительного горизонтирования прибора по круглому уровню. Поверка таких нивелиров следующая.
Упрощенный способ поверки главного условия заключается в том, что берутся отсчеты по рейкам при установке нивелира посередине между рейками и в 4–5 м от одной из них. Если разность в полученных значениях превышений не превосходит допустимых величин (± 4 мм или ± 10 мм), то главное условие соблюдено. В необходимом случае исправление производят в мастерской.
25. Что такое визирная ось и ось цилиндрического уровня?
Визирная ось- прямая линия, проходящая через центр глаза, центр сетки нитей и фокус объектива.
Осью цилиндрического уровня называют мнимую линию, касательную к дуге продольного сечения внутренней сферической поверхности ампулы уровня в нульпункте.
Нульпунктом называют среднюю точку шкалы цилиндрического уровня. При наклоне нивелира изображения концов пузырька расходятся. После приведения пузырька круглого уровня в нульпункте – центр концентрических колец – в поле зрения трубы появляется изображение концов половинок пузырька цилиндрического уровня, совмещение которых достигается вращением элевационного винта. Благодаря тому, что шаг элевационного винта мал, выведение им пузырька уровня в нульпункт происходит плавно и точно. Если визирная ось параллельно оси цилиндрического уровня, то после совмещения концов пузырька уровня визирная ось устанавливается в горизонтальное положение. Это выполняется непосредственно перед взятием отсчета по рейке.
Системы высот в геодезии
Понятие высоты, несмотря на кажущуюся очевидность, является одним из наиболее сложных и тонких понятий геодезии. Это связано с двойственным смыслом высоты: с одной стороны, это расстояние между точками в пространстве, т.е. чисто геометрическое понятие; с другой стороны, в физическом понимании, это величина, определяющая энергетический уровень той или иной точки в поле силы тяжести.
Если две точки лежат на одной отвесной линии, геометрическую высоту можно измерить непосредственно как расстояние между ними; так измеряют высоты различных предметов (высота геодезического сигнала, инструмента над центром, высота человека, дерева, дома и т.д.). Очевидно, что геодезическую высоту, т.е. высоту в геометрическом смысле, так измерить нельзя: в точке поверхности Земли неизвестны ни направление нормали к эллипсоиду, вдоль которой нужно измерять высоту, ни положение отсчетной точки на эллипсоиде, которая к тому же физически недоступна, поскольку эллипсоид проходит, как правило, внутри Земли.
Физическое понятие высоты связано с работой в поле силы тяжести. Так, если точки лежат на одной уровенной поверхности, например, на поверхности какого-либо водоема, где отсутствуют течения, естественно, считать, что высоты этих точек одинаковы. Если же вода течет от одной точки к другой, говорят, что высота первой точки больше. В этом случае мерой высоты выступает работа, которую совершает сила тяжести при перемещении водной часы, т.е. разность потенциалов между указанными точками. Поскольку потенциал на уровенной поверхности постоянен, разность потенциалов любых точек, лежащих на двух различных уровенных поверхностях, всегда постоянна. Поэтому разность потенциалов является мерой высоты или высотой в физическом понимании. Как известно, разность потенциалов можно получить в результате геометрического нивелирования и измерений силы тяжести.
Еще одной причиной, по которой высоту рассматривают и изучают отдельно от плановых координат, является различие в методах получения этих величин: до недавнего времени плановые координаты находили из обработки линейных и угловых измерений, выполненных на поверхности Земли, а высоты преимущественно из геометрического нивелирования, сопровождаемого измерениями силы тяжести. Определение высоты по измерениям расстояний и вертикальных углов затруднено из-за влияния вертикальной рефракции, из-за чего вертикальные углы измеряют со значительно меньшей точностью, чем горизонтальные.
Спутниковые методы позволяют определить прямоугольна координаты точек поверхности Земли, по которым, используя зависимости математических формул, можно найти геодезические координаты. Однако так можно найти только высоту в геометрическом понимании, поскольку прямоугольные координаты не содержат информации о поле силы тяжести. Кроме того, из-за тропосферных влияний и методических особенностей высота и в этом случае определяется с несколько меньшей точностью, чем плановые координаты.
Что такое высота и где ее начало
Для определения положения точки, находящейся на физической поверхности Земли относительно исходной уровенной поверхности, помимо плоских координат, необходима третья координата — высота Н.
Высота – это измерение объекта или его местоположения, отмеряемое в вертикальном направлении. Высота в любой точки земной поверхности отсчитывается от разных поверхностей, таких как геоид, квазигеоид или референц-эллипсоид.
Геоид, квазигеоид и эллипсоид вращения
Геоид — это образованная основной уровенной поверхностью замкнутая фигура принимаемая за обобщенную поверхность Земли. Поверхность геоида является одной из уровенных поверхностей потенциала силы тяжести. Эта поверхность, мысленно продолженная под материками, образует замкнутую фигуру, которую принимают за сглаженную фигуру Земли. Часто под геоидом понимают уровенную поверхность, проходящую через некоторую фиксированную точку земной поверхности у берега моря. Понятие о геоиде сложилось в результате длительного развития представлений о фигуре Земли как планеты, а самый термин «геоид» предложен И. Листингом в 1873 г. От геоида отсчитывают абсолютные высоты. По современным данным, средняя величина отступления геоида от наиболее удачно подобранного эллипсоида составляет около ±50 м, а максимальное отступление не превышает ±100 м. Высота геоида в сумме с ортометрической высотой определяет высоту Н соответственной точки над земным эллипсоидом. Поскольку распределение плотности внутри Земли с необходимой точностью неизвестно, высоту Н в геодезической гравиметрии и геодезии, согласно предложению М. С. Молоденского, определяют как сумму нормальной высоты и высоты квазигеоида. Для точного определения поверхности геоида какой-либо точки необходимо выполнить комплекс измерений, непосредственно на поверхности геоида. Что практически не возможно, либо в соответствующей точке на физической поверхности Земли с учетом распределения масс в этом месте, что также не предоставляется возможным. По этой причине было предложено вместо поверхности геоида использовать квазигеоид.
Квазигеоид — это поверхность близкая к поверхности геоида, определяемая только по результатам измерений на земной поверхности без привлечения данных по распределению масс. Поверхность квазигеоида определена значениями потенциала силы тяжести на земной поверхности, и для изучения квазигеоида результаты измерений не нужно редуцировать внутрь притягивающей массы. Квазигеоид отступает от геоида в высоких горах на 2–4 м, на низменных равнинах — на 0,02-0,12 м, на морях и океанах поверхности геоида и квазигеоида совпадают.
Фигуру квазигеоида определяют методом астрономо-гравиметрического нивелирования или через предварительное определение возмущающего потенциала по материалам наземных гравиметрических съёмок и наблюдений за движением искусственных спутников Земли. Последние данные необходимы в связи с недостаточной гравиметрической изученностью некоторых областей Земли Поверхность геоида, из-за ее сложности, математически никак не выражается, поэтому на ней нельзя решать геодезические задачи. Для решения таких задач взамен поверхности геоида принимают поверхность эллипсоида вращения.
Эллипсоида вращения — это близкая по форме к геоиду поверхность, но математически правильная, на которую можно перенести результаты измерений, выполненных на физической поверхности Земли. Эллипсоид вращения, размеры которого подбираются при условии наилучшего соответствия фигуре квазигеоида для Земли в целом (общеземной эллипсоид) или отдельных её частей (референц-эллипсоид). Для России принят референц-эллипсоид Крассовского форма и размеры которого были вычислены советским геодезистом А. А. Изотовым, и который в 1940 году назван именем Ф. Н. Красовского.
Высота точки местности в географии, топографии и геодезии может измеряться от разных уровней отсчёта:
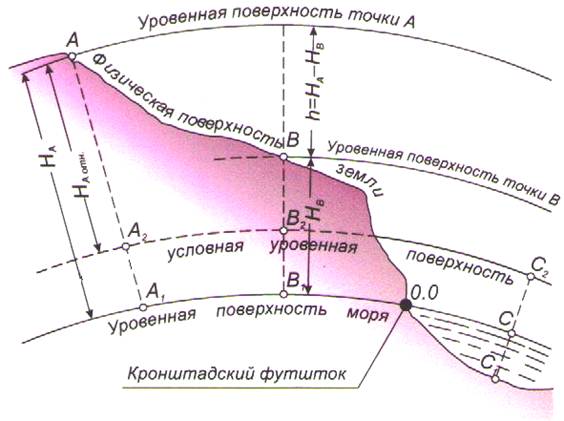
1. Абсолютная высота отсчитывается от уровня моря или геоида (линия НА и линия НВ);
2. Относительная высота (превышение) отсчитывается от какого-либо условного уровня (линия НС);
3. Геодезическая (эллипсоидальная) высота — высота относительно эллипсоида вращения.
Абсолютная и относительная высоты
В нашей стране с 1946 г. счет абсолютных высот ведется от нуля Кронштадтского футштока соответствующего среднему уровню Балтийского моря в спокойном его состоянии (Балтийская система высот). Вся нивелирная сеть на территорию России опирается на один исходный пункт, не имеет внешнего контроля и уравнивается как свободная система. В середине 1980-х в связи с предстоящим строительством гидротехнического комплекса защиты Ленинграда (ныне Санкт-Петербурга) от наводнений были созданы дублеры в Кронштадте и г. Ломоносове (на основе репера № 6521 и маяка Шепелевский)
Высоты, отсчитанные от иной уровенной поверхности, называются относительными на рисунке изображены линией НС. При съемке небольших участков, при обмерных работах, а также на стройплощадке часто применяют относительную или условную систему отсчета высот.
Что такое превышение
Численное значение высоты точки называется отметкой точки. Разность высот двух точек, называется превышением. Превышение h точки В над точкой А, равное разности высот точек А и В, определяется как h = НВ – НА. Зная высоту точки А, для определения высоты точки В на местности измеряют превышение hAB. Высоту точки В вычисляют по формуле HВ = HA + hAB. Измерение превышений и последующее вычисление высот точек называется нивелированием.
Геодезическая высота
Геодезической (эллипсоида́льной) высотой некоторой точки физической поверхности земли называется отрезок нормали к эллипсоиду от его поверхности до данной точки. Вместе с геодезическими широтой и долготой (B и L соответственно) она определяет положение точки относительно заданного эллипсоида. Физически эллипсоида не существует, следовательно геодезическая высота не может быть непосредственно измерена наземными методами. Определить её возможно с помощью спутниковых измерений, а также посредством обработки рядов триангуляции, астрономо-геодезического нивелирования.
Как видно из определения геодезическая высота зависит от расположения и параметров выбранного эллипсоида, поэтому геодезическую высоту разделяют на две части. Одна из них характеризует физическую поверхность Земли относительно уровенной поверхности (информацию о ней получают в большей степени нивелированием), вторая, более гладкая, характеризует отличие отсчётного эллипсоида от геоида. Первую часть называют гипсометрической, а вторую — гладкой или геоидальной частью. Уровенная поверхность имеет несравненно более плавную форму в сравнении с физической, следовательно геоидальная часть меняется гораздо медленнее гипсометрической.
Системы геодезических высот
Ортометрическая высота точки — это расстояние (H) вдоль отвесной линии от точки до поверхности геоида. Ортометрическая высота для практических целей является «высотой над уровнем моря». Чтобы вычислить значение ортометрической высоты, нужно знать плотность пород вдоль силовой линии или измерять силу тяжести внутри Земли. Поэтому ортометрическую высоту нельзя найти по измерениям только на поверхности Земли. Альтернативой ортометрической высоте являются нормальная высота. Ортометрические высоты по Гельмерту используют многие европейские страны, Турция и страны Американского континента. Поскольку гравитация не является постоянной на больших площадях, ортометрическая высота также не является постоянной. Так на территории США гравитация на 0,1% сильнее на севере Соединенных Штатов, чем на юге, поэтому ровная поверхность, имеющая ортометрическую высоту в 1000 метров в Монтане, будет иметь высоту в 1001 метр в Техасе.
Нормальные высоты — это высоты от поверхности квазигеоида, один из нескольких типов высоты. Нормальная высота точки вычисляется из геопотенциальных чисел путем деления геопотенциального числа точки, т. е. ее разности геопотенциалов с уровнем моря, на среднюю нормальную гравитацию, вычисленную вдоль отвеса точки. (Точнее, вдоль эллипсоидной нормали, усредняя по диапазону высот от 0-эллипсоид-H*; процедура, таким образом, рекурсивна. Нормальные высоты, таким образом, зависят от выбранного опорного эллипсоида. Система нормальных высот принята в России, странах СНГ и некоторых европейских странах (Швеция, Германия, Франция и др.). Нормальные значения гравитации можно вычислить через плотность земной коры вокруг отвеса. Нормальные высоты занимают видное место в теории гравитационного поля Земли, разработанной школой М. С. Молоденского. Эталонная поверхность, с которой измеряются нормальные высоты, называется квазигеоидом, представляющим собой «средний уровень моря», аналогичный геоиду и близкий к нему, но лишенный физической интерпретации эквипотенциальной поверхности. В геодезии (топографии) нормальную высоту называют абсолютной, а разность нормальных высот — относительной высотой. Численное значение абсолютной высоты принято называть отметкой.
Геопотенциальное число ― это та работа, которую нужно совершить, чтобы подняться от уровня моря до точки Р поверхности Земли.
Динамическая высота — это геопотенциальное число, переведенное в линейную меру, получить его можно разделив геопотенциальное число на любое постоянное значение С силы тяжести. Выбирая в качестве С разные значения постоянной, можно построить разные системы динамических высот. Динамические вы соты были введены К.Ф.Гауссом, который предложил рассматривать высоты как геопотенциальные числа, т.е. принять С = 1. Динамическая высота постоянна, если следовать одному и тому же гравитационному потенциалу, когда они перемещаются с места на место. Из-за изменения силы тяжести поверхности, имеющие постоянную разницу в динамической высоте, могут быть ближе или дальше друг от друга в различных местах. Динамические высоты обычно выбираются так, чтобы они имели сопряжения с геоидом. Когда оптическое выравнивание выполнено, путь близко соответствует следующему значению динамической высоты по горизонтали, но не ортометрической высоте для вертикальных изменений, измеренных на выравнивающем стержне. Таким образом, небольшие поправки должны быть применены к полевым измерениям, чтобы получить либо динамическую высоту, либо ортометрическую высоту, обычно используемую в технике. Паспорта данных Национальной Геодезической службы США дают как динамические, так и ортометрические значения. Динамическая высота может быть вычислена с использованием нормальной силы тяжести на 45-градусной широте и геопотенциального числа местоположений.
Абсолютные, условные отметки и превышения



Для полной характеристики положения точки на поверхности Земли необходимо знать еще третью координату – высоту.
Высотой точки называется расстояние по отвесному направлению от этой точки до уровенной поверхности. Числовое значение высоты точки называется ее отметкой.
Принято считать, что высота уровенной поверхности Земли равна нулю. Точки, лежащие выше этой уровенной поверхности, имеют положительную высоту, а ниже отрицательную.
В РФ за начало счета высот принят средний уровень воды в Финском заливе Балтийского моря, установленный из многолетних наблюдений. Этот средний уровень отмечен награвированной чертой на металлической пластине, вмурованной в гранитный устой одного из мостов в Кронштадте, и называется нулем Кронштадтского футштока. От этого нуля и ведется счет высот на всей территории страны.
Высоты точек, определяемые относительно уровенной поверхности, проходящей через эту черту, составляют Балтийскую систему высот.
Рис. 6. Уровенная поверхность, абсолютные, условные отметки и превышения
Различают отметки:
1. Абсолютной отметкой (рис. 6) называют высоту точки над уровенной поверхностью моря (отрезки АА1 и ВВ1 абсолютные отметки точек А и В).
2. Условной отметкой (рис. 6) называют высоту точки над какой – либо условной уровенной поверхностью (отрезки АА2 и ВВ2 условные отметки этих точек).
Точка С1 лежит ниже уровенной поверхности моря, ее абсолютная отметка – отрезок С1С – имеет знак минус.
На рисунке 7 точка 2 находится выше точки 1. Чтобы определить, насколько одна точка расположена выше или ниже другой, находят превышение между ними, т.е. разность отметок двух точек. Превышение может быть положительным или отрицательным в зависимости от того, как оно определяется относительно данных точек.