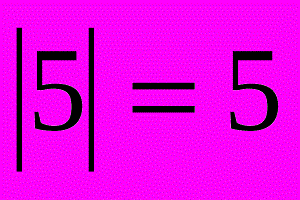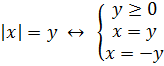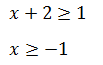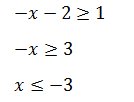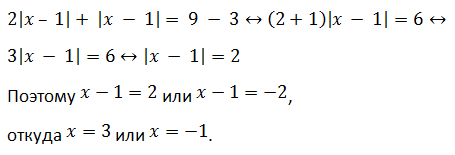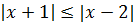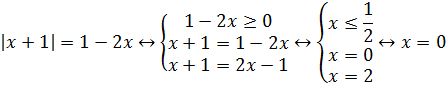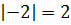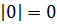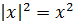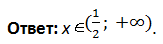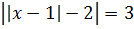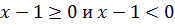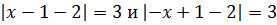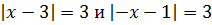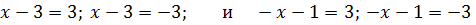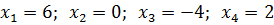Что такое абсолютная величина разности

20.04.202227.04.2022 admin 0 Comments

Абсолютная величина. Модуль.

Абсолютными величинами называются — объем или размер события, которое изучается или явления, процесса, который выражен в соответствующих единицах измерения в конкретных условиях места и времени.Или, другими словами: это просто число без учёта знака (всегда с плюсом).

Абсолютная величина числа или модуль числа x — неотрицательное число, определение которого зависит от типа числа x. Обозначается: |x|.

Если x вещественный, то абсолютная величина – это непрерывная кусочно-линейная функция, которая определяется так, формула:

Обобщением этого понятия есть модуль комплексного числа z=x+iy, иногда называют абсолютной величиной. Его определяют формулой:

Абсолютные величины, виды:

Свойства модуля.

Так как частное = , то . В силу предыдущего свойства имеем . Воспользуемся равенством , которое справедливо в силу определения модуля числа.

Основные свойства абсолютной величины.

Вещественные числа.

Комплексные числа.

Алгебраические свойства абсолютной величины.

Для каждого имеют место следующие соотношения:

Как для вещественных, так и для комплексных a, b имеют место соотношения:

Источник

Нельзя так просто взять и вычислить абсолютное значение

Кажется, задача вычисления абсолютного значения (или модуля) числа совершенно тривиальна. Если число отрицательно, давайте сменим знак. Иначе оставим как есть. На Java это будет выглядеть примерно так:

Вроде бы это слишком просто даже для вопроса на собеседовании на позицию джуна. Есть ли тут подводные камни?

Этот метод JIT-компилятор в идеале может вообще удалить полностью, потому что речь идёт просто про реинтерпретацию набора бит в процессоре, чтобы типы данных сошлись. А сами биты остаются одни и те же и процессору обычно наплевать на типы данных. Хотя говорят, что всё-таки это может привести к пересылке из регистра с плавающей точкой в регистр общего назначения. Но всё равно очень быстро.

Ладно, у нас осталось два ветвления для всех положительных чисел и нулей. Всё равно кажется, что много. Мы знаем, что ветвления — это плохо, если branch predictor не угадает, они могут очень дорого стоить. Можно ли сделать меньше? Оказывается, можно любой нуль превратить в положительный, если вычесть его из 0.0 :

Таким образом, можно написать:

Отлично, у нас теперь всегда одна ветка. Победа? Но как насчёт сделать всегда ноль веток? Возможно ли это?

Этот способ действительно не содержит ветвлений, и профилирование показывает, что пропускная способность метода при определённых условиях увеличивается процентов на 10%. Предыдущая реализация с одним ветвлением была в стандартной библиотеке Java с незапамятных времён, а вот в грядущей Java 18 уже закоммитили улучшенную версию.

В ряде случаев, впрочем, эти улучшения ничего не значат, потому что JIT-компилятор может использовать соответствующую ассемблерную инструкцию при её наличии и полностью проигнорировать Java-код. Например, на платформе ARM используется инструкция VABS. Так что пользы тут мало. Но всё равно интересная статья получилась!

Источник

Модуль числа знак, свойства, действия, как найти, примеры графиков

Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.

Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам.

Что такое модуль в математике

Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.

Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.

Свойства модуля

Важно помнить о следующих свойствах:

Модуль комплексного числа

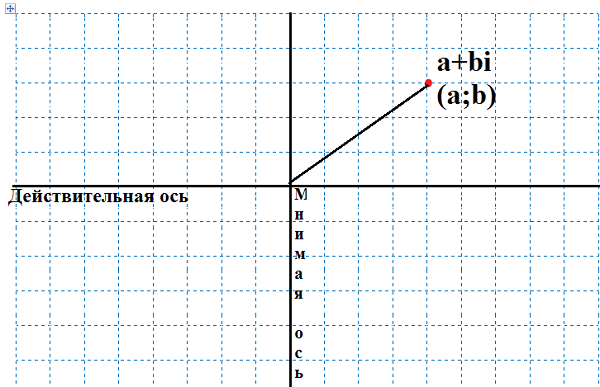
Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).

Этот направленный отрезок также является вектором, представляющим комплексное число a + bi, поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi.

Как решать уравнения с модулем

Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.

Уравнения типа |x| = a

Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.

Равенство с абсолютной величиной не имеет решения, если величина отрицательная.

Если |x| &lt, a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.

Уравнения типа |x| = |y|

Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.

Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).

Далее простая арифметика − нужно решить два равенства относительно x.

Уравнения типа |x| = y

Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.

Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:

Решение неравенств с модулем

Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.

Уравнения вида |x| = a

Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.

Решение.

Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.

После перемещения константы вправо получено: |x| = 2.

Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.

Ответ: 2 и −2.

Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.

Решение.

Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.

Это означает, что –2 – поворотная точка.

Далее определяется знак на интервалах: на промежутке величина будет отрицательной, а на интервале будет положительной.

Разделим интервал на 2 части:

Общим ответом для этих двух неравенств является интервал [−1, + ∞).

Общим ответом для этих двух неравенств является интервал (−∞, –3].

Окончательное решение – объединение ответов отдельных частей:

Ответ: x ∈ (–∞, –3] ∪ [–1, + ∞).

Уравнения вида |x| = |y|

Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.

Решение:

Ответ: x1 = 3, x2 = − 1.

Пример 2 (алгебра 8 класс). Решить неравенство:

Решение:

Уравнения вида |x| = y

Пример 1 (алгебра 10 класс). Найти x:

Решение:

Ответ: x = 0.

Модуль суммы

Модуль разности

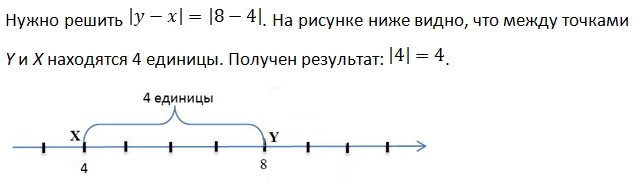
Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.

Пример 1.

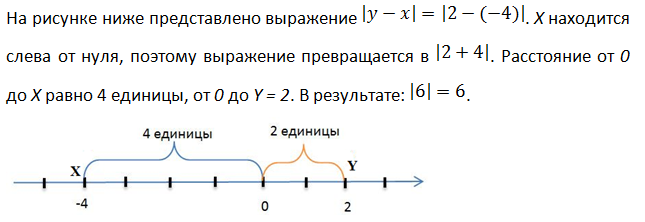
Пример 2.

Модуль отрицательного числа

Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,

Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.

Модуль нуля

Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.

Модуль в квадрате

Модуль в квадрате всегда равен выражению в квадрате:

Примеры графиков с модулем

Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.

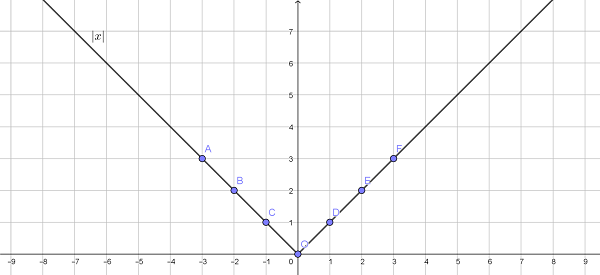
Пример 1.

Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.

Решение:

Объяснение: из рисунка видно, что график симметричен относительно оси Y.

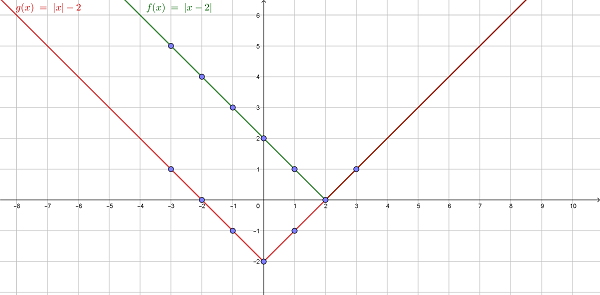
Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.

Решение:

Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).

Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.

Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.

Метод интервалов в задачах с модулем

Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.

Для использования метода нужно совершить следующие действия:

Пример 1. Решить методом интервалов.

Решение:

Результатом будет сумма всех подходящих интервалов.

Модуль в модуле

Среди примеров часто встречаются уравнения, где нужно найти корни равенств такого вида: ||ax – b| – c| = kx + m.

Лучше всего понять принцип на примере.

Пример 1. Решить

Решение:

Первым делом нужно раскрыть внутренний модуль. Для этого рассматривается два варианта:

В первом случае выражение положительное, а во втором отрицательное. Исходя из этого, получаем:

Нужно упростить два уравнения:

Далее каждое из равенств разделяется еще на два:

Получено четыре результата:

Заключение

Самое важное, что нужно знать: модуль не может быть отрицательным.

Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов.

В качестве итогов, напомним все свойства, которые помогут в решении задач:

Решать равенства и неравенства можно разными способами, но лучше всего использовать графический способ или метод интервалов.

Источник

Элективный курс по математике «Абсолютная величина»

Разделы: Математика

Основное содержание курса

Абсолютная величина числа. Основные свойства (1ч).

Определение абсолютной величины числа или модуля. Аналитическая запись определения. Геометрический смысл. Основные свойства. Историческая справка.

Основная цель – систематизировать и обобщить знания обучающихся по теме “Абсолютная величина”, полученные ими в 6 и 8 классах; рассмотреть геометрический смысл абсолютной величины и основные свойства; дать историческую справку о введении термина “модуль” и “знак модуля”; рассмотреть примеры, решение которых основано на определении модуля.

Решение уравнений с модулями (3ч).

Решение линейных, квадратных уравнений с модулями, а также уравнений, содержащих абсолютную величину, с параметрами.

Основная цель – геометрическая интерпретация выражения и использование ее для решения уравнений вида ; рассмотреть решение линейных уравнений, основанных на определении модуля; решение квадратных уравнений, содержащих знак абсолютной величины, а также графическое решение уравнений, содержащих абсолютную величину, с параметрами.

Решение неравенств с модулями (3ч).

Решение линейных, квадратных неравенств с модулями, а также неравенств, содержащих абсолютную величину, с параметрами.

Основная цель – выработать умения решать линейные неравенства с модулем различными способами (используя геометрический смысл, возведение неравенства в квадрат, с помощью двойного неравенства); квадратные неравенства, содержащие знак абсолютной величины, используя схематический набросок графика квадратной функции, а также метод интервалов; дать представление о решении неравенств, содержащих абсолютную величину, с параметрами.

Метод интервалов (2ч).

Решение уравнений и неравенств, содержащих абсолютную величину, методом интервалов.

Основная цель – научить школьников решать уравнения и неравенства, содержащие абсолютную величину, методом интервалов; сформулировать теорему, на которой основано отыскание интервалов знакопостоянства; нахождение нулей модуля.

Неравенства вида , , решаемые посредством равносильных переходов (2ч).

Решение неравенства вида посредством равносильных переходов к совокупности неравенств , а неравенства — к системе неравенств .

Основная цель – закрепить понятие равносильности, известное учащимся из 8 класса; сформулировать (а в “сильном” классе доказать) свойство равносильного перехода от неравенства к совокупности и от неравенства к системе .

Применение свойств абсолютной величины при решении уравнений и неравенств (1ч).

Решение уравнений и неравенств (линейных, квадратных, степени выше второй), а также систем уравнений и неравенств с помощью свойств абсолютной величины.

Основная цель – повторить при необходимости основные свойства модуля; научить обучающихся решать уравнения и неравенства (линейные, квадратные, степени выше второй), а также систем уравнений и неравенств с помощью свойств абсолютной величины; показать графические приемы при записи ответа; расширить класс уравнений с модулем (рассмотреть уравнение с двумя переменными).

Решение уравнений и неравенств с модулем на координатной прямой (1ч).

Решение линейных уравнений и неравенств с модулем на координатной прямой.

Основная цель – повторить формулу расстояния между двумя точками А(х₁) и В(х₂) координатной прямой; научить обучающихся решению уравнений и неравенств с модулем на координатной прямой.

Модуль и преобразование корней (1ч).

Применение понятия модуля при оперировании арифметическими корнями. Преобразование иррациональных выражений, при решении которых используется модуль.

Основная цель – выработать умение выполнять преобразования выражений, содержащих квадратный корень, при которых используется модуль.

Модуль и иррациональные уравнения (2ч).

Решение иррациональных уравнений с использованием метода выделения полного квадрата или введения новой переменной.

Основная цель – повторить известное обучающимся из 8 класса определение иррациональных уравнений; показать на примерах решение иррациональных уравнений, связанных с необходимостью использования модуля.

Учебно-тематический план

№ п/п	Тема	Количество часов	Форма проведения занятий	Форма контроля	Наименование образовательного продукта
1	Абсолютная величина числа. Основные свойства.	1	лекция	—	—
2 4	Решение уравнений с модулями: изучение нового материала	решение контрольных заданий решение контрольных заданий проверка рабочих тетрадей	—
5 7	Решение неравенств с модулями: изучение нового материала	проверка домашнего задания проверка рабочих тетрадей	—
8 9	Метод интервалов.	1 1	комбинированный урок урок-соревнование	ответы на вопросы урок взаимопроверки	—
10 11	Решение неравенств вида , , решаемые посредством равносильных переходов.	1 1	изучение нового материала закрепление изученного материала	проверка конспектов математический диктант	—
12	Применение свойств абсолютной величины при решении уравнений и неравенств.	1	обобщение и систематизация знаний	устный опрос	—
13	Решение уравнений и неравенств с модулем на координатной прямой.	1	обобщение и систематизация знаний	самостоятельная работа	—
14	Модуль и преобразование корней.	1	практикум	работа в группах	—
15 16	Модуль и иррациональные уравнения.	1 1	проверка и коррекция ЗУН консультация	домашняя контрольная работа ответы на вопросы	—
17	Зачет.	1	контрольная или тестовая работа	—	составление опорного конспекта

Методические материалы

Занятие №1: Определение абсолютной величины числа (модуля числа), его геометрический смысл и основные свойства.

Абсолютной величиной (или модулем) действительного числа а называется само это число, если оно неотрицательное, и это число, взятое с противоположным знаком, если оно отрицательное.

Модуль числа а обозначается так:. Устанавливая связь между модулем числа и самим числом, получим аналитическую запись определения:

Модулем числа называется также расстояние от начала отсчета до точки, изображающей это число на координатной прямой. В этом состоит геометрический смысл модуля. Т.о. используются термины “модуль”, “абсолютная величина” или “абсолютное значение” числа. В соответствии с приведенным определением = 5, = 3, =0. Модуль числа может быть определен и как наибольшее из чисел а и – а.

Историческая справка: термин “модуль” (от лат.modulus – мера) ввел английский математик Р. Котес (1682—1716), а знак модуля немецкий математик К.Вейерштрасс (1815-1897), в 1841 г.

Рассмотрим примеры, решение которых основано на определении модуля.

№ 1. Решить уравнение =4.

По определению модуля; х=4 или х =-4.

№ 2. Решить уравнение: =3.

Уравнение равносильно совокупности двух уравнений:

№ 3. Решить уравнение: =-2.

По свойству 1: модуль любого действительного числа есть число неотрицательное, делаем вывод, что решения нет.

№ 4. Решить уравнение: =х–5.

По этому же свойству 1: х–50, х5.

№ 5. Решить уравнение: +х=0.

=- х, х0.

№ 6. Решить уравнение: =х+2.

В отличие от предыдущего примера в правой части данного уравнения содержится выражение с переменной. Поэтому уравнение имеет решение при условии, что х +20,т.е. х-2. Тогда имеем:

Т.о. при х -2, имеем:

Упражнения для самостоятельной работы:

Занятие №2. Решение линейных уравнений с модулями.

При решении линейных уравнений используется или геометрический смысл модуля числа или раскрытие знака модуля. Рассмотрим на примере: решить уравнение

+ = 7.

В интервале 1 (х 5) получаем: (х-5)+(х+2)=7 или 2х-3=7, откуда х=5. Точка х=5 в рассматриваемый промежуток не входит и не является решением уравнения.

Итак, решение данного уравнения: -2х5.

Упражнения для самостоятельной работы:

№1. х=+,

№2. ++=2,

№3. +—=2х+4,

№4. ++=11,

№5. -2=0.

Занятие №3. Решение квадратных уравнений с модулем.

Рассмотрим решение квадратных уравнений с модулями на примерах:

№1. Решить уравнение

Введем замену =у, тогда при у 0 уравнение принимает вид:

№2. Решить уравнение:

+ = 0.

Уравнение равносильно системе: Откуда х=1.

№3. Решить уравнение:

= 2х – 1.

Уравнение имеет решение при условии, что 2х–10, а равенство возможно при условии: значения выражений х 2 +х–1 и 2х–1 одинаковы либо противоположны. Т.о. имеем: х0,5. Составим уравнения: х 2 +х–1=2х–1 или х 2 +х–1=-(2х–1); решая которые, получим

Ответ: .

№4. Найти корни уравнения: _.

Представим данное уравнение в виде: = х 2 – 1, откуда:

х 2 – 1,

х 2 – 1 при х — 1 и х 1.Решая уравнения, получим из первого: х=0 и х=1, из второго: х=-2 и х=1.

№5. Найти целые корни уравнения: = .

Используя определение модуля, прходим к выводу, что равенство возможно, если значения выражений х–х 2 –1 и 2х+3–х 2 равны или противоположны, т.е. данное уравнение равносильно совокупности двух уравнений:

№6. Решить уравнение: =2х 2 –3х+1.

Обозначим выражение 3х-1-2х 2 буквой а. Тогда данное уравнение примет вид: =-а. Исходя из аналитической записи определения модуля, можно сделать вывод, что данное уравнение равносильно неравенству: 3х–1-2х 2 0, решая которое, получим ответ: х0,5 и х1.

Упражнения для самостоятельной работы.

№1.=х 2 + х–20.

№3. =(х–1)(х+1),

№4. х 2 –6+5=0,

№5. х 2 +8=9,

№6.=х 2 –6х+6,

№7. х =-8.

Занятие №4. Решение уравнений, содержащих абсолютную величину, с параметрами.

Рассмотрим пример: решить уравнение с параметром

3–х=.

Построим графики функций у=3–х и у=. График у=3–х фиксирован и от параметра не зависит. График у=получается из графика фукции у=, зависит от параметра а. Поэтому рассмотрим 3 случая:

Этот случай имеет место при а=3. Тогда графики функций совпадают по отрезку АВ и абсцисса любой точки этого луча является решением данного уравнения, т.е. х 3. Видно, что графики функций не пересекаются, т.е. не имеют общих точек. Поэтому уравнение решения не имеет.

Упражнения для самостоятельной работы:

№1.=а,

№2. а=3,

№3. (а–2)=а–2,

№4. а 2 х 2 +а=0.

Занятие №5. Решение линейных неравенств с модулями.

Неравенства, содержащие переменную под знаком модуля, решают различными способами; рассмотрим достаточно простой пример:

>4.

Первый способ: Имеем: >4,

>4,

>2.

Применив метод интервалов, получим: х 4,5.

Третий способ: Выражение 2х–5 может быть неотрицательным или отрицательным. Т.е. имеем совокупность двух систем:

Рассмотрим еще несколько примеров.

Пример №2.Решить неравенство: 2,

Занятие № 6. Решение квадратных неравенств с модулями.

Решим первую систему: из первого неравенства имеем: х1; х2.

из второго: 2х 2 –5х+20, или 0,5х2.

Отметив найденные решения первого и второго неравенств первой системы на координатной прямой, находим пересечение решений.

Т.о. 0,5х1 и х=2. Это решение первой системы.

№8. >.

Занятие № 7. Решение неравенств, содержащих абсолютную величину, с параметрами.

№2. (х–а) 2 >2+5 не имеет решений?

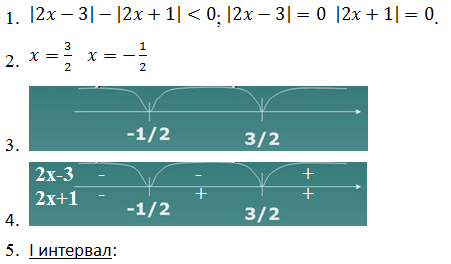
Рассмотрим метод интервалов на примере решения уравнения

—+3-2=х+2.

Чтобы решить данное неравенство, необходимо раскрыть модули. Для этого выделим интервалы, на каждом из которых выражения, стоящие под знаком модуля, принимают только положительные или отрицательные значения. Отыскание таких интервалов основано на теореме: если на интервале (а; в) функция f непрерывна и не обращается в нуль, то она на этом интервале сохраняет постоянный знак.

Чтобы выделить интервалы знакопостоянства, найдем точки, в которых выражения, записанные под модулем, обращаются в нуль:

х+1=0, х=-1; х=0; х–1=0, х=1; х–2=0, х=2.

Полученные точки разобьют прямую на искомые интервалы. Определим знаки выражений

х+1, х, х–1, х–2 на этих интервалах:

Учитывая знаки, раскроем модули. В результате получим совокупность систем, равносильную данному уравнению:

Последняя совокупность приводится к виду:

Использованный прием называется методом интервалов. Он применяется и при решении неравенств.

3) Раскроем модуль:

Решение первой системы: , решение второй . Решение данного неравенства: .

Упражнения для самостоятельной работы:

№1

№2

№3

Рассмотрим неравенства вида и . Примем без доказательства следующую теорему: при любом значении а неравенство равносильно системе неравенств а неравенство равносильно совокупности неравенств

Рассмотрим пример: решить неравенство:>х+2.

Пользуясь сформулированной теоремой, перейдем к совокупности неравенств:

Система и неравенство 0х>2 не имеют решений. Следовательно, решением совокупности (и данного неравенства) является х.

Упражнения для самостоятельной работы:

№1. х+3,

Пример №2. Решите систему уравнений:

Заметим, что Следовательно, по свойству 5 ху0, т.е. х и у принимают значения одного знака. Тогда данная система равносильна совокупности систем:

или

Решением первой системы является любая пара неотрицательных чисел, сумма которых равна 1. Например, (0,5; 0,5), (1/6; 5/6).Решением второй системы является пара неположительных чисел, сумма которых равна – 1. Например, (0,8;-0,2).

Пример №3.Запишите при помощи знака модуля, что по крайней мере одно из чисел а, в, с, d отлично от нуля.

Ответ: