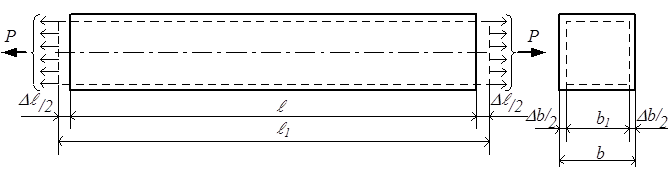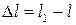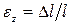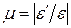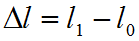Что такое абсолютная продольная деформация
Деформации. Закон Гука



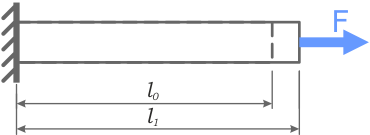
Рассмотрим деформации, возникающие при растяжении и сжатии стержней. При растяжении длина стержня увеличивается, а поперечные размеры сокращаются. При сжатии, наоборот, длина стержня уменьшается, а поперечные размеры увеличиваются. На рис.2.7 пунктиром показан деформированный вид растянутого стержня.
ℓ – длина стержня до приложения нагрузки;
ℓ1 – длина стержня после приложения нагрузки;
b – поперечный размер до приложения нагрузки;
b1 – поперечный размер после приложения нагрузки.
Абсолютная продольная деформация ∆ℓ = ℓ1 – ℓ.
Абсолютная поперечная деформация ∆b = b1 – b.
Значение относительной линейной деформации ε можно определить как отношение абсолютного удлинения ∆ℓ к первоначальной длине бруса ℓ
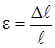
Аналогично находятся поперечные деформации
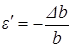
При растяжении поперечные размеры уменьшаются: ε > 0, ε′ 0. Опыт показывает, что при упругих деформациях поперечная всегда прямо пропорциональна продольной.
Коэффициент пропорциональности ν называется коэффициентом Пуассона или коэффициентом поперечной деформации. Он представляет собой абсолютную величину отношения поперечной деформации к продольной при осевом растяжении
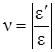
Назван по имени французского учёного, впервые предложившего его в начале XIX века. Коэффициент Пуассона есть величина постоянная для материала в пределах упругих деформаций (т.е. деформаций, исчезающих после снятия нагрузки). Для различных материалов коэффициент Пуассона изменяется в пределах 0 ≤ ν ≤ 0,5: для стали ν = 0,28…0,32; для резины ν = 0,5; для пробки ν = 0.
Между напряжениями и упругими деформациями существует зависимость, известная под названием закон Гука:
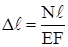
Произведение EF называется жёсткостью бруса при растяжении и сжатии.
Формулы (2.9) и (2.10) – это разные формы записи закона Гука, предложенного в середине XVII века. Современная форма записи этого фундаментального закона физики появилась гораздо позже – в начале XIX века.
Формула (2.10) справедлива лишь в пределах тех участков, где сила N и жёсткость EF постоянны. Для ступенчатого стержня и стержня, нагруженного несколькими силами, удлинения подсчитываются по участкам с постоянными N и F и результаты суммируются алгебраически
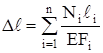
Если эти величины изменяются по непрерывному закону, ∆ℓ вычисляется по формуле
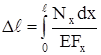
В ряде случаев для обеспечения нормальной работы машин и сооружений размеры их деталей должны быть выбраны так, чтобы кроме условия прочности обеспечивалось условие жёсткости
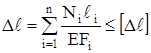
где ∆ℓ – изменение размеров детали;
[∆ℓ] – допускаемая величина этого изменения.
Подчёркиваем, что расчет на жёсткость всегда дополняет расчёт на прочность.
2.4. Расчёт стержня с учетом собственного веса
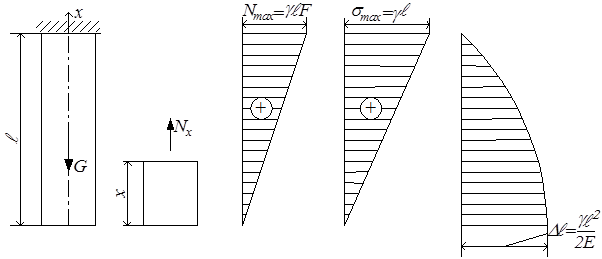
Простейшим примером задачи о растяжении стержня с переменными по длине параметрами является задача о растяжении призматического стержня под действием собственного веса (рис.2.8,а). Продольная сила Nx в поперечном сечении этого бруса (на расстоянии x от его нижнего конца) равна силе тяжести нижележащей части бруса (рис.2.8,б), т.е.
где γ – объёмный вес материала стержня.
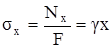
Продольная сила и напряжения меняются по линейному закону, достигая максимума в заделке. Осевое перемещение произвольного сечения равно удлинению вышерасположенной части бруса. Поэтому определить его нужно по формуле (2.12), интегрирование вести от текущего значения х до х = ℓ:
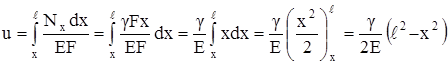
Получили выражение для произвольного сечения стержня
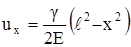
При х = ℓ перемещение наибольшее, оно равно удлинению стержня
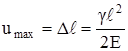
На рис.2.8,в,г,д приведены графики Nx, σх и ux
Умножим числитель и знаменатель формулы (2.17) на F и получим:
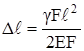
Выражение γFℓ равно собственному весу стержня G. Поэтому
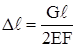
Формула (2.18) может быть сразу получена из (2.10)., если помнить, что равнодействующая собственного веса G должна быть приложена в центре тяжести стержня и поэтому она вызывает удлинение только верхней половины стержня (рис.2.8,а).
Если стержни, кроме собственного веса, нагружены ещё сосредоточенными продольными силами, то напряжения и деформации определяют на основе принципа независимости действия сил отдельно от сосредоточенных сил и от собственного веса, после чего результаты складывают.
Принцип независимости действия сил вытекает из линейной деформируемости упругих тел. Суть его заключается в том, что любая величина (напряжение, перемещение, деформация) от действия группы сил может быть получена как сумма величин, найденных от каждой силы в отдельности.
Коэффициент Пуассона. Связь продольной и поперечной деформации
Пусть в результате деформации первоначальная длина стержня l станет равной. l1. Изменение длины
называется абсолютным удлинением стержня.
При растяжении продольная деформация считается положительной, а при сжатии – отрицательной.
Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются. Если материал является изотропным, то его поперечные деформации равны между собой:
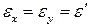
Опытным путем установлено, что при растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной является постоянной для данного материала величиной. Модуль отношения поперечной деформации к продольной, называемый коэффициентом Пуассона или коэффициентом поперечной деформации, вычисляется по формуле:
Для различных материалов коэффициент Пуассона изменяется в пределах 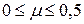
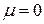
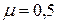
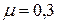
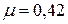
абсолютная деформация
Полезное
Смотреть что такое «абсолютная деформация» в других словарях:
абсолютная деформация — Разность между конеч. и нач. значениями величины, характериз. размеры или форму деформир. тела (напр., при растяж. цилиндрич. образца: /к /0 или /j Ff, где /0 и F0 — длина и пл. попереч. сечения образца до испытания, а /к и Ff —… … Справочник технического переводчика
деформация — деформация: Искажение формы куска мыла по сравнению с предусмотренной в техническом документе. Источник: ГОСТ 28546 2002: Мыло туалетное твердое. Общие технические условия оригинал документа Де … Словарь-справочник терминов нормативно-технической документации
Деформация — [deformation; strain] (от лат. deformatio искажение) 1. Изменение размеров и/или формы тела, вызанное взаимным смещением его частиц под влиянием механической нагрузки и других воздействий (термических, электрических, магнитных и др.). Деформация… … Энциклопедический словарь по металлургии
деформация при максимальном усилии sM: Абсолютная — 3.2 деформация при максимальном усилии sM: Абсолютная деформация в направлении удара в центре испытуемого образца, соответствующая максимальному усилию. Для материалов, имеющих на диаграмме «усилие деформация» плоский участок максимального усилия … Словарь-справочник терминов нормативно-технической документации
деформация при разрушении, sp: Абсолютная — 3.6 деформация при разрушении, sp: Абсолютная деформация в направлении удара в центре испытуемого образца, измеренная в точке разрушения (рисунки 1 и 2). Источник … Словарь-справочник терминов нормативно-технической документации
абсолютная линейная деформация — Деформация, измеряемая как разность между конечным и исходным расстояниями между рассматриваемыми точками деформированного объекта. [http://sl3d.ru/o slovare.html] Тематики машиностроение в целом … Справочник технического переводчика
абсолютная угловая деформация — Угловая деформация, измеряемая как разность между исходным прямым углом и конечным углом между двумя отрезками, проходящими через рассматриваемую точку деформированного объекта. [http://sl3d.ru/o slovare.html] Тематики машиностроение в целом … Справочник технического переводчика
ДЕФОРМАЦИЯ — (Deformation) изменение формы (размеров) тела под влиянием внешних сил. Чистая Д. не сопровождающаяся изменением объема тела. Абсолютная Д. разность между двумя значениями одного и того же размера в данном теле после Д. и первоначального.… … Морской словарь
ДЕФОРМАЦИЯ АБСОЛЮТНАЯ — [absolute deformation] разность между конечым и начальным значениями величины, характеризующей размеры или форму деформируемого тела (например, при растяжении цилиндрического образца … Металлургический словарь
холодная деформация — [cold deformation] пластическая деформация, при которой происходит упрочнение и отсутствует разупрочнение. Если деформационное упрочнение сопровождеформация возвратом, то говорят о неполной холодной деформации или теплой деформации. Деформацию… … Энциклопедический словарь по металлургии
Абсолютная деформация при растяжении
Абсолютными называют деформации определяемые величиной изменения соответствующего размера либо положения сечения.
Нагляднее всего абсолютную деформацию можно показать на примере растяжения-сжатия.
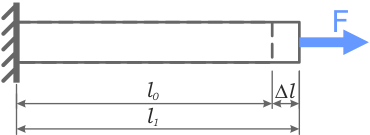
После приложения к стержню продольной растягивающей силы F его длина увеличится до некоторого значения l 1.
Разность между конечным и начальным продольными размерами стержня есть одна из его его абсолютных деформаций при растяжении.
Единица измерения абсолютных деформаций:
Отношение величины абсолютных деформаций к соответствующим начальным размерам тела называют относительными деформациями.
10.3. Простейшие виды нагружения и простейшие конструктивные элементы
    Для отдельно взятого элемента конструкции взаимоуравновешенные активная сила и сила реакции опоры являются внешними силами.
    Рассмотрим, каким образом конструкция оказывает сопротивление внешней нагрузке, за счет чего происходит изменение формы и размеров конструкции – деформирование (от лат. deformatio – искажение).
    Не обращая внимание на то, каким образом, с точки зрения конструктивного решения, приложены внешние силы Р, рассмотрим растяжение элемента конструкции, схема нагружения которого показана на рис. 10.3,а.
 |
Рис. 10.3. Упрощенная модель деформации при растяжении
На рис. 10.3 показана также упрощенная модель межатомных связей в твердом теле. Жесткие и прочные межатомные связи, соединяющие атомы недеформированного тела (рис. 10.3,б), при растяжении (рис. 10.3,в) создают большие внутренние силы противодействия внешней нагрузке, стремящиеся сохранить тело как единое целое.
    Под действием внешних сил частицы (атомы) материала, из которого сделана конструкция, будут перемещаться, и перемещение частиц под нагрузкой будет продолжаться, пока между внешними и внутренними силами не установится равновесие.
    Такое состояние называется деформированным состоянием тела .
    Мерой воздействия внешних сил на атомы вещества, которые удаляются друг от друга (при растяжении) или сближаются (при сжатии), т. е. мерой противодействия материала конструкции внешнему силовому воздействию, мерой внутренних сил в материале является напряжение. Напряжением называется внутренняя сила (возникающая при воздействии внешней нагрузки), приходящаяся на единицу площади в окрестности данной точки рассматриваемого сечения тела:
    В инженерной практике иногда измеряют напряжения в даН/мм 2 (1даН= 10Н).
   Напряжение, таким образом, показывает интенсивность противодействия внутренних сил воздействию внешней нагрузки на межатомные связи материала конструкции, или, что то же самое, интенсивность воздействия внешней нагрузки на межатомные связи.
   Если рассмотреть деформированное состояние стержня (бруса) (рис. 10.4) при растяжении внешними силами Р (показаны на рисунке черными стрелками), то в любом произвольно взятом поперечном сечении (например, плоскостью А) распределение нормальных напряжений σ = Р/F будет равномерным.
 |
Рис. 10.4. Деформированное состояние бруса
| где    | ε |    - | относительное удлинение при растяжении; | |
| ε′ |    - | относительные поперечные деформации.    При достаточно больших внешних нагрузках (и, как следствие, больших внутренних напряжениях) межатомные связи материала могут быть разорваны, что приведет к разрушению конструкции.
Рис. 10.5. Диаграмма растяжения    Прямолинейные на некотором протяжении диаграммы участки (0-А, 0-АВ) характеризуют такую стадию деформирования образца, когда при увеличении нагрузки деформации пропорциональны напряжениям и при снятии нагрузки исчезают, т. е. образец за счет межатомных связей (сил упругости) возвращается в исходное (недеформированное) состояние. На этом участке материал «подчиняется» закону Гука (по имени английского естествоиспытателя Р. Гука): | ||
| ε |    - | относительное удлинение. |
    Модуль упругости Е (наклон кривой деформирования в зоне упругости 0-А (0-АВ) диаграммы: Е = tgα) является мерой упругости («жесткости») и характеризует податливость (способность к деформированию) под нагрузкой. Отметим, что сталь – более жесткий, менее податливый материал, чем алюминиевый сплав.
   Точка А (АВ) на диаграммах характеризует наибольшую нагрузку Рпц и, соответственно, напряжения предела пропорциональности σпц, при которых еще соблюдается линейная зависимость σ – ε.
    Дальше, за точкой А (АВ), линейная зависимость σ – ε нарушается, материал деформируется («течет») под нагрузкой и при снятии нагрузки не возвращается к исходному состоянию, в нем возникают остаточные пластические деформации за счет того, что часть межатомных связей разрушается. Точка В на диаграммах характеризует нагрузку Рт и, соответственно, напряжения предела текучести σт, при которых материал «течет» без увеличения нагрузки. Некоторые материалы (например, 4, см. рис. 10.5) имеют явно выраженную площадку текучести А-В, где деформации существенно увеличиваются без увеличения внешней нагрузки. Для других материалов (1, 2, 3) площадки текучести отсутствуют, в этом случае точки А и В на диаграмме практически совпадают.
   Зона В-С диаграммы называется зоной упрочнения . Здесь после стадии текучести материал снова приобретает способность увеличивать сопротивление дальнейшей деформации, однако для удлинения образца в этой зоне требуется в сотни раз более медленное нарастание нагрузки, чем в зоне упругих деформаций.
 |
Рис. 10.6. Диаграмма истинных напряжений
   Точка С диаграммы характеризует максимальную (предельную) нагрузку Рmax и, соответственно, напряжения предела прочности или напряжения временного сопротивления σв, при которых еще сохраняется целостность элемента конструкции, нагруженного растяжением.
   Дальше, за точкой С диаграммы, без увеличения внешней нагрузки идет лавинообразное разрушение межатомных связей материала.
   Напряжение σв, таким образом, характеризует прочность материала на разрыв.
   Точка D диаграммы характеризует разрушение (разрыв) образца. Нисходящая ветвь диаграммы С-D имеет условный характер, поскольку напряжения рассчитываются для площади поперечного сечения исходного образца. Реально напряжения растут, ч то показывает диаграмма истинных напряжений (рис. 10.6 – пунктирная линия), в которой напряжения рассчитываются для истинной площади поперечного сечения образца. В интервале О-А рост напряжения идет без разрушения межатомных связей, после снятия нагрузки образец возвращается к исходному состоянию. В интервале А-D рост напряжения происходит за счет разрушения межатомных связей и значительного местного утонения образца (образования шейки 1). В момент разрушения (точка D диаграммы) площадь поперечного сечения пластически деформированного образца меньше исходной.
   Прочность конструкции, естественно, зависит от прочности материала, из которого она изготовлена.
    Прочность ( несущая способность ) конструкции – это способность конструкции в определенных условиях воспринимать (выдерживать) без разрушения внешние нагрузки. Нагрузка , при которой происходит разрушение конструкции, называется разрушающей .