Что такое абсолютная погрешность приближенного значения

Приложение А. Погрешности вычислений

Абсолютная и относительная погрешности

Точность полученного в результате вычисления результата определяется погрешностью вычислений. Различают два вида погрешностей – абсолютную и относительную.

Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения:

(А.1)

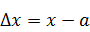
где а – приближенное значение числа х.

Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа:

(А.2)

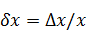
Истинное значение величины х обычно неизвестно. Имеется лишь приближенное значение а и нужно найти его предельную погрешность . В дальнейшем значение принимается в качестве абсолютной погрешности приближенного числа а. Тогда истинное значение х находится в интервале .

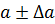
Источники погрешностей

Рассмотрим различные причины возникновения погрешностей.

Математическая модель задачи является неточной

Погрешность возникает из-за того, что сам численный метод или математическая модель является лишь приближением к точному методу (например, дифференцирование). Кроме того, любая математическая модель или метод могут внести существенные погрешности, если в ней не учтены какие-то особенности рассматриваемой задачи. Модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других. Такую погрешность называют также методической. Она всегда имеет место, даже при абсолютно точных данных и абсолютно точных вычислениях. В большинстве случаев погрешность численного метода можно уменьшить до требуемого значения за счет изменения параметров метода (например, уменьшением шага дискретизации, или увеличением количества итераций).

Ошибки в исходных данных

Исходные данные задачи часто являются основным источником погрешностей. Ошибки такого типа неизбежны и проявляются в любых реальных задачах, поскольку любое измерение может быть проведено с только какой-то предельной точностью. Вместе с погрешностями, вносимыми математической моделью, их называют неустранимыми погрешностями, поскольку они не могут быть уменьшены ни до начала решения задачи, ни в процессе ее решения.

Следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности. Сильное уточнение одних исходных данных при наличии больших погрешностей в других не приводит к повышению точности конечных результатов. Если какие-то отдельные точки данных (измерения) явно ошибочные, их можно исключить из вычислений.

Вычислительные ошибки (ошибки округления)

Ошибки этого типа проявляются из-за дискретной (а не непрерывной) формы представления величин в компьютере. Вычислительные ошибки можно свести к минимуму продуманно организовывая алгоритмы.

Вычислительные ошибки

Рассмотрим подробнее вычислительные ошибки. Допустим, исходные данные не имеют погрешности, но поскольку место в памяти компьютера, отведенное на хранение чисел, ограничено, и соответственно ограничена точность представления чисел, возникновение вычислительных ошибок неизбежно.

Представление чисел с плавающей точкой

Для хранения целых чисел (int, long, unsigned int и т.д.) обычно отводится 4 байта памяти, что позволяет представлять целые числа, находящиеся примерно в диапазоне от .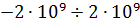

В вычислениях чаще используются вещественные числа (float, double). Такие числа представляются в компьютере в форме с плавающей точкой, и хранятся в логарифмическом виде – мантисса и порядок:

(А.3)

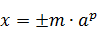
где m – мантисса, p – порядок, а – основание степени.

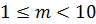
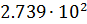
Например, число 273.9 можно представить в виде или в компьютерном представлении 2.739E+02.

В таблице А.1 приводится диапазон допустимых значений и другие параметры для чисел с плавающей точкой одинарной (float) и двойной (double) точности.

Таблица A.1. Диапазон чисел, представимых в формате с плавающей точкой

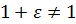
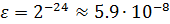
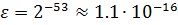
Для чисел с плавающей точкой существует понятие машинного эпсилон – наименьшего положительного число ε такого, что . Например, для числа с одинарной точностью 1 + 0.00000001 = 1. Для одинарной точности , а для двойной точности .

Погрешность округления

При вычислениях с помощью компьютера неизбежны погрешности округлений, связанные с ограниченностью хранимых разрядов мантиссы. Для приближенного числа, полученного в результате округления, абсолютная погрешность принимается равной половине единицы последнего разряда числа. Например, значение могло быть получено округлением чисел 0.73441, 0.73353 и др. При этом . При простом отбрасывании лишних разрядов эта погрешность увеличивается вдвое.

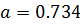
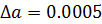
Перевод чисел из одной системы счисления в другую также может быть источником погрешности из-за того, что основание одной системы счисления не является степенью основания другой (например, 10 и 2). Это может привести к тому, что в новой системе счисления число невозможно представить абсолютно точно, например:

Погрешность арифметических действий над приближенными числами

При выполнении операций над приближенными числами можно оценить предельную погрешность результата в зависимости от выполняемой операции. При умножении или делении чисел друг на друга их относительные погрешности складываются:

, (А.4)

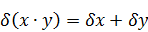
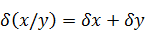
При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени:

(А.5)

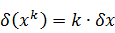
При сложении или вычитании чисел их абсолютные погрешности складываются:

(А.6)

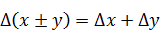
Относительная погрешность суммы положительных слагаемых вычисляется как:

. (А.7)

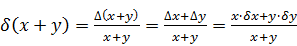
Отсюда следует, что относительная погрешность суммы нескольких чисел одного и того же знака, заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:

. (А.8)

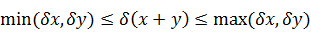
На практике для оценки погрешности при сложении чисел обычно используют максимальную погрешность .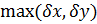

При сложении погрешность будет сильно завесить от абсолютных величин складываемых чисел. Рассмотрим пример сложения двух чисел с одинаковым количеством значащих цифр, но разных по абсолютному значению:

1234 + 0.005678 = 1234.00005678

или в компьютерном представлении:

1.234Е+03 + 5.678Е-03 = 1.234005678Е+03

После сложения количество значащих цифр равно 10. Число с одинарной точностью (float) позволяет хранить только 8 значащих цифр, то есть на самом деле число будет равно 1.2340056Е+03. Две значащие цифры потерялись в процессе сложения. Потеря точности здесь возникает из-за того, что при прибавлении к большому числу малых чисел результат сложения выходит за пределы точности при округлении. Для того чтобы уменьшить погрешность вычислений, нужно складывать числа в порядке возрастания их абсолютной величины. Таким образом можно минимизировать абсолютную величину промежуточной погрешности при каждом сложении.

Рассмотрим теперь вычитание чисел (сложение чисел разного знака, или вычитание чисел одного знака). В соответствии с выражением (А.7) относительная погрешность может быть очень большой в случае, если числа близки между собой, так как даже при малых погрешностях 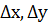результат их сложения в знаменателе может быть очень малым. Чтобы уменьшить погрешность при вычитании, необходимо строить вычислительные алгоритмы таким образом, чтобы избегать вычитания близких чисел.

Таким образом, можно сделать вывод, что сложение и вычисление являются плохо обусловленными (неустойчивыми) операторами, так как при некоторых данных даже небольшая погрешность в исходных данных может привести к большой погрешности результата. Уменьшить погрешность можно за счет правильной последовательности операций. Из-за погрешности округления в машинной арифметике важен порядок выполнения операций, и известные из алгебры законы коммутативности (и дистрибутивности) здесь не всегда выполняются.

Источник

Приближённые вычисления в математике

Содержание:

Приближённые вычисления

Приближённые вычисления — вычисления, в которых данные и результат (или только результат) являются числами, приближенно представляющими истинные значения соответствующих величин. Числовые данные, полученные измерением реальных объектов, редко бывают точными значениями соответствующей величины, а обычно имеют некоторую погрешность

Абсолютная и относительная погрешности

При решении практических задач часто приходится иметь дело с приближёнными значениями разных числовых величин. К ним относятся: результаты измерения разных величин с помощью приборов; значения полученные при считывании на графиках, диаграммах, номограммах; проектные данные; результаты округления чисел; результаты действий над приближёнными числами; табличные значения некоторых величин; результаты вычислений значений функции. Приближённые значения (приближение, приближённые числа) могут значительно отличаться от точных, либо быть близкими к ним.

Для оценки отклонения приближённых чисел от точных используют такие понятия как абсолютная и относительная погрешности.

Абсолютной погрешностью приближённой называется модуль разности между точным значением величины и её приближённым значением х, то есть

Пример.

Абсолютная погрешность приближённого числа числом 0,44 составляет

Если точное число неизвестно, то найти абсолютную погрешность невозможно. На практике вводят оценку допустимой при данных измерениях или вычислениях абсолютной погрешности, которую называют пределом абсолютной погрешности и обозначают буквой h. Считают, что h. Как правило, предел абсолютной погрешности устанавливают из практических соображений, например, при измерениях пределом абсолютной погрешности считают наименьшее деление прибора.

При записи приближённых чисел часто используют понятия верной и сомнительной цифры.

Цифра называется верной, если предел абсолютной погрешности данного приближения не превышает единицы того разряда, в котором записана эта цифра. В другом случае цифра называется сомнительной.

Например: в числе две цифры верны, поскольку погрешность 0,04 не превышает единицу разряда десятых. Цифры 9 и 7 верны, поскольку а цифры 4 и 6 являются сомнительными, поскольку

В конечной записи приближённого числа сохраняют только верные цифры. Так число можно записать в виде , число в виде Если в десятичной дроби последние верные цифры — нули, то их оставляют в записи числа.

Например: если , то правильной записью числа будет 0,260.

Если в целом числе последние нули являются сомнительными, их исключают из записи числа.

Именно поэтому при работе с приближёнными числами широко используют стандартную форму записи числа.

Например: в числе верными являются три первые цифры, а два последних нуля — сомнительные цифры. Запись числа возможна только в виде:

Следовательно, в десятичной записи приближённого числа последняя цифра указывает на точность приближённости, то есть предел абсолютной погрешности не превышает единицу последнего разряда.

Например:

1. Запись означает, что , то есть предел абсолютной погрешности h=0,01.

2. Запись

3. Если

В десятичной записи числа значимыми цифрами называются все его верные цифры начиная с первой слева, отличной от нуля.

Например: в числе 1,13 — три значимых цифры, в числе 0,017 — две, в числе 0,303 — три, в числе 5,200 — четыре, в числе 25_*10 3 — две значимых цифры.

При таком подходе к записи приближенного числа необходимо уметь округлять числа.

Правила округления чисел:

— Если первая цифра, которую отбрасываем является меньше пяти, то в основном разряде, который сохраняется цифра не меняется. Например: 879,673≈879,67.

— Если первая цифра, которую отбрасываем больше пяти, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 456,87≈456,9.

— Если первая цифра, которая отбрасывается пять и за ней есть ещё отличны от нуля, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 1246,5002≈1247.

— Если первая цифра, которая отбрасывается — пять и за ней нет больше никаких цифра, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 0,275≈0,28; 1,865≈1,86.

Абсолютная погрешность не полностью характеризует точность приближения. Например, будет грубой ошибкой при измерении жука, и незначительной при измерении кита. Тоже самое можно сказать и про предел абсолютной погрешности. Качество (точность) приближённости лучше характеризуется относительной погрешностью.

Относительной погрешностью (омега) приближённости х величины называется отношением абсолютной погрешности этого приближения к модулю приближённого значения х, то есть

Поскольку абсолютная погрешность обычно бывает неизвестна, то на практике оценивают модуль относительной погрешности некоторым числом, которое не меньше чем этот модуль:

Число называется пределом относительной погрешности.

Предел относительной погрешности можно вычислить по формуле:

Конечно относительная погрешность выражается в процентах.

С помощью относительной погрешности легко установить точность приближённости.

Пример 1. Найти относительную погрешность числа

Решение: Имеем

Следовательно

Пример 2. Сравнить точность измерения толщины книги d (см) и высоты стола H (см), если известно, что .

Решение:

Как видим, точность измерения высоты стола значительно выше.

Выполнение действий над приближёнными числами

Результат арифметических действий над приближёнными числами является также приближённым числом.

Пример 3. Вычислить приближение значения выражения и найти предел погрешностей результата.

Решение: находим значение квадрата числа 5,62 и квадратного корня из числа 18,50.

Найдём границу относительной погрешности результата:

Граница абсолютной погрешности результата:

Ответ:

Пример 4. Вычислить приближение значения выражения и найти предел погрешностей результата.

Решение: находим значение квадратного корня из числа 6,24 и , имеем:

Граница относительной погрешности результата:

Граница абсолютной погрешности результата:

Ответ:

Выполнение действий без точного учёта погрешности

Точный учёт погрешности усложняет вычисление. Поэтому, если не надо учитывать погрешность промежуточных результатов, можно использовать более простые правила.

Сложение и вычитание приближённых вычислений рекомендуется выполнять так:

а) выделить слагаемое с наименьшим числом верных десятичных знаков;

б) округлить другие слагаемые так, чтобы каждое из них содержало на один десятичный знак больше чем выделенное;

в) выполнить действия, учитывая все сохранённые десятичные знаки;

г) результаты округлить и сохранить столько десятичных знаков, сколько их есть в приближённом числе с наименьшим числом десятичных знаков.

Умножение и деление приближённых вычислений рекомендуется выполнять так:

а) выделить среди данных чисел, число с наименьшим количеством верных значимых цифр;

б) округлить оставшиеся данные так, чтобы каждое из них содержало на одну значащую цифру больше, чем в выделенном;

в) выполнить действия — сохранить все значимые цифры;

г) сохранять в результате столько значащих цифр, сколько их имеет выделенное число с наименьшим количеством верных значимых цифр.

При возведении в степень приближённого числа в результате сохраняют столько значимых цифр, сколько верных значимых цифр имеет основа степени.

При извлечении корня из приближённого числа в результате сохраняют столько верных цифр, сколько имеет подкоренное число.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник