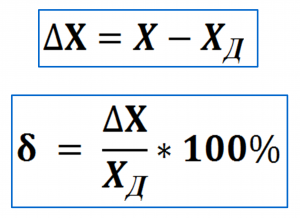Что такое абсолютная и относительная погрешность измерения электротехника
Погрешности измерений
Общие сведения об измерениях. Погрешности измерений и средств измерений
Общие сведения об измерениях
Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств. Под измерением понимается процесс экспериментального сравнения данной физической величины с однородной физической величиной, значение которой принято за единицу.
Мера – средство измерений, предназначенное для воспроизведения физической величины заданного размера.
Измерительный прибор – средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем. Измерительные приборы классифицируются по различным признакам. Например, измерительные приборы можно построить на основе аналоговой схемотехники или цифровой. Соответственно их делят на аналоговые и цифровые. Ряд приборов, выпускаемых промышленностью, допускают только отсчитывание показаний. Эти приборы называются показывающими. Измерительные приборы, в которых предусмотрена регистрация показаний, носят название регистрирующих.
Погрешности измерений
Погрешность является одной из основных характеристик средств измерений.
Под погрешностью электроизмерительных приборов, измерительных преобразователей и измерительных систем понимается отклонение их выходного сигнала от истинного значения входного сигнала.
Абсолютная погрешность Δa прибора есть разность между показанием прибора ах и истинным значением а измеряемой величины, т.е.
Абсолютная погрешность, взятая с обратным знаком, называется поправкой.
Относительная погрешность δ представляет собой отношение абсолютной погрешности к истинному значению измеряемой величины. Относительная погрешность, обычно выражаемая в процентах, равна
Приведенная погрешность γП есть выраженное в процентах отношение абсолютной погрешности Δa к нормирующему значению апр
Нормирующее значение – условно принятое значение, могущее быть равным конечному значению диапазона измерений (предельному значению шкалы прибора).
Погрешности средств измерений
Класс точности прибора указывают просто числом предпочтительного рода, например, 0,05. Это используют для измерительных приборов, у которых предел допускаемой приведенной погрешности постоянен на всех отметках рабочей части его шкалы (присутствует только аддитивная погрешность). Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой.
Класс точности прибора (например, амперметра) дается выражением
При установлении классов точности приборов нормируется приведенная погрешность, а не относительная. Причина этого заключается в том, что относительная погрешность по мере уменьшения значений измеряемой величины увеличивается.
По ГОСТ 8.401-80 в качестве значений класса точности прибора используется отвлеченное положительное число из ряда:
В интервале от 1 до 100 можно использовать в качестве значений класса точности числа:
(α = 0) 1; 1,5; 2; 2,5; 4; 5; 6;
(α = 1) 10; 15; 20; 25; 40; 50; 60.
Т.е. четырнадцать чисел 1; 1,5; 2; 2,5; 4; 5; 6; 10; 15; 20; 25; 40; 50; 60.
Необходимо отметить, классы точности от 6,0 и выше считаются очень низкими.
Примеры решения задач
Задача №1
Определить для вольтметра с пределом измерения 30 В класса точности 0,5 относительную погрешность для точек 5, 10, 15, 20, 25 и 30 В и наибольшую абсолютную погрешность прибора.
Решение
Приведенная погрешность (выраженное в процентах отношение абсолютной погрешности к нормирующему значению)
постоянна и равна классу точности прибора.
Относительная погрешность однократного измерения (выраженное в процентах отношение абсолютной погрешности к истинному значению измеряемой величины)
уменьшается к значению класса точности прибора с ростом измеренного значения к предельному значению шкалы прибора.
Абсолютная погрешность однократного измерения
постоянна на всех отметках рабочей части шкалы прибора.
По условию задачи: Uизм = Ui = 5, 10, 15, 20, 25 и 30 В – измеренное значение электрической величины; Uпр = 30 В – предел шкалы вольтметра.
Погрешности электрических измерений



Показание приборов всегда отличаются от действительных значений измеряемой величины. Оценка точности показаний определяется различными видами погрешности.
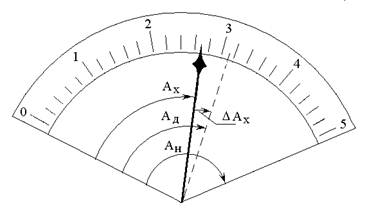
Абсолютная погрешность ∆Аx
Абсолютная погрешность ∆Ах показания прибора равна разности между показанием прибора Ах и действительным значением измеряемой величины Ад (рис.1-3)
Основные величины на шкале:
Величина абсолютной погрешности в разных точках шкалы равная, она может быть и положительной, и отрицательной. Чем меньше абсолютная погрешность, тем достовернее результаты измерения.
Относительная погрешность- γх
Более общей и хорошо сопоставимой характеристикой измерения является относительная погрешность.
Относительная погрешность измерения равна отношению абсолютной погрешности измеряемой величины Ах к ее действительному значению Ад, выраженному в процентах (рис.1-3).
так как Ад и Ах мало отличаются друг от друга.
Относительная приведенная погрешность-γпр
Погрешность самих приборов характеризуется величиной, называемой относительной приведенной погрешностью γпр.
Класс точности прибора равен максимальному значению приведенной погрешности (1.3).
Согласно ГОСТу электроизмерительные приборы подразделяются на восемь классов точности (табл. 1-3).
| Класс точности прибора | 0,05 | 0,1 | 0,2 | 0,5 | 1,5 | 2,5 | ||
| Колебание допустимой погрешности | ±0,05% | ±0,1% | ±0,2% | ±0,5% | ±1% | ±1,5% | ±2,5% | ±4% |
Пример. Вольтметром класса 1,0 с номинальным значением Uн=250В измеряют напряжение U1=50В и U2=200В.
В первом случае погрешность измерения будет:
Поэтому для повышения точности измерения следует пользоваться приборами, у которых измеряемая величина отсчитывалась бы во второй половине шкалы. Это позволяет осуществлять измерения с погрешностью, не превышающей удвоенного значения класса точности прибора.
Виды и методы измерения электрических величин
Измерение – это сравнения физической величины, которая измеряется, с некоторым значением такой же величины, принятым за единицу. Они измеряются специальными устройствами — средствами измерения. Поскольку не все приборы обладают абсолютно одинаковыми характеристиками существуют различные методы измерений, методы оценки измерений, а также погрешности при измерениях.
Измерения проводят прямым и косвенным путем
Прямые –это когда нужное значение измеряемой величины определяется по шкале (дисплею) прибора.
К таким относятся измерение электроэнергии счетчиком, напряжения и тока – амперметром и вольтметром соответственно и пр.
Косвенное — искомое значение нужной величины находят на основании аналитической зависимости (например формулы) между необходимой величиной и величинами, полученными при помощи прямых измерений. То есть эти измерения позволяют сократить количество проводимых измерений, а вычислить нужные значения с помощью формул. Например, 
Измерения могут проводится различными способами и, соответственно, средствами. Соответственно такие измерения нужно оценить, для этого существуют методы непосредственной оценки и методы сравнения.
Методы непосредственной оценки и методы сравнения
Непосредственная оценка. При применении данного метода значение нужной величины вычисляют по шкале прибора (тока — по амперметру, напряжения — по вольтметру и пр.). Он довольно прост, но не отличается сравнительно высокой точностью.
Сравнения. Состоит в том, что величина, которая измеряться, сравнивается с величиной, воспроизводимой мерой. Он обеспечивает точность, большую, чем метод непосредственной оценки, но процесс измерения значительно усложняется. У метода сравнения есть несколько разновидностей: дифференциальной, нулевой и замещения.
При нулевом методе стараются свести влияние на измерительное устройство измеряемых величин до нуля. Пример — с помощью уравновешенного моста для измерения электрического сопротивления.
При методе замещения величину которая подлежит измерению замещают известной величиной, которая воспроизводится мерой. При этом, изменяя известную величину, добиваются точно такого же показания прибора, как и то, которое действовало при действии измеряемой величины. Таким образом устанавливают погрешность. При использовании дифференциального метода разность между величиной и измеряемой величиной, воспроизводимой мерой действуют на измерительный прибор. Пример — с помощью неуравновешенного моста измерение электрического сопротивления.
Известно, что приборов с точностью абсолютной не существует в мире, то каждый прибор характеризуется погрешностью. Они делятся на относительные, абсолютные и приведенные.
Погрешность абсолютная А — это разность между фактическим значением шкалы прибора А и действительным значением измеряемой величины АД:
Погрешность относительная — это отношение погрешности абсолютной ∆ к фактическому значению измеряемой величины А. Выражается она в процентах:
Погрешность приведенная — представляет собой ничто иное как отношение абсолютной погрешности ∆ к нормирующему значению АN измеряемой величины:
Обычно нормирующее значение принято принимать равным верхнему пределу измерения для прибора.
Погрешности бывают: систематические и случайные
Погрешность систематическая. Она остается постоянной, но может и меняться по любому, но определенному закону. Значение ее всегда учитывается путем введения соответствующих поправок, для минимизации влияние погрешностей.
Погрешность случайная.Она появляется непредсказуемо и изменяется по случайному закону. Их нельзя исключить, но можно систематизировать и минимизировать их влияние произведя несколько измерений.
Также на появление погрешностей производит влияние и условия эксплуатации приборов. Поэтому, погрешности могут быть двух видов: основная и дополнительная.
Погрешность основная. Она появляется на измерительных приборах, которые находятся в нормальных условиях эксплуатации (атмосферное давление, влажность, температура внешней среды, напряжение и пр.).
Погрешность дополнительная. Она происходит тогда, когда устройство не эксплуатируется в нормальных условиях.
Уровень точности приборов характеризуется классом точности. Для электроизмерительных приборов установлены такие классы точности как: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5 и 4.
Цифры эти указывают указывают основную приведенную погрешность γ, которая показывается в процентах. Абсолютная ∆ и относительная δ погрешности могут быть представлены в таком виде:
Из данной статьи можно сделать вывод, что при измерении электрических величин следует учитывать класс точности прибора и условия окружающей среды. Для более высокой точности измерений необходимо использовати различные методы измерений. Для исключения влияния случайных факторов нужно провести одно и тоже измерение несколько раз.
Погрешности измерений
Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.
Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).
В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».
Содержание
Определение погрешности
В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.
Классификация погрешностей
По форме представления
где Xtrue — истинное значение, а Xmeas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина Xmeas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.
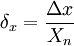
— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то Xn определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.
По причине возникновения
В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.
Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.
Терминология: Погрешности измерений физических величин
При выборе измерительного оборудования всегда стоит типичная задача – количественно описать задачу измерения: что нужно измерять и с какой точностью? Вопрос о реально требуемой точности измерений всегда является ключевым вопросом, определяющим цену оборудования, поскольку эта цена (цена полного технического решения) резко зависит от требуемой точности измерений.
Физические величины и погрешности их измерений
Задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью.
Сразу оговоримся, что при выборе измерительного оборудования часто нужно также знать диапазон измерения и какое именно значение интересует: например, среднеквадратическое значение (СКЗ) измеряемой величины в определённом интервале времени, или требуется измерять среднеквадратическое отклонение (СКО) (для измерения переменной составляющей величины), или требуется измерять мгновенное (пиковое) значение. При измерении переменных физических величин (например, напряжение переменного тока) требуется знать динамические характеристики измеряемой физической величины: диапазон частот или максимальную скорость изменения физической величины. Эти данные, необходимые при выборе измерительного оборудования, зависят от физического смысла задачи измерения в конкретном физическом эксперименте.
Итак, повторимся: задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Эта задача решается с помощью прямых или косвенных измерений.
При прямом измерении осуществляется количественное сравнение физической величины с соответствующим эталоном при помощи измерительных приборов. Отсчет по шкале прибора указывает непосредственно измеряемое значение. Например, термометр дает значения измеряемой температуры, а вольтметр – значение напряжения.
При косвенных измерениях интересующая нас физическая величина находится при помощи математических операций над непосредственно измеренными физическими величинами (непосредственно измеряя напряжение U на резисторе и ток I через него, вычисляем значение сопротивления R = U / I ).
Точность прямых измерений некоторой величины X оценивается величиной погрешности или ошибки, измерений относительно действительного значения физической величины XД.
Действительное значение величины XД (согласно РМГ 29-99) – это значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
Различают абсолютную (∆X) и относительную (δ) погрешности измерений.
Относительная погрешность измерения – это п огрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному значению измеряемой величины. Обычно относительную погрешность выражают в процентах: δ = (∆X / Xд) * 100%.
При оценке точности косвенных измерений некоторой величины X1, функционально связанной с физическими величинами X2, X3,…, X1 = F (X2, X3, …), учитывают погрешности прямых измерений каждой из величин X2, X3,… и характер функциональной зависимости F (). Приводим ниже примеры вычисления погрешности косвенного измерения для четырёх наиболее типичных функциональных зависимостей.
| Характер функциональной зависимости F () | Абсолютная погрешность косвенного измерения физической величины X1 | |
|---|---|---|
| X1= X2+ X3 | ∆X1= ∆X2+ ∆X3 | δ = ( ∆X2+ ∆X3 ) / (X2+ X3) |
| X1= X2– X3 | ∆X1= ∆X2+ ∆X3 | δ = ( ∆X2+ ∆X3 ) / (X2– X3) |
| X1= X2* X3 | ∆X1=X3*∆X2+ X2*∆X3 | δ = (∆X2/X2) + (∆X3/X3) |
| X1= X2 / X3 | ∆X1=(X3*∆X2+ X2*∆X3)/(X3) 2 | δ = (∆X2/X2) + (∆X3/X3) |
Приведём краткое определение некоторых других погрешностей средств измерений, согласно РМГ 29-99: