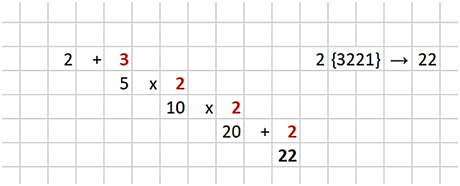Что такое а22 по информатике
Что такое а22 по информатике
Ниже на пяти языках программирования записан алгоритм. Получив на вход число x, этот алгоритм печатает число M. Известно, что x > 100. Укажите наименьшее такое (т. е. большее 100) число x, при вводе которого алгоритм печатает 26.
DIM X, L, M AS INTEGER
IF L MOD 2 = 0 THEN
if L mod 2 = 0 then
using namespace std;
В теле цикла числа M и L уменьшаются, пока не станут равными. Чтобы в итоге было напечатано 26, оба числа в какой-то момент должны быть равны 26. Пойдем от конца к началу: на предыдущем шаге одно число было 26, а другое 26 + 26 = 52. Еще на шаг раньше 52 + 26 = 78 и 52. До того 78 + 52 = 130 и 52. То есть наименьшее возможное число 130. А поскольку найденное число четное, то M будет присвоено значение 52, что и приведет к необходимому результату.
Ниже на пяти языках программирования записан алгоритм. Получив на вход число x, этот алгоритм печатает число M. Известно, что x > 100. Укажите наименьшее такое (т. е. большее 100) число x, при вводе которого алгоритм печатает 30.
DIM X, L, M AS INTEGER
using namespace std;
В теле цикла числа M и L уменьшаются, пока не станут равными. Чтобы в итоге было напечатано 30, оба числа в какой-то момент должны быть равны 30. Пойдем от конца к началу: на предыдущем шаге одно число было 30, а другое 30 + 30 = 60. Еще на шаг раньше 60 + 30 = 90 и 30. До того 90 + 30 = 120 и 90. То есть наименьшее возможное число 120.
Ниже на пяти языках программирования записан алгоритм. Получив на вход число N, этот алгоритм печатает число q. Укажите наименьшее из таких чисел N, при вводе которых алгоритм напечатает 17.
Разбор задания №22 ЕГЭ-2019 по информатике и ИКТ
Демоверсия КИМ ЕГЭ-2019 по информатике не претерпела никаких изменений по своей структуре по сравнению с 2018 годом. Это значимо упрощает работу педагога и, конечно, уже выстроенный (хочется на это рассчитывать) план подготовки к экзамену обучающегося.
Мы рассмотрим решение предлагаемого проекта (на момент написания статьи – пока еще проекта) КИМ ЕГЭ по информатике.
Часть 1
Ответами к заданиям 1–23 являются число, последовательность букв или цифр, которые следует записать в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания, начиная с первой клеточки, без пробелов, запятых и других дополнительных символов. Каждый символ пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами.
Задание 22
Исполнитель Вычислитель преобразует число, записанное на экране. У исполнителя есть три команды, которым присвоены номера:
Первая из них увеличивает число на экране на 2, вторая умножает его на 2, третья увеличивает его на 3.
Программа для Вычислителя – это последовательность команд.
Сколько существует таких программ, которые преобразуют исходное число 2 в число 22 и при этом траектория вычислений программы содержит число 11?
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 123 при исходном числе 7 траектория будет состоять из чисел 9, 18, 21.
Решение
Для начала решим задачу просто, без учета дополнительного условия «содержит число 11»:
Программа короткая, а также она не дает в своей траектории вычисления значения 11. И тут стоит разбить задачу на две небольшие задачи: определить число путей от 2 до 11 и от 11 до 22. Итоговый результат, очевидно, будет соответствовать произведению этих двух значений. Построение сложных схем с деревьями – нерациональная трата времени на экзамене. Чисел в нашем диапазоне не так много, поэтому предлагаю рассмотреть следующий алгоритм:
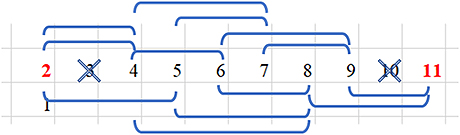
Выпишем все числа от стартового и до последнего включительно. Под первым напишем 1. Двигаясь слева направо, рассмотрим число способов попадания в текущую позицию, используя данные нам команды.
Сразу можно убрать очевидные позиции, не влияющие на решение: 3 можно зачеркнуть – понятно, что в нее нельзя попасть из стартовой позиции, используя одну из доступных нам команд; 10 – через нее мы не можем никак попасть в нашу промежуточную, а главное, обязательную позицию 11.
В 4 мы можем попасть двумя путями-командами: х2 и +2, т.е. через 4 проходят 2 пути. Напишем это значение под 4. В 5 можно попасть единственным способом: +3. Напишем под 5 значение 1. В 6 можно попасть единственным путем – через 4. А под ней у нас указано значение 2. Соответственно, именно по этим двум путям, проходя 4, мы попадем из 2 в 6. Пишем под 6 значение 2. В 7 можно попасть из двух предыдущих позиций, используя имеющиеся у нас команды, и для получения числа путей, которые нам доступны для попадания в 7, мы сложим числа, которые указывали под этими предыдущими позициями. Т.е. в 7 мы попадаем 2 (из-под 4) + 1 (из-под 5) = 3 путями. Действуя по этой схеме и далее, получаем:
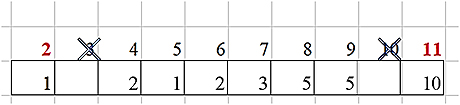
Перейдем в правую половину от условного центра – 11. Только теперь при расчете будем учитывать только те пути, которые проходят через этот центр.
Двигаясь и далее слева направо, мы получаем искомый результат – 100.
Ответ: 100.
Заместитель генерального директора по ИКТ АНОО «Дом знаний», преподаватель по программированию Яндекс.Лицея (ДГУНХ, Махачкала), учитель высшей категории, финалист Всероссийского конкурса «Учитель года России 2010»
Задание 22 ЕГЭ по информатике
Примеры решения типовых задач задания 22 ЕГЭ по информатике. Задание 22 является заданием повышенного уровня сложности. Обобщение опыта преподавания данного материала.
Просмотр содержимого документа
«Задание 22 ЕГЭ по информатике»
Задание 22 ЕГЭ по информатике
Условие задачи сводятся к тому, что существует некий исполнитель, который умеет выполнять несколько команд (система команд исполнителя – СКИ). Необходимо найти количество программ, преобразующих число А в число В.
Задание 22 претерпело изменения на протяжении нескольких лет присутствия в КИМ ЕГЭ по информатике.
На данный момент задачи можно разделить на несколько групп:
Задачи без ограничения условий (приведенный выше вариант).
Задачи с ограничением первого типа: траектория прохождения содержит число N.
Задачи с ограничением второго типа: траектория вычислений не содержит число M.
Задачи с ограничением первого и второго типов: траектория прохождения содержит число N и не содержит число M.
На своих уроках все эти типы задач я стараюсь разобрать на одном примере. Просто так получается быстрее, так как часть задачи уже решена, и нагляднее. Я не претендую на свою методику решения данных задач, а просто хочу обобщить свой опыт, который, надеюсь, может кому-то пригодится. При подготовке учащихся к сдаче ЕГЭ пользуюсь материалами сайта К.Ю. Полякова.
Исполнитель Счетчик преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
Первая команда увеличивает число на экране на 2, вторая умножает его на 2. Программа для исполнителя Счетчик это последовательность команд.
Сколько существует программ, для которых при исходном числе 2 результатом является число 44 и при этом траектория вычислений содержит число 18 и не содержит числа 34?
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 4 траектория будет состоять из чисел 6, 12, 14.
KN – количество разных программ для получения числа N из начального числа.
Построим рекуррентную формулу, связывающую KN с предыдущими элементами последовательности K1, K2, K3,…, KN-1, то есть с решениями таких же задач для меньших N.
Число N могло быть получено одной из двух операций:
увеличением на 2 числа N-2;
увеличением в 2 раза числа N/2.
Я задаю одну рекуррентную формулу и для четных и для нечетных чисел, т.к. можно считать, что для чисел нечетных KN/2 = 0. То же самое можно сказать и про KN при N меньших начального числа (KN = 0).
В нашем примере нечетные числа мы вообще получить не можем.
Будем решать данную задачу в несколько этапов, рассматривая следующие варианты:
2 – 44, не содержит 34
2 – 44, содержит 18 и не содержит 34.
На самом деле, это 4 разных задачи. Просто их удобно рассматривать вместе.
По рекуррентной формуле имеем:
Задача 2: 2 – 44, содержит 18
Эта задача разбивается на две задачи: 2 – 18 и 18 – 44.
Первая у нас уже решена выше. Мы можем получить число 18 десятью способами.
Дальше мы решаем вторую задачу: 18 – 44, считая, что всех предыдущих вычислений не было. Т.е. все KN для N
Задача 3: 2 – 44, не содержит 34
В э той задаче траектория не может проходить через число 34, поэтому считаем, что K34 = 0 Дальше вычисления ведем обычным способом.
Использую первую задачу, получим:
Задача 4: 2 – 44, содержит 18 и не содержит 34
Мы рассмотрели все 4 варианта данной задачи.
В 2017 году в задании 22 появился еще один тип задач. В условие задачи говорится о том, что предпоследней командой является какая-то определенная команда из СКИ.
Следующую задачу я взяла с сайта К.Ю. Полякова. Задача № 51, задание 22.
Исполнитель Калькулятор преобразует целое число, записанное на экране. У исполнителя две команды, каждой команде присвоен номер:
Первая команда увеличивает число на экране на 1, вторая увеличивает это число в 2 раза. Сколько существует программ, которые число 5 преобразуют в число 32 и в которых предпоследняя команда 1?
Если две последние команды «11», то до выполнения этих команд у нас было число 32 – 1 – 1 = 30. Это значит, что нам нужно получить количество команд преобразующих 5 в 30.
Если две последние команды «12», то до выполнения этих команд у нас было число 32/2 – 1 = 15. Это значит, что нам нужно получить количество команд преобразующих 5 в 15.
Число N могло быть получено одной из двух операций:
увеличением на 1 числа N-1;
умножением на 2 числа N/2 (только для четных N)
Если N нечетное, то считаем, что KN/2 = 0.
Далее решаем задачу обычным способом: 5 – 30
Разбор демоверсии ЕГЭ по информатике 2022 (22-27 Задание)
Продолжаем анализ демонстрационного варианта ЕГЭ по информатике 2022.
В этой статье разберём с 22-ого по 27 задание.
ЕГЭ по информатике 2022 будет повержено!
Ниже на четырёх языках программирования записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: L и M. Укажите наибольшее число x, при вводе которого алгоритм печатает сначала 4, а потом 5.
Решение данного задания будет похоже на решение 6 задания из ЕГЭ по информатике 2022.
С помощью перебора на языке Python найдём при каких значениях переменная L=4 И переменная M=5 в конце программы.
Наибольшее значение равно 49.
Исполнитель преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
Программа для исполнителя – это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 20, и при этом траектория вычислений содержит число 10?
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17.
Решим задачу c помощью шаблона на языке Python.
Если число x достигло пункта назначения, то возвращаем 1. Если оно перескочило y, то возвращаем 0. А если ещё не дошло до y, то продолжаем вычисления с помощью рекурсии.
У нас число 10 обязательное, поэтому разбиваем функцию следующим образом F(1, 10)*F(10, 20), через умножение. Это и будет ответ. Получается 28.
Текстовый файл состоит из символов P, Q, R и S.
Определите максимальное количество идущих подряд символов в прилагаемом файле, среди которых нет идущих подряд символов P. Для выполнения этого задания следует написать программу.
Напишем решение на языке Python.
Подсчитываем символы, пока не встретилась комбинация двух P подряд. Как только встретилась данная комбинация, сбрасываем счётчик на 1. Здесь мы сбрасываем счётчик на значение 1, чтобы учесть один символ, которые находится в самой комбинации PP. И в начале мы тоже устанавливаем счётчик в значение 1 по этой же причине.
Мы проходим в цикле for до длины строки минус один. Значение 1 в счётчике при сбросе и в начале программы так же компенсирует и тот момент, что мы не подсчитываем последний символ!
При изменении счётчика, сохраняем максимальное значение в переменной mx
Если бы у нас была вместо PP другая комбинация, состоящая к примеру из 5 символов, то мы бы тогда в начале и при сбросе писали в счётчик значение 5-1=4.
В этой задаче получается ответ 188.
Пусть M – сумма минимального и максимального натуральных делителей целого числа, не считая единицы и самого числа. Если таких делителей у числа нет, то значение M считается равным нулю.
Напишите программу, которая перебирает целые числа, бо́льшие 700 000, в порядке возрастания и ищет среди них такие, для которых значение M оканчивается на 8. Выведите первые пять найденных чисел и соответствующие им значения M.
Формат вывода: для каждого из пяти таких найденных чисел в отдельной строке сначала выводится само число, затем – значение М. Строки выводятся в порядке возрастания найденных чисел.
Количество строк в таблице для ответа избыточно.
На ЕГЭ по информатике 2022 удобно писать программы на языке Python.
В данной программе перебираются числа в цикле for, начиная с 700001.
Переменная b-считается наибольшим делителем числа i. Затем, с помощью ещё одного цикла for перебираются числа с 2 до корня числа i (включительно). Ищем тем самым наименьший делитель.
Если до корня числа включительно не встретился ни один делитель, значит, у числа нет делителей, кроме 1 и самого числа.
Пусть у нас есть число A. Если у этого числа есть делитель d1, то он находится до корня этого числа. А вот то число (так же делитель), на которое умножается это число d1, чтобы получить A, будет находиться после корня A.
Таким образом, первый найденный делитель будет являться наименьшим делителем. А вот делительный, который находится в паре с наименьшим делителем, будет наибольшим.
После того, как мы нашли наименьший делитель (он будет сидеть в переменной j) и наибольший делитель b, выходим из второго цикла for.
Если переменная b осталась равна нулю, то, значит, у числа i нет указанных делителей, и переменная M должна равняться 0. Если b не равна нулю, то M=j+b.
Проверить, на что оканчивается число, можно узнав остаток от деления числа на 10.
Переменная count следит, чтобы было распечатано ровно 5 чисел, которые удовлетворяют условию задачи.
Ответ:
| 700005 | 233338 |
| 700007 | 100008 |
| 700012 | 350008 |
| 700015 | 140008 |
| 700031 | 24168 |
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов.
Известно, какой объём занимает файл каждого пользователя.
По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
В первой строке входного файла находятся два числа: S – размер свободного места на диске (натуральное число, не превышающее 10 000) и N – количество пользователей (натуральное число, не превышающее 1000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое – в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем – максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Пример входного файла:
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов – 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар – 50, поэтому ответ для приведённого примера:
Решим задачу с помощью Excel. Чтобы открыть текстовый файл в программе Excel, выбираем Файл->Открыть, выбираем нужную папку и указываем, чтобы в папке были видны все типы файлов.
И выбираем наш текстовый файл.
Выскочит окно Мастер текстов (импорт). Здесь оставляем выбранный пункт с разделителями и кликаем Далее.
В следующем окне поставим ещё галочку пробел. В итоге Символами-разделителем будут знак табуляции и пробел.
Кликаем ещё раз Далее и Готово.
Наши данные вставятся, как нужно!
Число 8200 (размер свободного места) нужно запомнить или записать на черновике. Число 970 (количество файлов) нам в принципе не нужно при таком подходе решения.
1. Найдём максимальное количество файлов.
Выделяем весь столбец A и сортируем его по возрастанию.
Теперь выделяем ячейки сверху мышкой, а справа в нижней части программы будет показываться сумма выделенных ячеек.
Мы должны выделить максимальное количество ячеек, но чтобы сумма не превышала число 8200.
Получается максимальное количество файлов, которое можно сохранить, равно 568.
2. Найдём максимальный размер файла при максимальном количестве файлов.
Если мы сохраним максимальное количество файлов, то у нас ещё останется свободное место 8200-8176=24, т.к. сумма выделенных ячеек равна 8176.
Мы можем заменить наибольший файл (последняя выделенная ячейка равная 29) ещё большим файлом, размер которого не превышает 24+29=53.
Если покрутим таблицу вниз, то найдём такой файл размером 50. Это и будет наибольший файл при максимальном количестве файлов.
Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, такие что сумма элементов каждой из них кратна k = 43. Найдите среди них подпоследовательность с максимальной суммой, определите её длину. Если таких подпоследовательностей найдено несколько, в ответе укажите количество элементов самой короткой из них.
Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество чисел N (1 ≤ N ≤ 10 000 000). Каждая из следующих N строк содержит одно натуральное число, не превышающее 10 000.
Пример организации исходных данных во входном файле:
В ответе укажите два числа: сначала значение искомой суммы для файла А, затем – для файла B.
Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Напишем программу на Python.
Тогда кандидатом для ответа будет цепочка, которая получается, если от цепочки с суммой s «отрезать» цепочку с суммой из массив sum_ost, которая соответствует текущему остатку (переменная ost).
В массив sum_ost для каждого остатка записывается сумма только один раз, т.к. нам нужна именно минимальная сумма для каждого остатка, чтобы кандидат для ответа был как можно больше.
В начале массив sum_ost инициализируется очень большим числом 1096594666. Это число больше, чем сумма всех элементов в файле. Оно было найдено до основного решения, с помощью простой программы.
В процессе решения мы ищем среди кандидатов для ответа цепочку с максимальной суммой. Делаем это стандартным образом: кто больше, то и победил. Мы инициализируем большими числом 1096594666 элементы массива sum_ost для того, чтобы условие нормально сработало, когда в массиве sum_ost ещё нет суммы для данного остатка.
Так же мы сохраняем индексы элементов в массив k, когда записываем суммы для различных остатков в массив sum_ost. Это делается для того, чтобы можно было вычислить длину цепочки.
Разбор 2 задания ЕГЭ по информатике
Объяснение задания 2 ЕГЭ по информатике
2-е задание: «Таблицы истинности»
Уровень сложности — базовый,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 3 минуты.
Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы
«Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению»
Таблицы истинности и порядок выполнения логических операций
Таблица истинности операции НЕ
Таблица истинности операции И (конъюнкция)
Таблица истинности операции ИЛИ (дизъюнкция)
Таблица истинности операции Импликация (если…, то…)
Таблица истинности операции Эквивалентность (тогда и только тогда, …)
О преобразованиях логических операций читайте здесь.
Решение заданий 2 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube: 
Логическая функция F задается выражением
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| . | . | . | . | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
print(‘x y z w’) for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (not(x) or y or z) and (x or not(z) or not(w)) if not(F): print(x, y, z, w)
Язык pascalAbc.net:
begin writeln(‘x’:7, ‘y’:7, ‘z’:7,’w’:7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not x or y or z) and (x or not z or not w)) then writeln(x:7, y:7, z:7,w:7); end.
Ответ:
Результат: xwzy
🎦 Видео решения 169 задания К.Полякова (бескомпьютерный вариант):
Миша заполнял таблицу истинности функции:
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)
но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| . | . | . | . | F |
| 1 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.
Результат: ywxz
✎ Способ 2. Программирование:
begin writeln(‘x’:7, ‘y’:7, ‘z’:7,’w’:7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not z and (x xor y)) false = 0, True = 1
Сопоставив их с исходной таблицей, получим результат: ywxz
print (‘x y z w’) for x in 0,1: for y in 0,1: for z in 0,1: for w in 0,1: F=(not z and not(x==y)) F=0 :
Сопоставив их с исходной таблицей, получим результат:
Результат: ywxz
🎦 Доступно видео решения этого задания (бескомпьютерный вариант):
🎦 Видео (решение 2 ЕГЭ в Excel):
Логическая функция F задается выражением
¬a ∧ b ∧ (c ∨ ¬d)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| . | . | . | . | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
Результат: cbad
🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| . | . | . | . | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
✍ Решение:
Результат: xzwy
✎ Способ 2. Программирование:
Язык pascalABC.NET:
begin writeln(‘x ‘,’y ‘,’z ‘,’w ‘); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not(not x or y or(not z and w)) then writeln(x:7,y:7,z:7,w:7); end.
🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
Логическая функция F задаётся выражением
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| . | . | . | . | F |
| 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 |
Результат: xwzy
🎦 Видеорешение (бескомпьютерный вариант):
Задания для тренировки
Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.
Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?
✍ Решение:
Результат: 31
Подробное объяснение данного задания смотрите на видео:
Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.
Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?
✍ Решение:
Результат: 8
Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.
Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?
✍ Решение:
Результат: 256
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
✍ Решение:
Результат: 1
Решение 2 задания ГВЭ по информатике смотрите на видео:
Дано логическое выражение, зависящее от 5 логических переменных:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Сколько существует различных наборов значений переменных, при которых выражение истинно?
✍ Решение:
Теперь рассмотрим каждый случай отдельно:
¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.
Результат: 2
Подробное решение задания смотрите в видеоуроке:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.
✍ Решение:
Результат: 62
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 0 | 0 | |||||
| 0 | 0 | 1 | |||||
| 1 | 1 | 1 |
Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
✍ Решение:
Результат: 4
В видеоуроке рассмотрено подробное решение 2 задания:
Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| . | . | . | F | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
Результат: yzx
Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео: