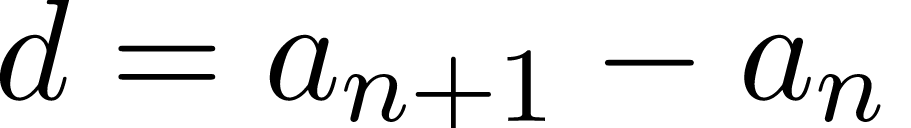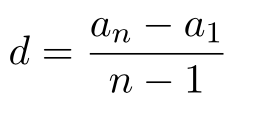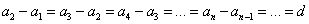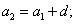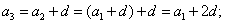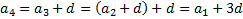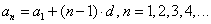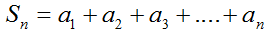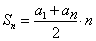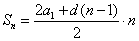Что такое а энное в арифметической прогрессии

20.04.202227.04.2022 admin 0 Comments

Что такое а энное в арифметической прогрессии

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )

Оч-ч-чень полезная формула! Позволяет быстро и легко решать самые разнообразные задания по арифметической прогрессии. Имеет смысл освоить, правда?) Вот она, эта формула:

В чём главная суть формулы?

Эта формула позволяет найти любой член арифметической прогрессии ПО ЕГО НОМЕРУ » n» .

Разумеется, надо знать ещё первый член a₁ и разность прогрессии d, ну так без этих параметров конкретную прогрессию и не запишешь.

Итак, разберёмся с формулой n-го члена арифметической прогрессии.

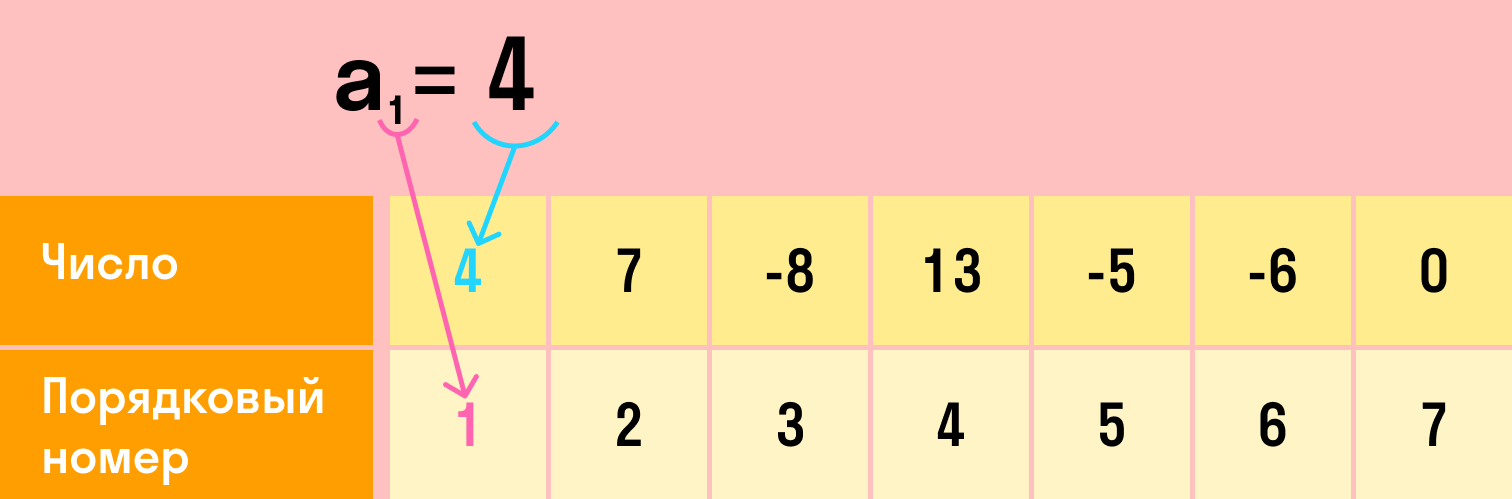
Прогрессию в общем виде можно записать в виде ряда чисел:

А как обозначить в общем виде любой член арифметической прогрессии, с любым номером? Очень просто! Вот так:

Это и есть n-й член арифметической прогрессии. Под буквой n скрываются сразу все номера членов: 1, 2, 3, 4, и так далее.

И что нам даёт такая запись? Подумаешь, вместо цифры буковку записали.

Эта запись даёт нам мощный инструмент для работы с арифметической прогрессией. Используя обозначение a_n, мы можем быстро найти любой член любой арифметической прогрессии. И ещё кучу задач по прогрессии решить. Сами дальше увидите.

В формуле n-го члена арифметической прогрессии:

Формула связывает ключевые параметры любой прогрессии: a_n; a₁; d и n. Вокруг этих параметров и крутятся все задачки по прогрессии.

Формула n-го члена может использоваться и для записи конкретной прогрессии. Например, в задаче может быть сказано, что прогрессия задана условием:

Такая задачка может и в тупик поставить. Нет ни ряда, ни разности. Но, сравнивая условие с формулой, легко сообразить, что в этой прогрессии a₁=5, а d=2.

А бывает ещё злее!) Если взять то же условие: a_n = 5 + (n-1)·2, да раскрыть скобки и привести подобные? Получим новую формулу:

Чаще всего обозначение a_n+1 встречается в рекуррентных формулах. Не пугайтесь этого страшного слова!) Это просто способ выражения члена арифметической прогрессии через предыдущий. Допустим, нам дана арифметическая прогрессия вот в таком виде, с помощью рекуррентной формулы:

Посчитать третий член можно через второй:

В арифметической прогрессии рекуррентную формулу легко превратить в обычную. Посчитать пару последовательных членов, вычислить разность d, найти, если надо, первый член a₁, записать формулу в обычном виде, да и работать с ней. В ГИА подобные задания частенько встречаются.

Применение формулы n-го члена арифметической прогрессии.

Для начала рассмотрим прямое применение формулы. В конце предыдущего урока была задачка:

Дана арифметическая прогрессия (a_n). Найти a₁₂₁, если a₁=3, а d=1/6.

Эту задачку можно безо всяких формул решить, просто исходя из смысла арифметической прогрессии. Прибавлять, да прибавлять. Часок-другой.)

А по формуле решение займёт меньше минуты. Можете засекать время.) Решаем.

В условиях приведены все данные для использования формулы: a₁=3, d=1/6. Остаётся сообразить, чему равно n. Не вопрос! Нам надо найти a₁₂₁. Вот и пишем:

Прошу обратить внимание! Вместо индекса n появилось конкретное число: 121. Что вполне логично.) Нас интересует член арифметической прогрессии номер сто двадцать один. Вот это и будет наше n. Именно это значение n = 121 мы и подставим дальше в формулу, в скобки. Подставляем все числа в формулу и считаем:

Вот и все дела. Так же быстро можно было бы найти и пятьсот десятый член, и тысяча третий, любой. Ставим вместо n нужный номер в индексе у буквы «a» и в скобках, да и считаем.

Напомню суть: эта формула позволяет найти любой член арифметической прогрессии ПО ЕГО НОМЕРУ » n» .

Решим задание похитрее. Пусть нам попалась такая задачка:

Найдите первый член арифметической прогрессии (a_n), если a₁₇=-2; d=-0,5.

Если возникли затруднения, подскажу первый шаг. Запишите формулу n-го члена арифметической прогрессии! Да-да. Руками запишите, прямо в тетрадке:

А теперь, глядя на буквы формулы, соображаем, какие данные у нас есть, а чего не хватает? Имеется d=-0,5, имеется семнадцатый член. Всё? Если считаете, что всё, то задачу не решите, да.

У нас ещё имеется номер n! В условии a₁₇=-2 спрятаны два параметра. Это и значение семнадцатого члена (-2), и его номер (17). Т.е. n=17. Эта «мелочь» часто проскакивает мимо головы, а без неё, (без «мелочи», а не головы!) задачу не решить. Хотя. и без головы тоже.)

Теперь можно просто тупо подставить наши данные в формулу:

Вот, в сущности, и всё. Осталось выразить первый член арифметической прогрессии из формулы, да посчитать. Получится ответ: a₁= 6.

Ещё одна популярная задачка:

Найдите разность арифметической прогрессии (a_n), если a₁=2; a₁₅=12.

Что делаем? Вы удивитесь, пишем формулу!)

Соображаем, что нам известно: a₁=2; a₁₅=12; и (специально выделю!) n=15. Смело подставляем в формулу:

Это правильный ответ.

Так, задачи на a_n, a₁ и d порешали. Осталось научиться номер находить:

Число 99 является членом арифметической прогрессии (a_n), где a₁=12; d=3. Найти номер этого члена.

Подставляем в формулу n-го члена известные нам величины:

Выражаем из формулы n, считаем. Получим ответ: n=30.

А теперь задачка на ту же тему, но более творческая):

Определите, будет ли число 117 членом арифметической прогрессии (a_n):

Так, самое простое сделали. Осталось разобраться с неизвестным номером n и непонятным числом 117. В предыдущей задачке хоть было известно, что дан именно член прогрессии. А здесь и того не знаем. Как быть!? Ну, как быть, как быть. Включить творческие способности!)

Опять выражаем из формулы n, считаем и получаем:

Опаньки! Номер получился дробный! Сто один с половиной. А дробных номеров в прогрессиях не бывает. Какой вывод сделаем? Да! Число 117 не является членом нашей прогрессии. Оно находится где-то между сто первым и сто вторым членом. Если бы номер получился натуральным, т.е. положительным целым, то число было бы членом прогрессии с найденным номером. А в нашем случае, ответ задачи будет: нет.

Задача на основе реального варианта ГИА:

Арифметическая прогрессия задана условием:

Найти первый и десятый члены прогрессии.

Так же, как и в предыдущих задачах, подставляем n=1 в данную формулу:

Аналогично ищем десятый член:

Спокойствие! Эту формулку легко вывести. Не очень строго, но для уверенности и правильного решения точно хватит!) Для вывода достаточно помнить элементарный смысл арифметической прогрессии и иметь пару-тройку минут времени. Нужно просто нарисовать картинку. Для наглядности.

Рисуем числовую ось и отмечаем на ней первый. второй, третий и т.п. члены. И отмечаем разность d между членами. Вот так:

Смотрим на картинку и соображаем: чему равняется второй член? Второй член равняется первый член плюс одно d:

Чему равняется третий член? Третий член равняется первый член плюс два d.

Улавливаете? Я не зря некоторые слова выделяю жирным шрифтом. Ну ладно, ещё один шаг).

Чему равняется четвёртый член? Четвёртый член равняется первый член плюс три d.

Пора сообразить, что количество промежутков, т.е. d, всегда на один меньше, чем номер искомого члена n. Т.е., до номера n, количество промежутков будет n-1. Стало быть, формула будет (без вариантов!):

Задания для самостоятельного решения.

Что, неохота картинку рисовать?) Ещё бы! Уж лучше по формуле, да.

3. Арифметическая прогрессия задана условием: a₁ =-5,5; a_n+1= a_n+0,5. Найдите сто двадцать пятый член этой прогрессии.

В этом задании прогрессия задана рекуррентным способом. Но считать до сто двадцать пятого члена. Не всем такой подвиг под силу.) Зато формула n-го члена по силам каждому!

4. Дана арифметическая прогрессия (a_n):

Найти номер наименьшего положительного члена прогрессии.

Без формулы пришлось бы считать, да считать. Но формула здорово сокращает время решения и уменьшает количество ошибок. Ну и элемент фантазии должен помочь.)

5. По условию задания 4 найти сумму наименьшего положительного и наибольшего отрицательного членов прогрессии.

Не самая простая задачка, да. ) Здесь способ «на пальцах» не прокатит. Придётся формулы писать да уравнения решать.

Ответы (в беспорядке):

3,7; 3,5; 2,2; 37; 2,7; 56,5

Получилось? Это приятно!)

Не всё получается? Бывает. Кстати, в последнем задании есть один тонкий момент. Внимательность при чтении задачи потребуется. И логика.

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

А вот здесь можно познакомиться с функциями и производными.

Источник

Арифметическая прогрессия: свойства и формулы

Определение числовой последовательности

Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.

Последовательности можно задавать разными способами:

«Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23. »

Последовательность y_n = C называют постоянной или стационарной.

Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: a_n+1 = a_n + a_n-1.

Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.

Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.

Свойства числовых последовательностей:

Возрастающие и убывающие последовательности называют монотонными последовательностями.

Запишем числа, которые первые пришли в голову: 7, 19, 0, −1, −2, −11, 0… Сколько бы чисел не написали, всегда можно сказать, какое из них первое, какое — второе и так до последнего. То есть мы можем их пронумеровать.

Пример числовой последовательности выглядит так:

В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.

N-ный член алгебраической последовательности — это число с порядковым номером n.

Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a₁, a₂. a₁₀. a_n.

N-ый член последовательности можно задать формулой. Например:

Определение арифметической прогрессии

Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.

Рассмотрим основные определения и как найти арифметическую прогрессию.

Арифметическая прогрессия — это числовая последовательность a₁, a₂. a_n. для которой для каждого натурального n выполняется равенство:

a_n+1= a_n + d, где d — это разность арифметической прогрессии.

Описать словами эту формулу можно так: каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же числом d.

Разность между последующим и предыдущим членами, то есть разность арифметической прогрессии можно найти по формуле:

Если известны первый член a₁ и n-ый член прогрессии, разность можно найти так:

Арифметическая прогрессия бывает трех видов:

Пример: последовательность чисел 11, 14, 17, 20, 23. — это возрастающая арифметическая прогрессия, так как ее разность d = 3 > 0.

Свойство арифметической прогрессии

Переведем с языка формул на русский: каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. Что как раз объясняет название «арифметическая» прогрессия.

Формула n-го члена арифметической прогрессии

Из определения арифметической прогрессии следует, что равенство истинно:

Значит,

Переведем с языка формул на русский: если мы знаем первый член и разность арифметической прогрессии, то можем найти любой ее член.

Арифметическую прогрессию можно назвать заданной, если известен ее первый член и разность.

Формулы арифметической прогрессии

В 9 классе проходят все формулы арифметической прогрессии. Давайте узнаем, какими способами ее можно задать:

Сумма первых n членов арифметической прогрессии (а_n) обозначается S_n:

Формулы нахождения суммы n членов арифметической прогрессии:

Чтобы быстрее запомнить формулы можно использовать такую табличку с основными определениями:

Рассмотрим пример арифметической прогрессии.

Дано: арифметическая прогрессия (a_n), где a₁ = 0 и d = 2.

Найти: первые пять членов прогрессии и десятый член прогрессии.

Решение арифметической прогрессии:

По условиям задачи n = 10, подставляем в формулу:

Геометрическая прогрессия

Геометрическая прогрессия — это последовательность (b_n), в которой каждый последующий член можно найти, если предыдущий член умножить на одно и то же число q.

Если последовательность (b_n) является геометрической прогрессией, то для любого натурального значения n справедлива зависимость:

b_n+1 = b_n * q, где q — знаменатель геометрической прогрессии

Если в геометрической прогрессии (b_n) известен первый член b₁ и знаменатель q, то можно найти любой член прогрессии:

Общий член геометрической прогрессии bn можно вычислить при помощи формулы:

Пример 1. 2, 6, 18, 54,… — геометрическая прогрессия b = 2, q = 3.

Пример 3. 7, 7, 7, 7,… — геометрическая прогрессия b = 7, q = 1.

Источник

Арифметическая прогрессия (ЕГЭ 2022)

Знаменитый ученый Карл Гаусс однажды сказал:

«Ничего не сделано, если что-то осталось недоделанным.»

Поэтому давай сейчас разберем одну из важнейших тем алгебры – арифметическую прогрессию.

А если остались какие-то пробелы, заполним их.

Кстати, Гаусса мы вспомнили не просто так 🙂

Арифметическая прогрессия — коротко о главном

Определение арифметической прогрессии:

Арифметическая прогрессия — это числовая последовательность, в которой разница между соседними числами одинакова и равна \( \displaystyle d\).

Арифметическая прогрессия бывает возрастающей (\( \displaystyle d>0\)) и убывающей (\( \displaystyle d Формула нахождения n-ого члена арифметической прогрессии:

Как найти член прогрессии, если известны его соседние члены:

Сумма членов арифметической прогрессии:

Числовая последовательность

Итак, сядем и начнем писать какие-нибудь числа. Например: \( \displaystyle 4,\text< >7,\text< >-8,\text< >13,\text< >-5,\text< >-6,\text< >0,\text< >\ldots \)

Писать можно любые числа, и их может быть сколько угодно (в нашем случае их \( \displaystyle 7\)). Сколько бы чисел мы не написали, мы всегда можем сказать, какое из них первое, какое – второе и так далее до последнего, то есть, можем их пронумеровать.

Это и есть пример числовой последовательности.

Числовая последовательность – это множество чисел, каждому из которых можно присвоить уникальный номер.

Например, для нашей последовательности:

Присвоенный номер характерен только для одного числа последовательности. Иными словами, в последовательности нет трех вторых чисел. Второе число (как и \( \displaystyle n\)-ное число) всегда одно.

Число с номером \( \displaystyle n\) называется \( \displaystyle n\)-ным членом последовательности.

Всю последовательность мы обычно называем какой-нибудь буквой (например, \( \displaystyle a\)), и каждый член этой последовательности – той же буквой с индексом, равным номеру этого члена: \( \displaystyle <_<1>>,\text< ><_<2>>,\text< >…,\text< ><_<10>>,\text< >…,\text< ><_>\).

Арифметическая прогрессия — определения

Допустим, у нас есть числовая последовательность, в которой разница между соседствующими числами одинакова и равна d.

Такая числовая последовательность называется арифметической прогрессией.

Термин «прогрессия» был введен римским автором Боэцием еще в 6 веке и понимался в более широком смысле, как бесконечная числовая последовательность.

Название «арифметическая» было перенесено из теории непрерывных пропорций, которыми занимались древние греки.

Арифметическая прогрессия – это числовая последовательность, каждый член которой равен предыдущему, сложенному с одним и тем же числом. Это число называется разностью арифметической прогрессии и обозначается d.

Попробуй определить, какие числовые последовательности являются арифметической прогрессией, а какие нет:

Разобрался? Сравним наши ответы:

Является арифметической прогрессией – 2, 3.

Не является арифметической прогрессией – 1, 4.

Вернемся к заданной прогрессии (\( \displaystyle 3;\text< >7;\text< >11;\text< >15;\text< >19\ldots \)) и попробуем найти значение ее 6-го члена.

Существует два способа его нахождения.

Нахождения n-ого члена арифметической прогрессии

Способ I

Итак, 6-ой член описанной арифметической прогрессии равен 23.

Способ II

А что если нам нужно было бы найти значение \( \displaystyle 140\)-го члена прогрессии? Суммирование заняло бы у нас не один час, и не факт, что мы не ошиблись бы при сложении чисел.

А теперь очень важно! Чтобы облегчить себе работу, нужно найти закономерность, потом описать ее формулой и потом пользоваться этой формулой, чтобы вычислять в разы быстрее.

Это и есть математика!

Важно научиться находить закономерности, а потом уже запоминать формулы. Потому что, даже если ты забудешь формулу, ты сможешь ее вывести. И, самое главное, ты сможешь проверить подходит та или иная формула для решения задачи, а не просто подставлять их как обезьянка.

Давай попробуем вывести формулу. Это легко и тебе понравится! Чтобы найти закономерности, надо пользоваться тем, что мы знаем.

Чему равен 2-й член арифметической прогрессии? Попробуй сначала написать числами, а потом в более общем виде, заменив числа буквами.

Закономерности пока не видны. Ок. Идем дальше. Чему равен 3-й член арифметической прогрессии?

Похоже что вырисовывается закономерность! Чтобы узнать значение 2-го члена прогрессии, мы прибавляли одно d, а чтобы узнать 3-го — два d! Иными словами, нам надо прибавлять каждый раз на одно d меньше, чем номер члена прогрессии.

Давай проверим? Чему равен 4-й член арифметической прогрессии?

Бинго! Закономерность подтверждается. Теперь осталось описать закономерность формулой и пользоваться ею!

Если нам нужно найти значение числа прогрессии с порядковым номером n, мы прибавляем к первому члену арифметической прогрессии число d, которое на одно значение меньше порядкового номера искомого числа.

А теперь запомни эту формулу и используй ее для быстрого счета. А если забудешь — то легко выведешь.

Например, посмотрим, из чего складывается значение \( \displaystyle 4\)-го члена данной арифметической прогрессии:

Попробуй самостоятельно найти таким способом значение члена \( \displaystyle n=6\) данной арифметической прогрессии.

Рассчитал? Сравни свои записи с ответом:

Обрати внимание, что у тебя получилось точно такое же число, как и в предыдущем способе, когда мы последовательно прибавляли \( \displaystyle d\) к предыдущему значению членов арифметической прогрессии.

Попробуем «обезличить» данную формулу – приведем ее в общий вид и получим:

Кстати, таким образом мы можем посчитать и \( \displaystyle 140\)-ой член данной арифметической прогрессии (да и \( \displaystyle 169\)-ый тоже можем, да и любой другой вычислить совсем несложно).

Попробуй посчитать значения \( \displaystyle 140\)-го и \( \displaystyle 169\)-го членов, применив полученную формулу.

Возрастающие и убывающие арифметические прогрессии

Возрастающие – прогрессии, в которых каждое последующее значение членов больше предыдущего.

Убывающие – прогрессии, в которых каждое последующее значение членов меньше предыдущего.

Выведенная формула применяется в расчете членов как в возрастающих, так и в убывающих членах арифметической прогрессии.

Проверим это на практике.

Нам дана арифметическая прогрессия, состоящая из следующих чисел: \( \displaystyle 13;\text< >8;\text< >4;\text< >0;\text< >-4.\)

Проверим, какое получится \( \displaystyle 4\)-ое число данной арифметической прогрессии, если при его расчете использовать нашу формулу:

Заметим, что так как арифметическая прогрессия убывающая, то значение \( \displaystyle d\) будет отрицательным, ведь каждый последующий член меньше предыдущего.

Таким образом, мы убедились, что формула действует как в убывающей, так и в возрастающей арифметической прогрессии.

Попробуй самостоятельно найти \( \displaystyle 140\)-ой и \( \displaystyle 169\)-ый члены этой арифметической прогрессии.

Сравним полученные результаты:

Свойство арифметической прогрессии (или как найти n-й член прогрессии, зная соседние)

Усложним задачу — выведем свойство арифметической прогрессии.

Допустим, нам дано такое условие:

\( \displaystyle 4;\text< >x;\text< >12\ldots \) — арифметическая прогрессия, найти значение \( \displaystyle x\).

Легко, скажешь ты и начнешь считать по уже известной тебе формуле:

Получается, мы сначала находим \( \displaystyle d\), потом прибавляем его к первому числу и получаем искомое \( \displaystyle x\).

Если прогрессия представлена маленькими значениями, то ничего сложного в этом нет, а если нам в условии даны числа \( \displaystyle 4024;

Согласись, есть вероятность ошибиться в вычислениях.

А теперь подумай, можно ли решить эту задачу в одно действие с использованием какой-либо формулы?

Конечно да, и именно ее мы попробуем сейчас вывести.

Просуммируем предыдущий и последующий члены прогрессии:

Получается, что сумма предыдущего и последующего членов прогрессии – это удвоенное значение члена прогрессии, находящегося между ними.

Иными словами, чтобы найти значение члена прогрессии при известных предыдущих и последовательных значениях, необходимо сложить их и разделить на \( 2\).

Попробуем посчитать значение \( x\), используя выведенную формулу:

Все верно, мы получили это же число. Закрепим материал.

Посчитай значение \( x\) для прогрессии \( \displaystyle 4024;

x;6072\) самостоятельно, ведь это совсем несложно.

Молодец! Ты знаешь о прогрессии почти все!

Осталось узнать только одну формулу, которую по легендам без труда вывел для себя один из величайших математиков всех времен, «король математиков» – Карл Гаусс…

Сумма первых n членов арифметической прогрессии

Когда Карлу Гауссу было 9 лет, учитель, занятый проверкой работ учеников других классов, задал на уроке следующую задачу:

«Сосчитать сумму всех натуральных чисел от \( \displaystyle 1\) до \( \displaystyle 40\) (по другим источникам до \( \displaystyle 100\)) включительно».

Каково же было удивление учителя, когда один из его учеников (это и был Карл Гаусс) через минуту дал правильный ответ на поставленную задачу, при этом, большинство одноклассников смельчака после долгих подсчетов получили неправильный результат…

Юный Карл Гаусс заметил некоторую закономерность, которую без труда заметишь и ты.

Допустим, у нас есть арифметическая прогрессия, состоящая из \( \displaystyle 6\)-ти членов: \( \displaystyle 6;\text< >8;\text< >10;\text< >12;\text< >14;\text< >16…\)

Нам необходимо найти сумму данных \( \displaystyle 6\) членов арифметической прогрессии.

Конечно, мы можем вручную просуммировать все значения, но что делать, если в задании необходимо будет найти сумму \( \displaystyle 100\) ее членов, как это искал Гаусс?

Изобразим заданную нам прогрессию. Присмотрись внимательно к выделенным числам и попробуй произвести с ними различные математические действия.

Попробовал? Что ты заметил? Правильно! Их суммы равны

А теперь ответь, сколько всего наберется таких пар в заданной нам прогрессии?

Конечно, ровно половина всех чисел, то есть \( \frac<6><2>=3\).

Исходя из того, что сумма двух членов арифметической прогрессии равна \( 22\), а подобных равных пар \( 3\), мы получаем, что общая сумма равна:

\( \displaystyle S\text< >=\text< >22\cdot 3\text< >=\text< >66\).

Таким образом, формула для суммы первых \( \displaystyle n\) членов любой арифметической прогрессии будет такой:

В некоторых задачах нам неизвестен \( \displaystyle n\)-й член, но известна разность прогрессии. Попробуй подставить в формулу суммы, формулу \( \displaystyle n\)-го члена. \( <_>=<_<1>>+d\left( n-1 \right)\)

Что у тебя получилось?

Молодец! Теперь вернемся к задаче, которую задали Карлу Гауссу: посчитай самостоятельно, чему равна сумма \( \displaystyle 40\) чисел, начиная от \( \displaystyle 1\)-го, и сумма \( \displaystyle 100\) чисел начиная от \( \displaystyle 1\)-го.

Сколько у тебя получилось?

У Гаусса получилось, что сумма \( \displaystyle 100 \) членов равна \( \displaystyle 5050\), а сумма \( \displaystyle 40 \) членов \( \displaystyle 820\).

На самом деле формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом еще в 3 веке, да и на протяжении всего этого времени остроумные люди вовсю пользовались свойствами арифметической прогрессии.

Например, представь Древний Египет и самую масштабную стройку того времени – строительство пирамиды… На рисунке представлена одна ее сторона.

Где же здесь прогрессия скажешь ты? Посмотри внимательно и найди закономерность в количестве песчаных блоков в каждом ряде стены пирамиды.

Чем не арифметическая прогрессия? Посчитай, сколько всего блоков необходимо для строительства одной стены, если в основание кладется \( \displaystyle 6\) блочных кирпичей.

Надеюсь, ты не будешь считать, водя пальцем по монитору, ты же помнишь последнюю формулу и все, что мы говорили об арифметической прогрессии?

В данном случае прогрессия выглядит следующим образом:

\( \displaystyle 6;\text< >5;\text< >4;\text< >3;\text< >2;\ 1\).

Разность арифметической прогрессии \( \displaystyle

Количество членов арифметической прогрессии \( \displaystyle=6\).

Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).

Разность арифметической прогрессии \( \displaystyle

Количество членов арифметической прогрессии \( \displaystyle=6\).

Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).

Способ 1.

Способ 2.

А теперь можно и на мониторе посчитать: сравни полученные значения с тем количеством блоков, которое есть в нашей пирамиде.

Молодец, ты освоил сумму \( \displaystyle n\)-ных членов арифметической прогрессии.

Конечно, из \( \displaystyle 6\) блоков в основании пирамиду не построишь, а вот из \( \displaystyle 60\)?

Попробуй рассчитать, сколько необходимо песчаных кирпичей, чтобы построить стену с таким условием.

Верный ответ – \( \displaystyle 1830\) блоков:

Источник

Аналитический информационный портал

Что такое а энное в арифметической прогрессии

Что такое а энное в арифметической прогрессии

Применение формулы n-го члена арифметической прогрессии.

Если Вам нравится этот сайт.

Арифметическая прогрессия: свойства и формулы

Определение числовой последовательности

Определение арифметической прогрессии

Свойство арифметической прогрессии

Формула n-го члена арифметической прогрессии

Формулы арифметической прогрессии

Геометрическая прогрессия

Арифметическая прогрессия (ЕГЭ 2022)

Арифметическая прогрессия — коротко о главном

Числовая последовательность

Арифметическая прогрессия — определения

Нахождения n-ого члена арифметической прогрессии

Возрастающие и убывающие арифметические прогрессии

Свойство арифметической прогрессии (или как найти n-й член прогрессии, зная соседние)

Сумма первых n членов арифметической прогрессии

Добавить комментарий Отменить ответ

Что такое а энное в арифметической прогрессии

Применение формулы n-го члена арифметической прогрессии.

Если Вам нравится этот сайт.

Арифметическая прогрессия: свойства и формулы

Определение числовой последовательности

Определение арифметической прогрессии

Свойство арифметической прогрессии

Формула n-го члена арифметической прогрессии

Формулы арифметической прогрессии

Геометрическая прогрессия

Арифметическая прогрессия (ЕГЭ 2022)

Арифметическая прогрессия — коротко о главном

Числовая последовательность

Арифметическая прогрессия — определения

Нахождения n-ого члена арифметической прогрессии

Возрастающие и убывающие арифметические прогрессии

Свойство арифметической прогрессии (или как найти n-й член прогрессии, зная соседние)

Сумма первых n членов арифметической прогрессии

Вам также понравится

Что такое hicare в honor

Что значит понятие обществознание

Что случилось с инстаграммом

Добавить комментарий Отменить ответ