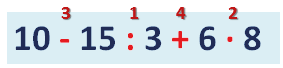
Что сначала умножение или деление в примере со скобками
Зубодробительная задачка с очень простой математикой
Эта задача поставит в тупик половину интернета, но не вас.
Вот вам очень простой математический пример:
8 / 2(2 + 2)
Вы удивитесь, но большинство людей не смогут правильно это посчитать. Посчитайте сами и потом смотрите правильный ответ:
В интернете много споров про такие примеры, поэтому мы решили разобраться, какие ошибки совершают чаще всего и почему многие считают неправильно. Для решения нам понадобятся три математических правила:
Разберём подробнее, что это значит в нашем случае.
1. То, что в скобках, выполняется в первую очередь. То есть в нашем примере, вне зависимости от чего угодно, сначала схлопнутся скобки:
2. Между числом и скобкой можно опустить знак умножения. У нас перед скобкой двойка, то есть можно сделать такую замену:
3. Математические действия при отсутствии скобок выполняются слева направо: как при чтении, сначала умножение и деление, потом — сложение и вычитание. Умножение и деление имеют одинаковый приоритет. Нет такого, что сначала всегда делается умножение, затем деление, или наоборот. Со сложением и вычитанием то же самое.
Некоторые считают, что раз множители были написаны близко друг к другу (когда там стояли скобки), то оно выполняется в первую очередь, ссылаясь при этом на разные методические пособия. На самом деле это не так, и нет такого скрытого умножения, которое имеет приоритет над другим умножением или делением. Это такое же умножение, как и остальные, и оно делается в общем порядке — как и принято во всём математическом мире.
Получается, что нам сначала надо сложить 2 + 2 в скобках, потом 8 разделить на 2, и полученный результат умножить на то, что в скобках:
8 / 2 × (2 + 2) = 8 / 2 × 4 = 4 × 4 = 16
Кстати, если на айфоне записать это выражение точно так же, как в условии, телефон тоже даст правильный ответ.
А инженерный калькулятор на Windows 10 так записывать не умеет и пропускает первую двойку-множитель. Попробуйте сами 🙂
Тут в тред врываются математики и с воплями «Шустеф!» поясняют криком:
«В АЛГЕБРЕ ТОТ ЖЕ ПОРЯДОК ДЕЙСТВИЙ, ЧТО И В АРИФМЕТИКЕ, но есть исключение: в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается. Например, a:b·c= a: (b·c)».
Этот текст из «Методики преподавания алгебры», курс лекций, Шустеф М. Ф., 1967 год. (стр. 43)
Раз в спорном примере знак умножения опущен, то спорный пример алгебраический, а значит, сначала умножаем 2 на 4, а потом 8 делим на 8!

А вот как на это отвечают те, кто действительно в теме и не ленится полностью посмотреть первоисточник:
«Для устранения недоразумений В. Л. Гончаров указывает, что предпочтительнее пользоваться в качестве знака деления чертой и ставить скобки [87]. П. С. Александров и А. Н. Колмогоров [59] предложили изменить порядок действий в арифметике и решать, например, так: 80:20×2=80:40=2 вместо обычного: 80:20×2=4×2=8. Однако это предложение не нашло поддержки».
Если апеллировать к Фриде Максовне Шустеф, то выходит, что:
Самое интересное, что дальше в примерах Фрида Максовна пользуется как раз правильным порядком действий, объясняя решение. Даже там, где есть умножение на скобку с опущенным знаком, она выполняет действия слева направо.

Порядок действий
Для правильного вычисления значений числовых выражений, в которых нужно произвести более одного действия, необходимо знать установленный порядок выполнения арифметических действий.
Порядок действий без скобок
Установленный порядок арифметических действий без скобок:
Порядок действий со скобками
Если выражение содержит скобки, то сначала выполняются все действия внутри скобок, а затем все действия, находящиеся за скобками.
В числовых выражениях со скобками порядок выполнения арифметических действий такой же, как и в выражениях без скобок.
Скобки применяются для обозначения действий, которые нужно произвести раньше остальных. Скобки не влияют на порядок остальных действий в выражении, остальные действия выполняются в указанном порядке.
Дробная черта
Дробная черта в выражении может быть заменена на знак деления, в этом случае, всё что было над и под дробной чертой надо взять в скобки. Например:
Знак деления в выражении можно заменить дробной чертой только в том случае, если это не нарушает порядок действий. Например, выражение:
нельзя заменить на
потому что такая замена нарушит порядок действий в данном выражении.
| 20 : 4(2 + 3) ≠ | 20 | ; |
| 4(2 + 3) |
| 20 | = 20 : (4(2 + 3)). |
| 4(2 + 3) |
Дробная черта в выражении заменяет скобки и означает, что надо вычислить отдельно выражение, стоящее в числителе, и отдельно выражение, стоящее в знаменателе, и первый результат разделить на второй.
Порядок выполнения действий
В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.
1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.
Например,
В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:
Полностью пример записываем так:
Например,
В числовом выражении 3 арифметических действия: деление, умножение и деление.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:
Полностью пример записываем так:
15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2
2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.
Полностью пример записываем так:
3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.
Полностью пример записываем так:
Например,
В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.
Полностью пример записываем так:
42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44
Вывод:
Поделись с друзьями в социальных сетях:
Порядок действий в математике
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные операции в математике
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? — Умножаем, потом складываем.
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Подставляем полученные значения в исходное выражение:
Порядок действий: умножение, деление, и только потом — сложение. Получится:
10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.
На этом все действия выполнены.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!
Порядок выполнения действий, правила, примеры
Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Порядок вычисления простых выражений
В случае выражений без скобок порядок действий определяется однозначно:
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Решение
17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
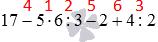
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Порядок вычислений в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:
Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Решение
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2
Начнем с умножения и деления, потом выполним вычитание и получим:
5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6
На этом вычисления можно закончить.
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Решение
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Решение
Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.
( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.