Что считать первым умножение или деление без скобок
Порядок выполнения действий, правила, примеры.
Числовые,буквенные выражения и выражения с переменными в своей записи могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий.
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок:
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: 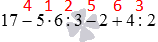
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени.
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции, то их значения вычисляются до выполнения остальных действий, при этом также учитываются правила из предыдущих пунктов, задающие порядок выполнения действий. Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.
Рассмотрим решения примеров.
Другие, в том числе и более сложные примеры выполнения действий в выражениях с корнями, степенями и т.п., Вы можете посмотреть в статье вычисление значений выражений.
интернет проект BeginnerSchool.ru
Сайт для детей и их родителей
Порядок выполнения математических действий
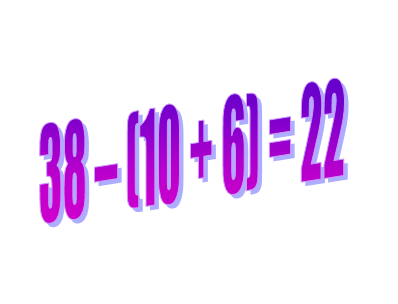
Порядок выполнения действий:
Читаем выражение слева направо и выбираем порядок действий по приоритету. Сначала выполняем действия в скобках. Затем умножение и/или деление. Далее складываем и вычитаем.
Если скобки имеют несколько вложений, то есть если внутри скобок есть ещё скобки, то сначала выполняем действия во внутренних скобках. Для простоты понимания, выражение в скобках можно воспринимать как самостоятельное выражение, то есть как отдельный пример, который надо решить. Внутри скобок действия выполняются согласно тому же порядку: Действия в скобках, затем умножение/деление, затем сложение/вычитание.
Умножение и деление не имеет между собой приоритета и выполняются слева направо, также как и сложение с вычитанием.
38 – (10 + 6) = 22;
Итак, вспомним о том, что сначала вычисляются выражения в скобках
1) в скобках: 10 + 6 = 16 ;
Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.
10 ÷ 2 × 4 = 20;
Порядок выполнения действий:
1) слева направо, сначала деление: 10 ÷ 2 = 5 ;
2) умножение: 5 × 4 = 20 ;
Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.
18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7
Порядок выполнения действий:
4) 9 – 6 = 3 ; т.е. слева направо – результат первого действия минус результат второго;
5) 3 + 4 = 7 ; т.е. результат четвертого действия плюс результат третьего;
Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.
1) выражение в скобках: 13 – 9 = 4 ;
2) умножение: 6 × 4 = 24 ;
3) сложение: 30 + 24 = 54 ;
Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:
1) действия, заключенные в скобках;
2) умножение и деление;
3) сложение и вычитание.
Если вы хотите получать анонсы наших статей подпишитесь на рассылку “Новости сайта“.
Оставляйте пожалуйста комментарии в форме ниже
Отзывов (60)
Полезная статья. Спасибо!
Очень все понятно. Для детей важна такая разъяснительная работа. Где Вы были, когда я пошла в школу?
)) Покажу сыну, пусть изучает. Я это вроде все помню. Спасибо )
Спасибо, сайт нужный. Честно говоря, уже кое – что подзабыла, а уроки с внучкой делаем. Вот, вспомнилось…
Очень необычная тематика сайта. Но тем, наверное, он и интересен. Иногда не знаешь, как объяснить ребенку тот или иной материал школьной программы.
Какое подспорье для родителей. И полезности для деток. Не всегда они материал усваивают в школе.
Сам учитель. Сайт очень полезный. Детям и родителям – хорошее подспорье
Помогите люди добрые.
Я тут читал кое где в иностранной литературе, что если в выражении есть действия двух уроовней 1(сложение и вычитание) и 2 (умножение и деление)
к примеру 20-6:3х2+2=
то в первую очередь должно выполнятся действия 2-ого уровня, потом 1-го. Но загвоздка с тем, что говорится – надо выполнить сперва умножение а потом деление, а не как нас учили по правилу слева направо.
Объясните плз.
Обязательно слева на право, так как умножение и деление равноценны. Но, если представить умножение в виде дроби:
тогда 2 перенесется в числитель и первым выполняется умножение
(6 * 2)/3 = (6:3)*2 = 4.
То есть порядок выполнения важен!
Помогите решить пример у всех расходятся ответы
6/2*(1+2)
ответь пожалуйста
Если 6 : 2 * (1 + 2) =
1) 1 + 2 = 3
2) 6 : 2 = 3
3) 3 * 3 = 9
Если
6
———-
2 * (1 + 2)
то есть 6 : (2 * (1 + 2))
1) 1 + 2 = 3
2) 2 * 3 = 6
3) 6 : 6 = 1
Это два разных примера.
Если
6 * (1 + 2)
———–
2
1) 1 + 2 = 3
2) 6 * 3 = 18
3) 18 : 2 = 9
Это тот же первый вариант
Если Вы правильно написали, то это первый вариант и ответ 9
Очень жаль, если вы этому детей учите.. Примеры 6:2*(1+2) и 6/2*(1+2) одинаковые… никогда не было такого, чтобы черта дроби и двоеточие означали разные действия или определяли порядок действий.
В данном случае необходимо также учесть правило раскрытия скобок:
6:2*(1+2) = 6:(2*1 + 2*2) = 6:(2+4) = 6:6 = 1 – единственный верный ответ.
6:2*(1+2) и 6/2*(1+2) это абсолютно эквивалентные записи (то есть одинаковые).
Порядок действий следующий:
1) 1+2 = 3
2) 6:2 = 3
3) 3*3 = 9
Ваш вариант с раскрытием скобок будет верен, если запись выражения будет следующей:
6:(2*(1+2)) = 1;
Ваше недоумение понятно, оно имеет глубокие исторические корни, в старых учебниках по алгебре можно встретить упоминание о именно такой последовательности действий, как предлагаете вы. Это связанно с неоднозначностью интерпретации записи. Но в наше время это разночтение устранено. Так что не надо забивать людям голову неверной информацией, а тем более забивать этими пережитками прошлого головы детей.
Простой пример. Ребенок на уроке информатики на языке Паскаль запишет y:=6:2*(1+2) и, поверьте мне, получит y=9. Не ломайте детскую психику.
В связи с порядком действий бывают забавные ситуации когда человеку в руки попадает калькулятор с обратной польской записью, а он и понятия не имеет об этом. И начинается “Святая Война за Истину”. Будьте проще, меньше пафоса, мы все люди и нам свойственно ошибаться. Добра Вам.
Урок 24 Бесплатно Порядок выполнения действий
Изучая числовые и буквенные выражения, способы упрощения выражений, свойства арифметических операций, мы рассматривали в основном простые выражения, значение которых найти было несложно.
Сегодня на уроке мы будем рассматривать выражения, в которых содержатся сразу несколько арифметических операций и несколько пар скобок.
Выясним, в какой последовательности необходимо выполнять математические операции при нахождении значения выражения.
Узнаем, какие действия называют действиями первой и второй ступени, зачем нужны скобки.
Разберем множество различных примеров, которые позволят нам лучше усвоить данную тему.
Порядок выполнения действий
Любой человек каждый день решает множество различных задач: простых и сложных.
Многие из них решаются по определенным правилам- алгоритмам.
У меня есть дополнительная информация к этой части урока!
Алгоритм- это определенная последовательность действий.
Алгоритм задает не только совокупность действий, но и порядок их выполнения.
Например, алгоритмом можно считать инструкцию по эксплуатации какого-либо прибора, рецепт приготовления блюда в кулинарной книге, порядок действий при включении компьютера, порядок выполнения практической работы, расписание уроков, режим дня, правила дорожного движения и многое другое.
Приведем пример простейшей последовательности действий (алгоритма) из повседневной жизни.
Порядок действий (алгоритм) открывания замка ключом.
Чтобы получить верный результат, необходимо соблюдать определенный порядок действий.
Если мы изменим порядок действий в рассмотренном алгоритме открывания замка ключом, то открыть его не получится.
На самом деле, не получится сначала вставить ключ в замочную скважину, а затем найти этот ключ, а если не вставить ключ в замочную скважину, то, конечно же, не удастся повернуть ключ и вытащить его.
С алгоритмами мы уже не раз встречались на наших уроках, решая задачи и уравнения, рассматривая различные правила и свойства, совершая вычисления в столбик и др.
Выясним зависит ли значение выражения от порядка выполнения арифметических операций, обязательно ли выполнять действия в определенном порядке.
Рассмотрим следующий пример:
Катя и Федя решали пример, в котором необходимо было найти сумму числа 24 и произведения чисел 8 и 2.
Катя записала пример: 24 + 8 ∙ 2 и принялась выполнять арифметические действия по порядку.
Первым делом она нашла сумму чисел 24 и 8.
Сложив 24 и 8, у нее получилось число 32.
24 + 8 = 32.
Затем полученный результат (число 32) она умножила на 2.
В итоге у нее получилось:
32 ∙ 2 = 64.
Ответ: 64.
Федя записал пример: 24 + 8 ∙ 2 и стал решать его иным способом.
Сначала он нашел произведение чисел 8 и 2.
Умножив 8 на 2, у него получилось число 16.
8 ∙ 2 = 16.
Затем к 24 прибавил полученное произведение.
В итоге получил следующее равенство:
16 + 24 = 40.
Ответ: 40.
Исходные выражения, которые записали Катя и Федя, были одинаковые (содержали определенную последовательность чисел и знаков).
Дети меняли только порядок следования математических операций.
В итоге получили различные значения одного и того же выражения.
Получается, что порядок выполнения арифметических действий влияет на результат вычислений.
Чуть позже мы выясним, кто же решил пример правильно: Катя или Федя.
Пройти тест и получить оценку можно после входа или регистрации
Порядок выполнения действий в выражениях без скобок
Очень часто в математических выражения присутствует сразу несколько арифметических операций, таких как сложение, вычитание, умножение и деление.
Чтобы найти значение такого выражения, необходимо соблюдать порядок действий, который регламентируется определенными правилами.
Рассмотрим правила выполнения арифметических действий в выражениях без скобок.
1. Математическое выражение вычисляется по частям, математические операции выполняются по порядку слева направо (от начала к концу выражения).
2. Арифметические действия делят на действия первой ступени и действия второй ступени.
Сложение и вычитание- это действия первой ступени.
Умножение и деление- это действия второй ступени.
3. Если в выражении без скобок присутствуют действия только первой ступени (сложение и вычитание), то действия выполняются в порядке их следования (слева направо).
У меня есть дополнительная информация к этой части урока!
Определим порядок действий в выражении и найдем его значение.
Данное выражение содержит действия только первой ступени (сложение и вычитание) и не содержит скобок, следовательно, необходимо выполнить действия по порядку их следования (слева направо).
Запись промежуточных вычислений (т.е. действий) можно оформить двумя способами.
Выполнив последнее действие, ответ записывают в исходный пример.
В нашем случае решение будет выглядеть так:
Для нашего примера решение будет выглядеть следующим образом:
4. Если в выражении без скобок присутствуют только действия второй ступени (умножение и деление), то данные действия выполняются в порядке их следования (слева направо).
Дано выражение 15 ∙ 6 ÷ 3 ∙ 10.
Определим порядок действий в выражении и найдем его значение.
Данное выражение не содержит скобки, и в нем присутствуют только действия второй ступени (умножение и деление), следовательно, действия выполнять необходимо слева направо по порядку их следования.
5. Если в выражении отсутствуют скобки, и оно содержит действия первой и второй ступени, то сначала выполняются действия второй ступени (умножение и деление) в порядке их следования слева направо, затем выполняются действия первой ступени (сложения и вычитания) так же в порядке их следования слева направо.
Данное выражение не содержит скобки, в нем присутствуют действия первой и второй ступени.
Следовательно, действия будем выполнять по порядку слева направо: сначала умножение и деление, а затем вычитание и сложение.
Вспомним пример, рассмотренный нами в начале урока, где Катя и Федя решали пример.
Решим этот пример сами, соблюдая порядок следования арифметических операций, и выясним, кто из ребят нашел правильный ответ.
Было дано выражение 24 + 8 ∙ 2.
В данном выражении присутствуют действия первой и второй ступени, соответственно, сначала мы должны выполнить умножение, затем полученный результат стожить.
Обозначим порядок действий в выражении и найдем его значение.
Пройти тест и получить оценку можно после входа или регистрации
Порядок выполнения действий в выражениях со скобками
В математике есть специальный символ, который указывает нужный порядок действий в выражении, этот символ называется скобки.
У меня есть дополнительная информация к этой части урока!
Скобки чаще всего используют как парный знак.
В паре первая скобка называется открывающей, вторая- закрывающей.
Скобки заключают некоторую часть целого математического выражения.
В математике существует несколько видов скобок, которые имеют свой конкретный смысл.
Наиболее распространенными являются три вида скобок: круглые скобки (…), квадратные скобки […] и фигурные скобки <…>.
В математике область применения скобок различна.
Скобки часто используют в выражениях для указания порядка выполнения арифметических действий.
В качестве такого указателя в основном используют парные круглые скобки
1. Запомните правило!
Действия, записанные в скобках, выполняются в первую очередь.
На примере рассмотрим использование скобок для указания порядка действий или изменении этого порядка.
Найдем значение этого выражения, используя правило, которое определяет порядок выполнения действий в математических выражениях.
Так как скобок в данном примере нет, то первым действием выполняется деление, затем- вычитание.
В результате получим следующее равенство:
Ответ: 4.
В итоге получим следующий результат:
Ответ: 12.
Мы можем заметить, что, изменив порядок действий с помощью скобок, изменилось значение выражения.
2. Если в скобках присутствуют действия первой и второй ступени, то в скобках сохраняется известный нам порядок действий: слева направо выполняются сначала действия деления и вычитания, затем по порядку слева направо сложение и вычитание.
Это выражение содержит скобки, поэтому выполним сначала действия в них.
Внутри скобок присутствуют действия первой и второй ступени.
Следовательно, выполним деление, затем сложение, находящееся в скобках.
Так как оставшиеся за скобками действия- это действия первой ступени, то они выполняются по порядку слева направо.
3. Существуют выражения, которые содержат несколько пар скобок, указывающих порядок выполнения действий.
В таком случае выполняются действия последовательно по порядку слева направо: сначала в первой паре скобок, затем во второй паре, далее в третьей и т.д. (пока есть скобки), и только потом выполняются все остальные действия, которые находятся за скобками, согласно правилам, определяющим порядок выполнения математических действий в выражениях.
Рассмотрим данное правило на примере.
Это выражение содержит скобки, поэтому выполним сначала действия в них.
Первым делом выполним все действия в первой скобке, причем сначала найдем произведение чисел, а затем сложение.
После этого выполняется действие во второй скобке.
Далее все остальные действия по уже известным нам правилам.
4. Иногда возникает ситуация, когда в выражении встречаются сложное сочетание скобок- вложенные скобки (будто скобки с выражениями вложены друг в друга).
У меня есть дополнительная информация к этой части урока!
Существует несколько вариантов, чтобы отличить одну пару скобок от другой:
1) Скобки обозначают разными размерами (обычно внутренние скобки изображают меньшего размера).
2) Изображают каждую пару скобок одним цветом, для каждой пары скобок один цвет.
3) Дополнительно применяют другие виды скобок.
Так, если выражение в круглых скобках нужно заключить в скобки, то для этого можно использовать квадратные скобки, а если необходимо в скобки заключить выражение, которое содержит круглые и квадратные скобки, то в таком случае можно использовать фигурные скобки
Последовательность действий для такого выражения определяется следующим правилом:
Если скобки содержат внутренние скобки, то сначала выполняются действия в них, затем математические операции проводят, продвигаясь последовательно ко внешним скобкам.
В качестве примера определим порядок действий в выражении
1) Первым делом выполним действие, которое находится в круглых скобках.
200 + 100 = 300
В исходное выражение вместо выражения, стоящего в круглых скобках, запишем найденное его значение.
Далее выполняем действия, находящиеся в квадратных скобках, соблюдая очередность действий первой и второй ступеней.
2) Найдем произведение 300 и 5.
300 ∙ 5 = 1500
3) Из полученного произведения вычтем 300.
Вместо выражения, которое находилось в квадратных скобках, запишем его значение.
Далее выполняем действия, находящиеся в фигурных скобках, соблюдая очередность действий первой и второй ступеней.
4) Найдем произведение 10 и 20.
10 ∙ 20 = 200
5) Полученный результат вычтем из 1200.
Подставим вместо выражения, стоящего в фигурных скобках, его значение.
В оставшейся части исходного выражения больше скобок нет, в нем присутствуют действия первой и второй ступени.
Следовательно, действия будем выполнять по порядку слева направо.
6) Сначала выполним деление:
1000 ÷ 20 = 50
7) Затем из полученного частного вычтем 10.
50 — 10 = 40
У меня есть дополнительная информация к этой части урока!
Порой, в выражениях скобки можно опустить, если при этом порядок действий не изменится.
Дано выражение (24 + 14) — 4.
Найдем значение этого выражения, используя правило, которое определяет порядок выполнения действий в математических выражениях.
Так как в данном примере есть скобки, то первым действием выполним сложение чисел 24 и 14, затем из полученной суммы вычтем число 4, стоящее за скобкой:
Получаем в результате ответ: число 34.
Рассмотрим другую ситуацию: выражение будет содержать все те же числа и математические операции, но будет записано без скобок 24 + 14 — 4.
Данное выражение содержит действия только первой ступени (сложение и вычитание) и не содержит скобок, следовательно, необходимо выполнять действия по порядку их следования слева направо.
Сначала выполним сложение, а затем вычитание:
Получаем в результате ответ: число 34.
Заметим, что порядок действий в выражении со скобками (24 + 14) — 4 и без скобок 24 + 14 — 4 одинаковый, и значения этих двух выражений равны.
Следовательно, для нашего случая верно равенство: (24 + 14) — 4 = 24 + 14 — 4
Порядок действий в выражениях можно изменять с помощью основных свойств сложения, вычитания, умножения и деления.
Например, дано выражение 7 ∙ 2 ∙ 55.
В данном выражении удобнее использовать сочетательное свойство умножения, а не выполнять действия по порядку.
Сначала найдем произведение 2 и 55, и только потом полученное произведение умножим на 7.
7 ∙ 2 ∙ 55 = 2 ∙ 55 ∙ 7 = 110 ∙ 7 = 770.
Свойства арифметических операций часто используют для упрощения выражений.
Важно отметить, что установленный порядок действий в выражениях без скобок и со скобками справедлив как для числовых выражений, так и для буквенных.
Представим в общем виде порядок выполнения арифметических действий в виде схемы.
У меня есть дополнительная информация к этой части урока!
Каждое выражение вычисляется по определенной программе (алгоритму), которую задают правила выполнения арифметических действий.
Записывая решение в виде равенств, оформляя каждое под своим номером в столбик, мы составляли алгоритм вычисления выражения такого вида:
1) 30 + 20 = 50
2) 800 ÷ 10 = 80
4) 50 ∙ 20 = 1000
Эту же программу вычислений можно представить в виде схемы, выполняя действия в определенном порядке, заполняя при этом последовательно пустые ячейки.
В нижней ячейке записывается ответ.
Пройти тест и получить оценку можно после входа или регистрации



























