Что считается углом между пересекающимися прямыми

Угол между пересекающимися прямыми – определение, примеры нахождения.

Начнем с краткого обзора материала статьи.

Сначала дано определение угла между пересекающимися прямыми с поясняющим рисунком. Далее показаны методы, позволяющие найти синус угла, косинус угла и сам угол между двумя пересекающимися прямыми на плоскости и в пространстве по известным уравнениям этих прямых в фиксированной прямоугольной системе координат, получены соответствующие формулы и приведены подробные решения примеров и задач.

Навигация по странице.

Чтобы определить угол между двумя пересекающимися прямыми нам потребуются определения, данные в статье геометрическая фигура угол и некоторые вспомогательные определения.

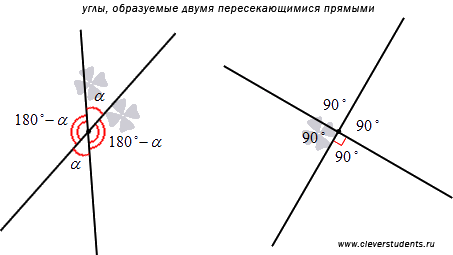
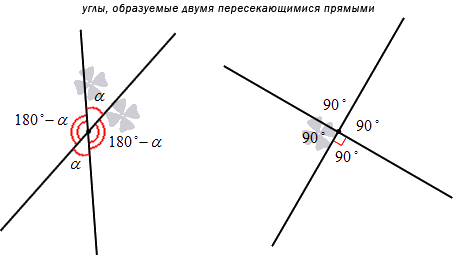
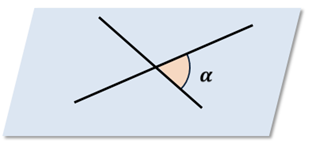
Две прямые называются пересекающимися, если они имеют одну единственную общую точку. Эта общая точка двух прямых называется точкой пересечения прямых. Точка пересечения разбивает каждую из пересекающихся прямых на два луча. Очевидно, эти лучи образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Таким образом, если нам известна мера одного из углов, образованных двумя пересекающимися прямыми, то мы можем определить меры трех остальных углов. Действительно, пусть один из углов равен углу . Тогда вертикальный с ним угол также равен , а смежные с ним углы равны . Если , то все четыре угла являются прямыми. В этом случае пересекающиеся прямые называются перпендикулярными (им посвящена статья перпендикулярные прямые).

Теперь можно переходить к определению угла между пересекающимися прямыми.

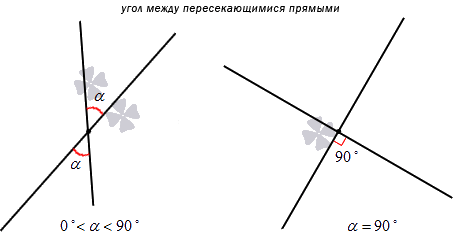
Угол между двумя пересекающимися прямыми – это мера меньшего из четырех углов, образованных этими прямыми.

Из приведенного определения следует, что градусная мера угла между двумя пересекающимися прямыми выражается действительным числом из интервала . Угол между перпендикулярными прямыми по определению равен девяноста градусам.

Нахождение угла между двумя пересекающимися прямыми на плоскости.

Существует множество разнообразных задач, в которых приходится находить угол между пересекающимися прямыми. В зависимости от условий этих задач подбирается подходящий метод решения.

Можно использовать методы геометрии. К примеру, если известны какие-либо дополнительные углы, то можно пробовать связать их с искомым углом между пересекающимися прямыми, отталкиваясь от равенства или подобия фигур. Если известны стороны треугольника и требуется найти угол между пересекающимися прямыми, на которых лежат стороны треугольника, то можно использовать теорему косинусов. При наличии прямоугольных треугольников отыскать угол между пересекающимися прямыми помогают определения синуса, косинуса и тангенса угла. Много подобных задач решается на уроках геометрии в средней школе.

Для нахождения углов между пересекающимися прямыми также прекрасно подходит метод координат. Давайте детально разберем его.

Решим поставленную задачу.

Мы знаем, что от прямой линии на плоскости в прямоугольной системе координат неотделим направляющий вектор прямой и нормальный вектор прямой, и мы можем по заданному уравнению прямой на плоскости определить координаты ее направляющего и нормального вектора. Таким образом, у нас есть возможность получить координаты направляющих и нормальных векторов заданных пересекающихся прямых.

Угол между заданными пересекающимися прямыми может быть найден через

Разберем каждый случай.

Разберем решение примера.

угол между указанными пересекающимися прямыми равен 45 градусам.

Основное тригонометрическое тождество позволяет найти синус угла при известном косинусе этого угла. Так как угол между двумя пересекающимися прямыми не тупой, то .

Тогда .

Осталось разобраться, как найти угол между пересекающимися прямыми, если известен направляющий вектор одной прямой и нормальный вектор другой прямой.

Если угол между векторами и не превосходит 90 градусов, то он дополняет угол между пересекающимися прямыми a и b до прямого угла, то есть, , если . Если же , то .
Так как косинусы равных углов равны, то последние равенства можно записать в виде , если , и , если . Следовательно,

(Обратите внимание: заданные прямые совпадают с прямыми из предыдущего примера).

Очевидно, получили такой же угол между пересекающимися прямыми, как и в предыдущем примере.

Дадим еще формулу для нахождения угла между двумя пересекающимися прямыми a и b через угловые коэффициенты этих прямых.

Определите угол между пересекающимися прямыми и .

(В условии даны все те же пересекающиеся прямые из предыдущих примеров).

Заданные прямые имеют угловые коэффициенты и . Подставляем эти значения в формулу для нахождения угла между пересекающимися прямыми по угловым коэффициентам:

В заключении этого пункта отметим, что совсем не обязательно запоминать все выведенные формулы для нахождения угла между пересекающимися прямыми на плоскости. Достаточно понимать, что угол между пересекающимися прямыми может быть найден с помощью угла между направляющими или нормальными векторами прямых, уметь определять координаты этих векторов по известным уравнениям прямых, а также помнить формулу для вычисления косинуса угла между двумя векторами.

Нахождение угла между двумя пересекающимися прямыми в пространстве.

Нахождение угла между двумя пересекающимися прямыми в пространстве методом координат сводится к нахождению координат направляющих векторов этих прямых и последующему определению угла между ними. При этом все рассуждения из предыдущего пункта, касающиеся определения угла между пересекающимися прямыми через угол между их направляющими векторами, остаются справедливыми.

Пусть искомый угол между пересекающимися прямыми равен . Направляющим вектором прямой является вектор , а в качестве направляющего вектора оси аппликат можно принять координатный вектор . Теперь у нас есть все данные, чтобы применить формулу для нахождения косинуса угла между пересекающимися прямыми:

Тогда искомый угол между пересекающимися прямыми равен .

Источник

Угол между прямыми

Определение угла между прямыми

Угол между прямыми на плоскости

Угол между прямыми заданными уравнениями с угловым коэффициентом

то угол между ними можно найти, используя формулу:

Если знаменатель равен нулю (1 + k ₁· k ₂ = 0), то прямые перпендикулярны.

Соответственно легко найти угол между прямыми

Угол между прямыми через направляющие векторы этих прямых

cos φ = | a · b | | a | · | b |

Если уравнение прямой задано параметрически

x = l t + a y = m t + b

то вектор направляющей имеет вид

Если уравнение прямой задано как

Если дано каноническое уравнение прямой

то вектор направляющей имеет вид

Если задано уравнение прямой с угловым коэффициентом

то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b ), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b ). Вектор направляющей KM =

Угол между прямыми через векторы нормалей этих прямых

cos φ = | a · b | | a | · | b |

Если уравнение прямой задано как

то вектор нормали имеет вид

Если задано уравнение прямой с угловым коэффициентом

то вектор нормали имеет вид

Угол между прямыми через направляющий вектор и вектор нормали этих прямых

sin φ = | a · b | | a | · | b |

Примеры задач на вычисления угла между прямыми на плоскости

Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:

Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.

Для первой прямой направляющий вектор <1; 2>, для второй прямой направляющий вектор

cos φ = |1 · 2 + 2 · 1| 1 2 + 2 2 · 2 2 + 1 2 = 4 5 · 5 = 0.8

Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.

Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.

Угол между прямыми в пространстве

cos φ = | a · b | | a | · | b |

Если дано каноническое уравнение прямой

то направляющий вектор имеет вид

Если уравнение прямой задано параметрически

x = l t + a y = m t + b z = n t + c

то направляющий вектор имеет вид

cos φ = |2 · 1 + 1 · (-2) + (-1) · 0| 2 2 + 1 2 + (-1) 2 · 1 2 + (-2) 2 + 0 2 = 0 6 · 5 = 0

Решение: Для решения этой задачи найдем направляющие векторы этих прямых.

Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор <3; 4; 5>.

Преобразуем второе уравнение к каноническому вид.

Получено уравнение второй прямой в канонической форме

Источник

Угол между пересекающимися прямыми: определение, примеры нахождения

Данный материал посвящен такому понятию, как угол между двумя пересекающимися прямыми. В первом пункте мы поясним, что он из себя представляет, и покажем его на иллюстрациях. Потом разберем, какими способами можно найти синус, косинус этого угла и сам угол (отдельно рассмотрим случаи с плоскостью и трехмерным пространством), приведем нужные формулы и покажем на примерах, как именно они применяются на практике.

Что такое угол между пересекающимися прямыми

Для того чтобы понять, что такое угол, образующийся при пересечении двух прямых, нам потребуется вспомнить само определение угла, перпендикулярности и точки пересечения.

Мы называем две прямые пересекающимися, если у них есть одна общая точка. Эта точка называется точкой пересечения двух прямых.

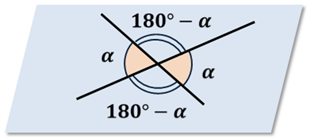
Каждая прямая разделяется точкой пересечения на лучи. Обе прямые при этом образуют 4 угла, из которых два – вертикальные, а два – смежные. Если мы знаем меру одного из них, то можем определить и другие оставшиеся.

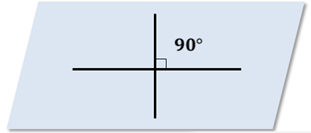
Взгляните на рисунок:

Перейдем к формулированию основного определения.

Как найти угол между пересекающимися прямыми на плоскости

Умение находить меру угла между двумя пересекающимися прямыми полезно для решения многих практических задач. Метод решения можно выбрать из нескольких вариантов.

Для начала мы можем взять геометрические методы. Если нам известно что-то о дополнительных углах, то можно связать их с нужным нам углом, используя свойства равных или подобных фигур. Например, если мы знаем стороны треугольника и нужно вычислить угол между прямыми, на которых эти стороны расположены, то для решения нам подойдет теорема косинусов. Если у нас в условии есть прямоугольный треугольник, то для подсчетов нам также пригодится знание синуса, косинуса и тангенса угла.

Координатный метод тоже весьма удобен для решения задач такого типа. Поясним, как правильно его использовать.

Начнем с формулировки основного принципа нахождения угла в заданных условиях.

Нам известно, что с понятием прямой линии тесно связаны такие понятия, как направляющий и нормальный вектор. Если у нас есть уравнение некоторой прямой, из него можно взять координаты этих векторов. Мы можем сделать это сразу для двух пересекающихся прямых.

Угол, образуемый двумя пересекающимися прямыми, можно найти с помощью:

Теперь рассмотрим каждый способ отдельно.

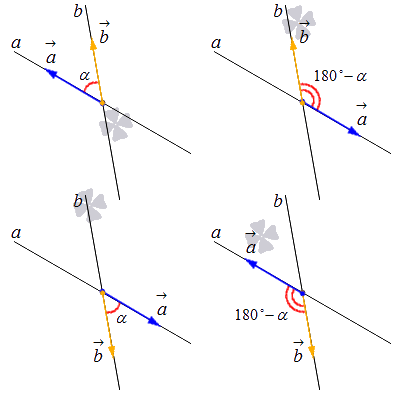
Во втором случае были использованы формулы приведения. Таким образом,

Запишем последнюю формулу словами:

Косинус угла, образованного двумя пересекающимися прямыми, будет равен модулю косинуса угла между его направляющими векторами.

Из нее мы можем вывести формулу косинуса угла между двумя заданными прямыми:

cos α = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2 = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2

Тогда сам угол можно найти по следующей формуле:

α = a r c cos a x · b x + a y + b y a x 2 + a y 2 · b x 2 + b y 2

Приведем пример решения задачи.

Решение

Ответ: данные прямые образуют угол в 45 градусов.

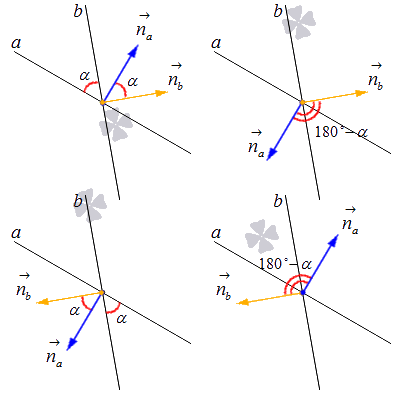
Формулы для вычисления косинуса угла между пересекающимися прямыми и самого этого угла с помощью координат нормальных векторов выглядят так:

Здесь n a → и n b → обозначают нормальные векторы двух заданных прямых.

Решение

Разберем последний случай – нахождение угла между прямыми, если нам известны координаты направляющего вектора одной прямой и нормального вектора другой.

Если величина угла между заданными векторами не более 90 градусов, получается, что он будет дополнять угол между a и b до прямого угла.

Если он менее 90 градусов, то мы получим следующее:

Используя правило равенства косинусов равных углов, запишем:

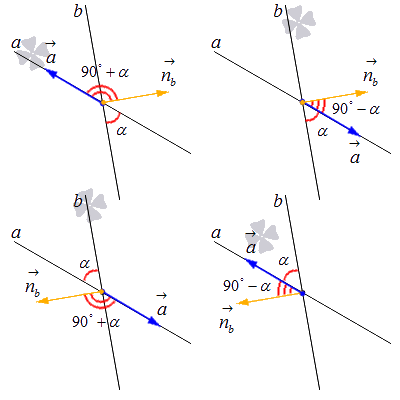
Чтобы найти синус угла между двумя прямыми, пересекающимися на плоскости, нужно вычислить модуль косинуса угла между направляющим вектором первой прямой и нормальным вектором второй.

Запишем необходимые формулы. Нахождение синуса угла:

Нахождение самого угла:

α = a r c sin = a x · n b x + a y · n b y a x 2 + a y 2 · n b x 2 + n b y 2

Здесь a → является направляющим вектором первой прямой, а n b → – нормальным вектором второй.

Решение

Обратите внимание, что мы взяли уравнения из предыдущей задачи и получили точно такой же результат, но другим способом.

Ответ: α = a r c sin 7 2 34

Приведем еще один способ нахождения нужного угла с помощью угловых коэффициентов заданных прямых.

Решение

Ответ: α = a r c cos 23 2 34

В выводах этого пункта следует отметить, что приведенные здесь формулы нахождения угла не обязательно учить наизусть. Для этого достаточно знать координаты направляющих и/или нормальных векторов заданных прямых и уметь определять их по разным типам уравнений. А вот формулы для вычисления косинуса угла лучше запомнить или записать.

Как вычислить угол между пересекающимися прямыми в пространстве

Вычисление такого угла можно свести к вычислению координат направляющих векторов и определению величины угла, образованного этими векторами. Для таких примеров используются такие же рассуждения, которые мы приводили до этого.

Для нахождения самого угла нам понадобится эта формула:

α = a r c cos a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2

Решение

Источник

Угол между прямыми

Урок 9. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Угол между прямыми»

· рассмотрим углы между пересекающимися и скрещивающимися прямыми в пространстве.

Напомню, что два луча ОА и O₁A₁ в пространстве, не лежащие на одной прямой, называются сонаправленными, если они параллельны и лежат в одной полуплоскости с границей ОO₁. Если стороны двух углов соответственно сонаправленны, то такие углы равны.

Как вы уже знаете, любые две пересекающиеся прямые лежат в одной плоскости и образуют четыре неразвернутых угла. Если известен один из этих углов, то можно найти и другие три угла.

Определение. Если пересекающиеся прямые образуют тупые и острые углы, то углом между этими прямыми называется тот, который не превосходит любой из трех остальных углов, т.е. наименьший из углов.

Если пересекающиеся прямые образуют четыре равных угла, то угол между этими прямыми равен девяносто градусов.

Пусть α – тот из углов, который не превосходит любого из трех остальных углов. Тогда говорят, что угол между пересекающимися прямыми равен α. Очевидно, что угол альфа между двумя пересекающимися прямыми удовлетворяет условию: .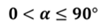

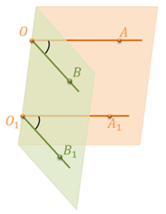
Теперь введем понятие угла между скрещивающимися прямыми. Пусть нам даны две скрещивающиеся прямые а и b. Возьмем произвольную точку М₁ в пространстве и проведем через нее прямые A₁B₁, параллельные прямым а и b соответственно.

Тогда углом между скрещивающимися прямыми а и b называется угол между построенными пересекающимися прямыми A₁B₁. Т. е. если угол между прямыми A₁B₁ равен φ, то будем говорить, что угол между скрещивающимися прямыми а и b равен φ.

Докажем, что угол между скрещивающимися прямыми не зависит от выбора точки М₁.

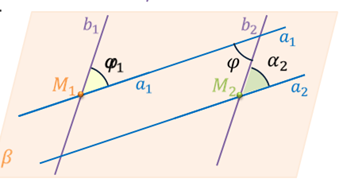
Возьмем любую другую точку М₂ и проведем через нее прямые a₂ и b₂, параллельные прямым а и b соответственно. Пусть угол между прямыми a₁ и b₁ равен α₁, а угол между прямыми a₂ и b₂ равен α₂.

Если прямые a₁, b₁, a₂, b₂ лежат в одной плоскости, то по свойству накрест лежащих углов при параллельных прямых угол α₁ равен углу φ и равен углу α₂.

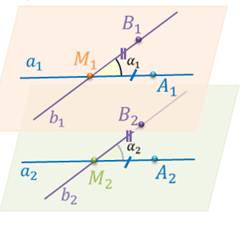
Пусть теперь прямые a₁ и b₁, пересекающиеся в точке М₁, лежат в одной плоскости. А прямые a₂ и b₂, пересекающиеся в точке М₂ лежат в другой плоскости.

Так как прямая a₁ параллельна прямой а и прямая a₂ параллельна прямой а, то по признаку параллельности прямых в пространстве прямые a₁ и a₂ также параллельны. Так как прямая b₁ параллельна прямой b и прямая b₂ параллельна прямой b, то по признаку параллельности прямых в пространстве прямые b₁ и b₂ параллельны.

Отметим на прямых a₁ и a₂ точки A₁ и A₂ так, чтобы отрезки М₁А₁ и М₂А₂ были равны. На прямых b₁ и b₂ отметим точки B₁ и B₂ так, чтобы отрезки M₁B₁и M₂B₂ были равны.

Тогда стороны угла A₁M₁B₁ и угла A₂M₂B₂ попарно сонаправлены. По теореме о равенстве углов с сонаправленными сторонами получаем, что угол A₁M₁B₁ равен углу A₂M₂B₂. Т. е. имеем, что угол α₁ равен углу α₂.

Таким образом, величина угла между скрещивающимися прямыми не зависит от выбора точки M₁.

Замечание. Угол между параллельными прямыми в пространстве считается равным 0º.

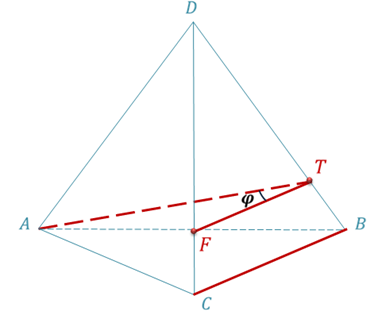
Рассмотрим пример. Пусть у нас есть треугольная пирамида DABC. На ее ребре DB взята точка Т.

Тогда угол между скрещивающимися прямыми BC и АТ равен углу между прямой АТ и прямой TF, которая проходит через точку Т параллельно прямой BC в плоскости BDC.

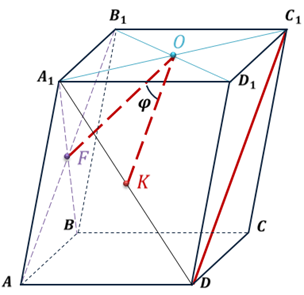
Рассмотрим еще пример. Пусть есть параллелепипед ABCDA₁B₁C₁D₁. И пусть точка О – точка пересечения диагоналей грани A₁B₁C₁D₁, а точка F – точка пересечения диагоналей грани AA₁B₁B.

Тогда угол между скрещивающимися прямыми C₁D и OF равен углу между прямыми OF и прямой OK, проходящей через точку О и параллельной прямой C₁D в плоскости C₁DA₁.

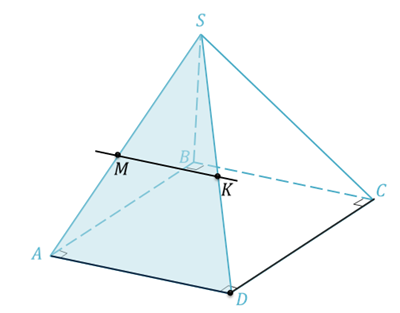
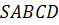
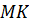
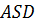
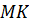
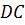
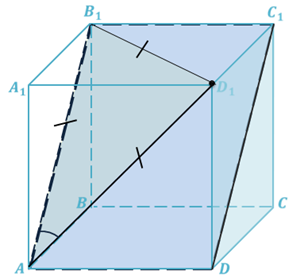
Задача. Дана правильная пирамида . – средняя линия грани . Найдите угол между прямыми и .

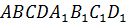
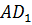
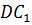
Задача. Дан куб . Найдите угол между прямыми и .

Подведем итоги урока. На этом уроке мы рассмотрели углы между пересекающимися и скрещивающимися прямыми. А также решили несколько задач на нахождение скрещивающихся углов.

Источник