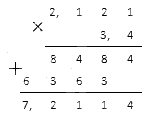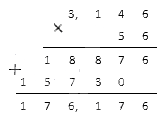Что считается суммой двух положительных рациональных чисел
Положительные рациональные числа
Отношение равенства является отношением эквивалентности на множестве дробей, поэтому оно порождает на нем классы эквивалентности. В каждом таком классе содержатся равные между собой дроби. Например, множество дробей 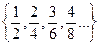
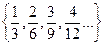
Определение. Положительным рациональным числом называется класс равных дробей, а каждая дробь, принадлежащая этому классу, есть запись (представление) этого числа.
Например, о дроби 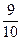
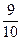
Множество всех положительных рациональных чисел принято обозначать символом Q+. Определим на этом множестве отношение равенства.
Из данного определения следует, что равные рациональные числа представляются равными дробями. Среди всех записей любого положительного рационального числа выделяют дробь, которая является несократимой, и доказывают, что любое рациональное число представимо единственным образом несократимой дробью (мы это доказательство опускаем).
Для того чтобы рациональное число 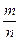
Выясним теперь, как определяются арифметические действия с положительными рациональными числами.
Таким образом, по определению, 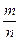

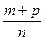
Можно доказать, что при замене дробей 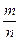

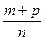
В определении суммы рациональных чисел мы использовали их представления в виде дробей с одинаковыми знаменателями. Если же числа а и b представлены дробями с различными знаменателями, то сначала надо привести их к одному знаменателю, а затем применять правило (1).
Сложение положительных рациональных чисел коммутативно и ассоциативно,
( 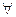
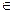
( 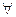
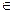
Прежде чем сформулировать определение умножения положительных рациональных чисел, рассмотрим следующую задачу: известно, что длина отрезка X выражается дробью 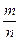
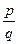
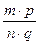
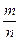
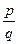
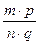
Таким образом, по определению, 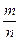
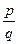
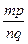
Можно доказать, что при замене дробей 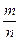
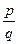
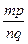
Умножение положительных рациональных чисел коммутативно, ассоциативно и дистрибутивно относительно сложения и вычитания. Доказательство этих свойств основывается на определении умножения и сложения положительных рациональных чисел, а также на соответствующих свойствах сложения и умножения натуральных чисел.
Определение сложения положительных рациональных чисел дает возможность определить отношение «меньше» на множестве Q+.
В этом же случае считают, что число а больше числа b. Пишут b b.
Так определенное отношение «меньше» обладает рядом свойств, которые мы приводим без доказательства.
1. Отношение «меньше» на множестве Q+ антисимметрично и транзитивно, т.е. является отношением порядка, а множество Q+ упорядоченным множеством.
2. Если рациональные числа а и b представлены дробями 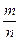
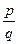
Дата добавления: 2017-06-02 ; просмотров: 2293 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Положительные рациональные числа
Отношение равенства является отношением эквивалентности на множестве дробей, поэтому оно порождает на нём классы эквивалентности. В каждом таком классе содержатся равное между собой дроби. Например, множество дробей <







Дроби одного класса выражают длину одного и того же отрезка. Но длина отрезка должна представляться единственным числом. Поэтому считают, что равные дроби – это различные записи одного и того же положительного рационального числа.
Положительным рациональным числом называется класс дробей, а каждая дробь, принадлежащая этому классу, есть запись (представление) этого числа.
Например, о дроби 

Множество всех положительных рациональных чисел принято обозначать символом Q+. Определим на это множество отношение равенства.
Если положительное рациональное число a представить дробью 

Из данного определения следует, что равные рациональные числа представляются равными дробями. Среди всех записей любого положительного рационального числа выделяют дробь, которая является несократимой, и доказывают, что любое рациональное число представимо единственным образом несократимой дробью (мы это доказательство опускаем). Для того чтобы рациональное число 
Выяснить теперь, как определяются арифметические действия с положительными рациональными числами.
Пусть при некотором единственном отрезке e длина отрезка x выражается дробью 



Если положительное рациональное число a представить дробью 


Таким образом по определению

Можно доказать, что при замене дробей 


В определении суммы рациональных чисел мы использовали их представления в виде дробей с одинаковыми знаменателями. Если же числа а и b представлены дробями с различными знаменателями, то сначала надо привести их к одному знаменателю, а затем применить правило (1).
Сложение положительных рациональных чисел коммутативно и ассоциативно,
( 
( 
Докажем, например, коммутативность сложения. Представим числа а и b дробями 



Если положительное числа а представлено дробью 


Таким образом, по определению,

Умножение положительных рациональных чисел коммутативно, ассоциативно и дистрибутивно относительно сложения и вычитания. Доказательство этих свойств основывается на определении умножения и сложения положительных рациональных чисел, а также на соответствующих свойствах сложения и умножения натуральных чисел.
Определение сложения положительных рациональных чисел дает возможность определить отношение «меньше» на множестве Q+.
Пусть a и b — положительные рациональные числа. Считают, что число b меньше числа а, если существует такое положительное рациональное число с, что а =b + с.
В этом же случае считают, что число а больше числа b. Пишут b b.
Так определенное отношение «меньше» обладает рядом свойств, которые мы приводим без доказательства.
1. Отношение «меньше» на множестве Q+ антисимметрично и транзитивно, т.е. является отношением порядка, а множество Q+ упорядоченным множеством.
2. Если рациональные числа a и b представлены дробями 

Действия с рациональными числами: правила, примеры, решения
Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.
Действие сложения рациональных чисел
Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5 + 1 4 возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.
Сформулируем правила сложения рациональных чисел:
Сложение нуля с отличным от него рациональным числом
Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a .
Сложение противоположных рациональных чисел
Сумма противоположных чисел равна нулю.
Сложение положительных рациональных чисел
В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.
Решение
Осуществим сложение дробей с разными знаменателями:
6 10 + 5 9 = 54 90 + 50 90 = 104 90 = 1 7 45
Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.
Сложение рациональных чисел с разными знаками
Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.
Решение
Сложение отрицательных рациональных чисел
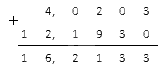
Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.
Решение
Действие вычитания рациональных чисел
При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.
Решение
Необходимо из рационального числа 2 7 вычесть рациональное число 5 3 7
Решение
Действие умножения рациональных чисел
Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.
Умножение на нуль
Произведение любого рационального числа a на нуль есть нуль.
Умножение на единицу
Т.е. a · 1 = a или 1 · a = a (для любого рационального a ). Единица здесь является нейтральным числом по умножению.
Умножение взаимообратных чисел
К примеру, результатом произведения чисел 5 6 и 6 5 будет единица.
Умножение положительных рациональных чисел
В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.
Решение
Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.
Решение
Перемножим десятичные дроби столбиком:
В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.
Умножение рациональных чисел с разными знаками
Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.
Решение
Умножение отрицательных рациональных чисел
Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.
Перемножим их столбиком:
Полученный результат и будет являться искомым произведением.
Деление рациональных чисел
На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.
Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.
Решение
Сложение рациональных чисел, правила и примеры.
Сложение рациональных чисел происходит по правилам сложения дробей. В этой теме рассмотрим подробно как складывать положительные и отрицательные рациональные числа, а также рациональные числа с одинаковыми и разными знаменателями.
Тема. Сложение рациональных чисел с одинаковыми знаменателями.
Определение:
Сумма дробей с одинаковыми положительными знаменателями, есть дробь с тем же знаменателем и суммой их числителей.
Правила сложения рациональных чисел.
Пример:
Выполните сложение рациональных чисел с одинаковыми знаменателями: а) \(\frac<-3><4>+\frac<1><4>\) б) \(\frac<-6><13>+\frac<-2><13>\) в) \(\frac<17><47>+\frac<12><47>\) г) \(\frac<32><15>+\frac<-12><15>\)
Решение:
а) Так как знаменатели у дробей одинаковые, записываем знаменатель тот же. Числители складываем по правилу сложения целых чисел. Итоговую дробь \(\frac<-2><4>\) сокращаем на 2.
Урок. Сложение рациональных чисел с разными знаменателями.
Определение:
Чтобы сложить две дроби с разными знаменателями необходимо сначала найти общий знаменатель, а потом сложить их числители.
Формула сложение рациональных чисел с разными знаменателями:
Алгоритм действия при сложении рациональных чисел с разными знаменателями.
Пример:
Выполните сложение рациональных чисел с разными знаменателями: а) \(\frac<-4><7>+\frac<5><8>\) б) \(\frac<-3><11>+\frac<-7><22>\) в) \(\frac<11><15>+\frac<9><25>\) г) \(\frac<8><3>+\frac<-1><13>\)
Решение:
а) Дроби \(\frac<-4><7>+\frac<5><8>\) имеют разные знаменатели, поэтому нужно найти общий знаменатель. Общий знаменатель будет равен 56, поэтому первую дробь \(\frac<-4><7>\) умножаем на 8, а вторую дробь \(\frac<5><8>\) на 7
б) Так как у дробей разные знаменатели, находим общий знаменатель. Общий знаменатель равен 22.
в) У дробей \(\frac<11><15>\) и \(\frac<9><25>\) разные знаменатели. Находим общий знаменатель, он равен 75. Первую дробь умножаем на 5, а вторую дробь умножаем на 3.
г) Общий знаменатель этих дробей \(\frac<8><3>\) и \(\frac<-1><13>\) равен 39.
Сложение противоположных рациональных чисел.
Правило сложения противоположных рациональных чисел.
Результатом сложения противоположных рациональных чисел будет нуль.
Сложение положительных рациональных чисел.
Сложение положительных рациональных чисел сводится к сложение обыкновенных дробей. Может быть два варианта:
Примеры:
Выполните сложение положительных рациональных дробей: а) \(\frac<4><15>+\frac<7><15>\) б) \(\frac<3><8>+\frac<5><12>\).
б) У дробей разные знаменатели нужно найти общий знаменатель. Общий знаменатель равен 24.
Сложение отрицательных рациональных чисел.
Складываем отрицательные рациональные числа по этим правилам:
Пример:
Сложите отрицательные рациональные числа: а) \(-\frac<13><19>+(-\frac<1><19>)\) б) \(-\frac<1><49>+(-\frac<5><14>)\).
б) Для начала найдем общий знаменатель. Общий знаменатель у дробей равен 98.
Сложение рациональных чисел с разными знаками, примеры.
Пример:
Выполните сложение рациональных чисел с разными знаками: а) \(-\frac<2><5>+\frac<1><5>\) б) \(\frac<1><27>+(-\frac<5><9>)\)
Решение:
а) У дробей общий знаменатель, переходим к сложению числителей. Определим какой знак будет в результате. Для этого посмотри модуль какого числа больше |-2|=2 и |1|=1. Получаем 2>1, то есть модуль отрицательного числа больше модуля положительного, поэтому в ответе будет стоять знак минус. Если сказать проще, у нас два минуса и один плюс. Минусов больше поэтому в результате поставим знак минус.
б) Сначала приведем к общему знаменателю, он равен 27, а потом сложим числители. Определим знак ответа. Найдем модули чисел |-15|=15 и |1|=1. Модуль отрицательного числа больше положительного 15>1, поэтому в ответе будет знак минус.