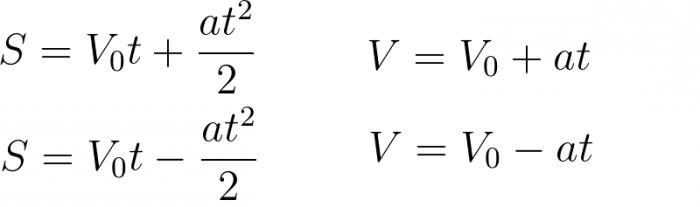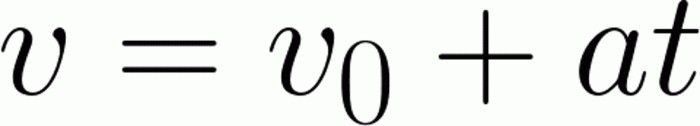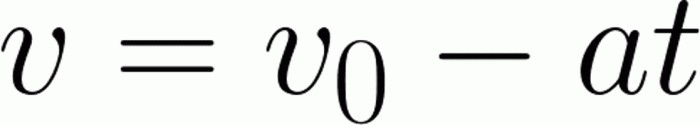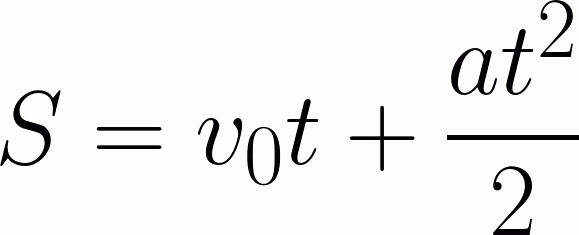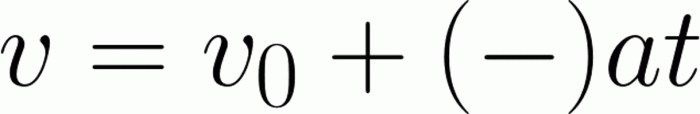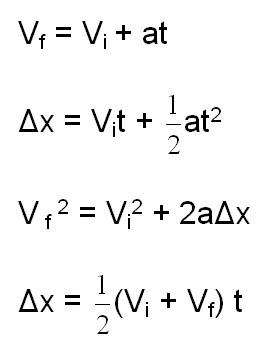Что считается материальной точкой
Материальная точка
Для описания движения тела нужно знать, как движутся различные его точки. Однако в случае поступательного движения все точки тела движутся одинаково. Поэтому для описания поступательного движения тела достаточно описать движение одной его точки.
Также во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно описывать как точку.
Слово «материальная» подчеркивает здесь отличие этой точки от геометрической. Геометрическая точка не обладает никакими физическими свойствами. Материальная точка может обладать массой, электрическим зарядом и другими физическими характеристиками.
Одно и то же тело в одних условиях можно считать материальной точкой, а в других – нет. Так, например, рассматривая движение корабля из одного морского порта в другой, корабль можно считать материальной точкой. Однако, при исследовании движения шарика, который катится по палубе корабля, корабль считать материальной точкой нельзя. Движение зайца, убегающего по лесу от волка, можно описывать, приняв зайца за материальную точку. Но нельзя считать зайца материальной точкой, описывая его попытки спрятаться в нору. При изучении движения планет вокруг Солнца их можно описывать материальными точками, а при суточном вращении планет вокруг своей оси такая модель неприменима.
Важно понимать, что в природе материальных точек не существует. Материальная точка – это абстракция, модель для описания движения.
Примеры решения задач по теме «Материальная точка»
| Задание | Можно ли принять за материальную точку: а) автомобиль, въезжающий в гараж; б) автомобиль на трассе Москва-Ярославль? |
| Ответ | а) автомобиль, въезжающий в гараж нельзя принять за материальную точку, так как в данных условиях существенны размеры автомобиля; |
б) автомобиль на трассе Москва-Ярославль можно принять за материальную точку, так как размеры автомобиля намного меньше расстояния между городами.
| Задание | Указать, в каких из приведенных ниже случаях изучаемое тело можно принять за материальную точку: а) рассчитывают давление трактора на грунт; б) вычисляют высоту, на которую поднялась ракета; в) рассчитывают работу при поднятии в горизонтальном положении плиты перекрытия известной массы на заданную высоту; г) определяют объем стального шарика при помощи измерительного цилиндра (мензурки). |
| Ответ | а) при расчете давления трактора на грунт трактор нельзя принять за материальную точку, так как в данном случае важно знать площадь поверхности гусениц; |
б) при расчете высоты подъема ракеты, ракету можно считать материальной точкой, так как ракета движется поступательно и расстояние, пройденное ракетой. намного больше ее размеров;
в) в данном случае плиту перекрытия можно считать материальной точкой. так как она совершает поступательное движение и для решения задачи достаточно знать перемещение ее центра масс;
г) при определении объема шарика. шарик считать материальной точкой нельзя, потому что в данной задаче существенны размеры шарика.
| Задание | Можно ли принять Землю за материальную точку при расчете: а) расстояния от Земли до Солнца; б) пути, пройденного Землей по орбите вокруг Солнца; в) длины экватора Земли; г) скорости движения точки экватора при суточном вращении Земли вокруг оси; д) скорости движения Земли по орбите вокруг Солнца? |
| Ответ | а) в данных условиях Землю можно принять за материальную точку, так как ее размеры намного меньше расстояния от нее до Солнца; |
б) в данных условиях Землю можно считать материальной точкой, так как путь, который она проходит по орбите намного превышает ее размеры;
в) при измерении длины экватора Землю считать материальной точкой нельзя, потому что в данном случае имеют значения размеры Земли;
г) в данном случае Землю нельзя считать материальной точкой, так при измерении скорости движения точки экватора при суточном вращении планеты, важны размеры планеты и ее форма;
д) в данном случае Землю можно принять за материальную точку, так как размеры орбиты намного превосходят размеры Земли.
МАТЕРИАЛЬНАЯ ТОЧКА
МАТЕРИАЛЬНАЯ ТОЧКА, вводимое в механике понятие об объекте исчезающе малых размеров, имеющем массу. Положение М. т. в пространстве определяется как положение геометрич. точки, что существенно упрощает решение задач механики. Практически данное тело можно рассматривать как М. т. в случаях, когда оно движется поступательно или когда расстояния, проходимые точками тела, очень велики по сравнению с его размерами. При движении любой меха-нич. системы (в частности, твёрдого тела) её центр масс (центр тяжести) движется так же, как двигалась бы М. т. с массой, равной массе всей системы, под действием всех внешних сил, приложенных к системе.
Смотреть что такое МАТЕРИАЛЬНАЯ ТОЧКА в других словарях:
МАТЕРИАЛЬНАЯ ТОЧКА
масса, которую мы воображаем сосредоточенной в одной геометрической подвижной точке. Назначение материальной точки в механике состоит в том, чтобы заме. смотреть
МАТЕРИАЛЬНАЯ ТОЧКА
вводимое в механике понятие об объекте исчезающе малых размеров, имеющем массу. Положение М. т. в пространстве определяется как положение геоме. смотреть
МАТЕРИАЛЬНАЯ ТОЧКА
Материальная точка — масса, которую мы воображаем сосредоточенной в одной геометрической подвижной точке. Назначение материальной точки в механике состоит в том, чтобы заменять собой такие тела, размерами которых мы пренебрегаем сравнительно с длинами, рассматриваемыми в данном вопросе. Напр. в тех вопросах астрономии, в которых не принимаются в расчет вращательные движения светил около их осей, каждое светило заменяется точкой, масса которой равна массе светила.
МАТЕРИАЛЬНАЯ ТОЧКА
МАТЕРИАЛЬНАЯ ТОЧКА
МАТЕРИАЛЬНАЯ ТОЧКА
МАТЕРИАЛЬНАЯ ТОЧКА
МАТЕРИАЛЬНАЯ ТОЧКА
МАТЕРИАЛЬНАЯ ТОЧКАВ механике: бесконечно малое тело.Словарь иностранных слов, вошедших в состав русского языка.- Чудинов А.Н.,1910.
МАТЕРИАЛЬНАЯ ТОЧКА
МАТЕРИАЛЬНАЯ ТОЧКА, точка, имеющая массу. В механике понятием материальная точка пользуются в случаях, когда размеры и форма тела при изучении его движения не играют роли, а важна только масса. Практически любое тело можно рассматривать как материальную точку, если оно движется поступательно и расстояния, проходимые им, велики по сравнению с его размерами.
МАТЕРИАЛЬНАЯ ТОЧКА
МАТЕРИАЛЬНАЯ ТОЧКА
МАТЕРИАЛЬНАЯ ТОЧКА
МАТЕРИАЛЬНАЯ ТОЧКА, точка, имеющая массу. В механике понятием материальная точка пользуются в случаях, когда размеры и форма тела при изучении его движения не играют роли, а важна только масса. Практически любое тело можно рассматривать как материальную точку, если оно движется поступательно и расстояния, проходимые им, велики по сравнению с его размерами. смотреть
МАТЕРИАЛЬНАЯ ТОЧКА
понятие, вводимое в механике для объекта бесконечно малых размеров, имеющего массу. Положение М. т. в пространстве определяется как положение геом. точ. смотреть
МАТЕРИАЛЬНАЯ ТОЧКА
— точка, имеющая массу. В механике понятиемматериальная точка пользуются в случаях, когда размеры и форма тела приизучении его движения не играют роли, а важна только масса. Практическилюбое тело можно рассматривать как материальную точку, если оно движетсяпоступательно и расстояния, проходимые им, велики по сравнению с егоразмерами. смотреть
МАТЕРИАЛЬНАЯ ТОЧКА
геометрическая точка, обладающая массой; материальная точка — абстрактный образ материального тела, обладающего массой и не имеющего размеров. Начала современного естествознания. Тезаурус. — Ростов-на-Дону.В.Н. Савченко, В.П. Смагин.2006. смотреть
МАТЕРИАЛЬНАЯ ТОЧКА
material particle, point particle, particle* * *particle
МАТЕРИАЛЬНАЯ ТОЧКА
1) mass point2) material point3) particle4) single mass point
Материальная точка: определение, величины, примеры и решение задач
Что такое материальная точка? Какие физические величины связаны с ней, для чего вообще вводится понятие материальной точки? В этой статье мы порассуждаем об этих вопросах, приведем примеры задач, которые связаны с обсуждаемым понятием, а также поговорим о формулах, применяемых для их решения.
Определение
Итак, что же такое материальная точка? Разные источники дают определение в несколько разном литературном стиле. То же самое касается и преподавателей в вузах, колледжах и общеобразовательных учреждениях. Однако, согласно стандарту, материальной точкой называется тело, размерами которого (в сравнении с размерами системы отсчета) можно пренебречь.
Связь с реальными объектами
Казалось бы, как можно принять за материальную точку человека, велосипедиста, автомобиль, корабль и даже самолет, о которых в большинстве случаев идет речь в задачах по физике, когда речь заходит о механике движущегося тела? Давайте смотреть глубже! Для определения координаты движущегося тела в любой момент времени необходимо знать несколько параметров. Это и начальная координата, и скорость движения, и ускорение (если оно, конечно же, имеет место), и время.
Что необходимо для решения задач с материальными точками?
Координатную связь можно найти, только привязавшись к системе координат. Вот такой своеобразной системой координат для автомобиля и другого тела становится наша планета. А в сравнении с ее величиной размерами тела действительно можно пренебречь. Соответственно, если тело мы принимаем за материальную точку, ее координату в двухмерном (трехмерном) пространстве можно и нужно находить как координату геометрической точки.
Движение материальной точки. Задачи
В зависимости от сложности, задачи могут приобретать определенные условия. Соответственно, отталкиваясь от данных нам условий, можно использовать определенные формулы. Иногда, даже имея весь арсенал формул, решить задачу, что называется, «в лоб» все равно не представляется возможным. Поэтому крайне важно не просто знать формулы кинематики, имеющие отношение к материальной точке, но и уметь их использовать. То есть выражать нужную величину, а системы уравнений приравнивать. Вот основные формулы, которые мы будем применять в ходе решения задач:
Задача № 1
Автомобиль, стоящий на стартовой черте, резко начинает движение из неподвижного положения. Узнать, за какое время он разгонится до 20 метров в секунду, если его ускорение составляет 2 метра на секунду в квадрате.
Задача № 2
Материальная точка начинает экстренное торможение. Определить, какой была начальная скорость в момент экстренного торможения, если до полной остановки тела прошло 15 секунд. Ускорение принять равным 2 метрам на секунду в квадрате.
Как и в прошлый раз, сначала выразим необходимую нам величину. Чтобы избежать возни со знаками, начальную скорость оставим там, где она есть. С противоположным знаком переносим в другую часть уравнения произведение ускорения на время. Так как торможение было полным, конечная скорость составляет 0 метров в секунду. Подставляя эти и другие значения, легко находим начальную скорость. Она будет равна 30 метрам в секунду. Легко заметить, что, зная формулы, справляться с простейшими задачами не так уж и сложно.
Задача № 3
В определенный момент времени диспетчеры начинают слежение за перемещением воздушного объекта. Его скорость в этот момент равняется 180 километрам в час. Через промежуток времени, равный 10 секундам, его скорость увеличивается до 360 километров в час. Определите расстояние, пройденное самолетом за время перелета, если время полета составило 2 часа.
На самом деле в широком понимании данная задача имеет множество нюансов. Например, разгон воздушного судна. Понятно, что по прямолинейной траектории наше тело двигаться бы не могло в принципе. То есть ему нужно взлететь, набрать скорость, а потом уже на определенной высоте какой-то отрезок расстояния двигаться прямолинейно. В расчет не берутся отклонения, а также замедление самолета при посадке. Но это не наше дело в данном случае. Поэтому мы будем решать задачу в рамках школьных знаний, общих сведений о кинематическом движении. Чтобы решить задачу, нам понадобится следующая формула:
Но вот тут нас ожидает загвоздка, о которой мы говорили ранее. Знать формулы недостаточно – их нужно уметь использовать. То есть выводить одну величину при помощи альтернативных формул, находить ее и подставлять. При просмотре начальных сведений, которые имеются в задаче, сразу становится понятно, что решить ее просто так не получится. Об ускорении ничего не сказано, зато есть информация о том, как изменилась скорость за определенный промежуток времени. Значит, ускорение мы можем найти самостоятельно. Берем формулу нахождения мгновенной скорости. Она имеет вид
Ускорение и время оставляем в одной части, а начальную скорость переносим в другую. Затем делением обеих частей на время освобождаем правую часть. Здесь сразу же можно подсчитать ускорение, подставив прямые данные. Но гораздо целесообразнее выражать и дальше. Полученную для ускорения формулу подставляем в основную. Там можно немного сократить переменные: в числителе время дано в квадрате, а в знаменателе – в первой степени. Поэтому от этого знаменателя можно избавиться. Ну а дальше – простая подстановка, поскольку больше выражать ничего не надо. Ответ должен получиться следующий: 440 километров. Ответ будет другим, если переводить величины в другую размерность.
Заключение
Итак, что же мы выяснили в ходе этой статьи?
2) Для решения задач, связанных с материальной точкой, есть несколько формул (приведены в статье).
3) Знак ускорения в этих формулах зависит от параметра движения тела (ускорение или торможение).
Кинематика. Материальная точка.
Понятие «материальная точка» вводится для описания с помощью математических формул механического движения тел, поскольку описывать движение точки проще, чем реального тела, частицы которого, к тому же могут двигаться с разными скоростями.
Реальные движения тел довольно сложны, и изучая их возникает необходимость отвлечься от несущественных для данного движения деталей. С этой целью используют некоторые понятия, применимость которых определяется изучаемым движением.
Заменив тело материальной точкой, ей приписывают массу этого тела, пренебрегая его размерами, а вместе с этим и различием характеристик движения его точек.
Любое тело можно представить в виде материальной точки, если расстояния, проходимые телом, очень велики по сравнению с его размерами.
Тело, размерами которого в данных условиях движения можно пренебречь, называют материальной точкой. Слова «в данных условиях» означают, что при одних движениях тело можно считать материальной точкой, а при других – нет. Например, планеты при изучении их движения вокруг Солнца считаются материальными точками. Однако, решая задачи, связанные с суточным вращением планет, считать планеты материальными точками уже нельзя.
При поступательном движении тела, даже если его размеры сопоставимы с расстоянием, которое оно проходит, тело можно рассматривать в качестве материальной точки, поскольку все его точки движутся одинаково.
МАТЕРИАЛЬНАЯ ТОЧКА
МАТЕРИАЛЬНАЯ ТОЧКА, вводимое в механике понятие об объекте исчезающе малых размеров, имеющем массу. Положение М. т. в пространстве определяется как положение геометрич. точки, что существенно упрощает решение задач механики. Практически данное тело можно рассматривать как М. т. в случаях, когда оно движется поступательно или когда расстояния, проходимые точками тела, очень велики по сравнению с его размерами. При движении любой меха-нич. системы (в частности, твёрдого тела) её центр масс (центр тяжести) движется так же, как двигалась бы М. т. с массой, равной массе всей системы, под действием всех внешних сил, приложенных к системе.
Материальная точка — масса, которую мы воображаем сосредоточенной в одной геометрической подвижной точке. Назначение материальной точки в механике состоит в том, чтобы заменять собой такие тела, размерами которых мы пренебрегаем сравнительно с длинами, рассматриваемыми в данном вопросе. Напр. в тех вопросах астрономии, в которых не принимаются в расчет вращательные движения светил около их осей, каждое светило заменяется точкой, масса которой равна массе светила.
— понятие, вводимое в механике для объекта бесконечно малых размеров, имеющего массу. Положение M. т. в пространстве определяется как положение геом. точки, что существенно упрощает решение задач механики. Практически всякое тело можно рассматривать как M. т. в случаях, когда расстояния, проходимые точками тела, очень велики по сравнению с его размерами. Кроме того, при изучении движения любой механич. системы (в частности, ц твёрдого тела) закон движения её центра масс (центра тяжести) находится как закон движения M. т., имеющей массу, равную массе системы, и находящейся под действием всех внеш. сил, приложенных к системе.