Что измеряют с помощью линейки
Измерения с помощью линейки
Обработка экспериментальных данных.
Притчи Соломона 20:23
Введение.
Изучать природные явления можно двумя способами: качественно и количественно. В первом случае можно сделать выводы только о связи одних природных явлений с другими. Во втором случае необходимо получить аналитическую зависимость нескольких физических величин, т.е. поставить в соответствие численные значения этих величин.
Например, изучая падение тел с высоты, можно сделать простой вывод о том, что любые тела, отпущенные без начальной скорости, упадут на землю, причем их движение будет происходить по вертикали, а если тело бросить под углом к поверхности земли, то оно тоже упадет, но будет двигаться по более сложной траектории. Это качественный вывод, потому что мы не оцениваем, например, время падения, не исследуем зависимость этого времени от массы тела или температуры воздуха, не задаемся целью найти форму трактории (оказывается, в вакууме при небольщих высотах подъема это будет парабола!).
Другим примером качественного вывода служит утверждение, что при приближении постоянного магнита к замкнутому проводящему контуру в нем начинает течь ток. Это – явление электромагнитной индукции. Углубляясь в подробности, можно заметить связь между направлением тока в контуре и тем, какой полюс магнита приближается к контуру. Такую зависимость можно объяснить правилом Ленца. Опять же это всего лишь качественные выводы без дополнительной информации о зависимости силы тока в контуре, например, от скорости приближения магнита.
Для количественного изучения явлений нам необходимо получить численную взаимосвязь между физическими величинами. Рассмотрим первый пример, где тело падает по вертикали без начальной скорости. Чтобы не обсуждать воздействие воздуха, придется проводить опыты в вакууме. Найдем времена падения тела 
при разных высотах 
и убедимся в в том, что существует зависимость между этими двумя физичискими величинами: 
,
причем самый интересный численный вывод заключается в том, что
,
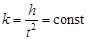
т.е. этот коэффициент не зависит от размеров или массы тела. Но такая простота исчезает, когда мы проделаем те же опыты в воздухе. Сказывается сопротивление воздуха, которое явно зависит от размеров и формы тела (явно для тех, кто догадается для опытов подобрать тела разных размеров, но обязательно одинаковых масс). Таким образом, количественное изучение сопротивления воздуха дает конструкторам направление поисков, например, для разработки формы крыла самолета, испытывающего наименьшее сопротивление.
Измерительные приборы
Выполняя лабораторные работы в курсах разных дисциплин, и конечно же при изучении курса общей физики, в большинстве случаев необходимо получить количественный вывод о явлениях, т.е. найти численное значение, например, силы трения, коэффициента упругости пружины, динамического коэффициента вязкости, ускорения свободного падения и т.д. Немного реже требуется подтвердить теоретическую зависимость одной величины от другой, например, линейную зависимость сопротивления металла от температуры или линейную зависимость углового ускорения вращающегося тела от приложенного к нему момента силы, нелинейную зависимость тока в туннельном диоде от напряжение на нем и.т.д.
В любом случае, Экспериментатору (назовем этим звучным словом студента при выполнении лабораторной работы) требуются приборы, которые помогут ему измерить различные физические величины. Обычно набор приборов невелик: для механических опытов это
— линейка для измерения размеров тел и расстояний между точками (а еще с помощью этой же линейки можно проводить карандашом линии на графике!);
— штангенциркуль и микрометр для измерения размеров тел любой формы, например, диаметр шара или цилиндра, а также для более точного измерения малых размеров;
— секундомер для измерения временной длительности процессов (время падения, время колебаний, время вытекания воды из сосуда);
— весы для измерения массы тел (не мешало бы иметь в лаборатории). Как показывает практика, все используемые в лабораторных работах тела взвешены лаборантом и Экспериментатор уже имеет численные значения масс, нанесенные обычно прямо на поверхность этих тел разными способами – или краской или механическим продавливанием.
Для лабораторных работ по электричеству и магнетизму нужны
— амперметр, измеряющий ток;
— вольтметр, измеряющий напряжение.
— осциллограф, который помогает изучать электрические процессы во времени.
 |
2.1. Приборы, измеряющие линейные размеры
Рис.1. Штангенциркули а) и в); стальная линейка б); микрометр г)
Как видно из рис.1, на каждом из приборов есть набор тонких линий, повторяющихся через одинаковый интервал, а также целые числа. На основной шкале штангенциркулей и линейке (рис.1. а, б, в) числа выражают сантиметры. Между двумя числами ровно 10 интервалов по одному миллиметру. Такая линейка называется миллиметровой. Говорят, что цена деления линейки равна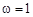 
мм (насчет штангенциркулей разговор особый). Для удобства отсчетов каждая пятая линия рисуется длиннее других, а каждая десятая еще длиннее.
Измерения с помощью линейки
Чтобы измерить ширину 
деревянного бруска линейкой, нам необходимо приложить ее нулевую линию с левым краем бруска. В нашем примере (см. рис.2) нулевая линия совпадает с левым краем самой линейки, что очень удобно, потому что можно совместить края бруска и линейки наощупь (такое расположение нулевой линии достаточно редко, и обычно она рисуется на удалении в несколько миллиметров от левого края линейки). Правый край бруска располагается между двумя линиями на линейке, что соответствует значению 
мм.
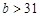
Можно гордо заявить, что ширина бруска 
мм, но это будет все равно не точный ответ. Чтобы не спорить о том, кто точнее может измерять размеры тел с помощью линейки и у кого глаз-алмаз, принято формально приписывать каждому прибору погрешность измерения.
Не вдаваясь в точную теорию погрешностей, для простоты расчетов примем погрешность прибора при однократном измерении как половину цены его деления и обозначим так: 
. Для миллиметровой линейки погрешность составит полмиллиметра, т.е 
мм. Как же тогда записать в толстую лабораторную тетрадь результат этого важного эксперимента по измерению ширины бруска? Очень просто:
мм.
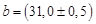
Для более щепетильных в вопросе точности можно предложить такую запись:
мм
Рис.2. Измерение ширины деревянного бруска. У левого края линейки двумя буквами «мм» отмечено то, что линейка миллиметровая.
Две приведенные записи ответа означают следующее: точное значение ширины бруска не известно, но с уверенностью можно сказать (вот только на сколько процентов эта уверенность?), что оно лежит в диапазоне между 30,5 мм и 31,5 мм для первой записи или в диапазоне от 31,0 мм до 32,0 мм для второй. И какая запись более правильная? Вторая более наглядна, а посему примем ее за эталон. И вообще, оставим право округлять ответ до ближайшего деления на линейке или не округлять Экспериментатору, ведь глаз человека очень точный прибор. Он различает размеры меньше толщины волоса, которая составляет всего несколько микрометров (см. рис.10Б), а уж размер в полмиллиметра и подавно.
Если точность измерения ширины брусков мм при изготовлении стропил для строительства новой крыши превышает все запросы дачника, то изготовление цилиндрической втулки требует для измерения ее диаметра 
большей точности, например, 
мм или даже 
мм. Если диаметр втулки сделать на 0,1 мм больше, то она может не зайти в нужное отверстие, если на 0,1 мм меньше, то она будет в отверстии немного болтаться, что в конечном итоге вызовет поломку механизма. Измерять с такой точностью призван штангенциркуль (рис.3)
Измерительные линейки, штангенинструмент и микрометрические инструменты
Измерительные линейки, штангенинструмент и микрометрические инструменты
Измерительные линейки
Измерительные линейки (рис. 1.7) относятся к штриховым мерам и предназначены для измерения размеров изделий 14. 18 квалитетов точности прямым методом.
Они предназначены для измерений высот, длин, диаметров, глубин в различных отраслях промышленности, в том числе и в машиностроении. Их основное преимущество — простота конструкции, низкая стоимость, надежность и простота в измерении. Измерение производят прикладыванием линейки к измеряемому объекту, чаще всего совмещая нулевой штрих линейки с краем детали. Отсчет по шкале на другом краю детали дает искомый результат измерения. Но это не обязательно. Так, например, при измерении диаметра отверстия снимаются два показания: с одной стороны отверстия и с другой. Вычитая из большего значения меньшее, получаем размер диаметра.
Конструкции линеек однотипны. Они представляют собой металлическую полосу шириной 20. 40 мм и толщиной 0,5. 1,0 мм, на широкой поверхности которой нанесены деления. Линейки изготавливают с одной или двумя шкалами, с верхними пределами измерений 150, 300, 500 и 1 000 мм и ценой деления 0,5 или 1 мм. Линейки с ценой деления 1 мм могут иметь на длине 50 мм от начала шкалы полумиллиметровые деления.
Рис. 1.7. Линейки металлические
Допускаемые отклонения действительной общей длины шкалы линеек от номинального значения находятся в пределах +(0,10. 0,20) мм в зависимости от общей длины шкалы, а отдельных подразделений— не более ±(0,05. 0,10) мм.
Поверку (калибровку) линеек, т. е. определение погрешности нанесения штрихов, производят по образцовым измерительным линейкам, которые называются штриховыми мерами. Погрешность такого сравнения не превышает 0,01 мм.
Штангенинструмент
Предназначен для абсолютных измерений линейных размеров наружных и внутренних поверхностей, а также для воспроизведения размеров при разметке деталей.
К нему относятся штангенциркули (рис. 1.8), штангенглубино- меры и штангенрейсмасы.
Основными частями штангенциркуля являются штанга-линейка с делениями шкалы 1 мм и перемещающаяся по линейке шкала-нониус 5. По штанге-линейке отсчитывают целое число миллиметров, а по нониусу— десятые и сотые доли миллиметра.
По основной линейке 1 с неподвижными губками 2 перемещается рамка 3 с подвижными измерительными губками. Для плавного перемещения рамки по штанге-линейке предусмотрено микрометрическое устройство 7, состоящее из хомутика, зажима и гайки микрометрической подачи. На подвижной рамке установлен стопорный винт 4. Для измерения глубины отверстий пазов и других внутренних элементов деталей используется линейка глубиномера 6.
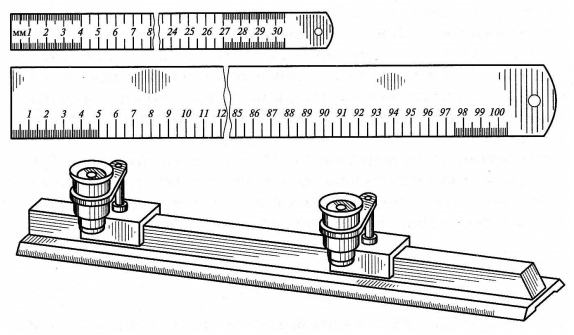
Для отсчета с помощью нониуса сначала определяют по основной шкале целое число миллиметров перед нулевым делением нониуса. Затем добавляют к нему число долей по нониусу в соответствии с тем, какой штрих шкалы нониуса ближе к штриху основной шкалы (рис. 1.8, г).
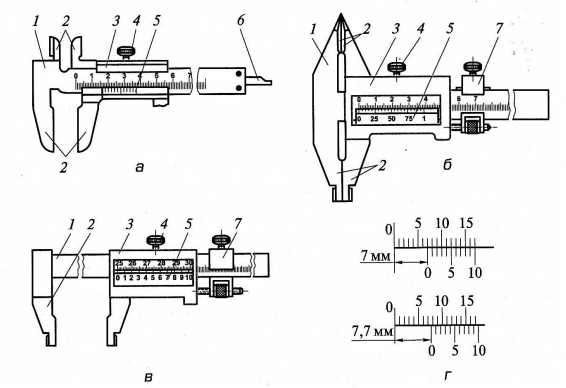
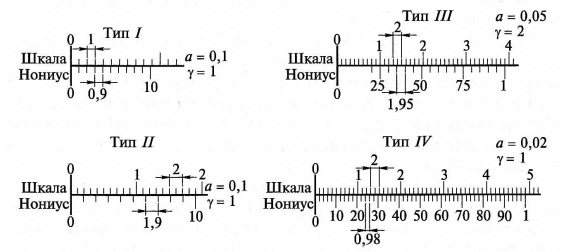
Основные типы нониусов (I—IV) представлены на рис. 1.9.
Основными характеристиками нониуса являются величина отсчета по нониусу (цена деления нониуса) а и модуль нониуса у, которые определяются по следующим формулам:
где i — цена деления основной шкалы, мм; n — число делений нониуса; l — длина шкалы нониуса мм.
Рис. 1.8. Конструкция штангенциркулей:
а — типа ШЦ-1; б — типа ШЦ-П; в — типа ШЦ-Ш; г — отсчет по нониусу; 7 — штанга-линейка; 2 — измерительные губки; 3 — рамка; 4 — винт зажима рамки; 5 — нониус; 6 — линейка глубиномера; 7 — рамка микрометрической подачи
Наибольшее распространение получили нониусы с точностью отсчета 0,1; 0,05; 0,02 мм. Основные метрологические характеристики штангенинструментов, применяемых в машиностроении, представлены в табл. 1.2.
ГОСТ 166—89 предусматривает изготовление и использование трех типов штангенциркулей: ШЦ-1 с ценой деления 0,1 мм, ШЦ-П с ценой деления 0,05 мм и 0,1 мм, ШЦ-Ш с ценой деления 0,05 и 0,1 мм. Кроме того, на заводах применяют ранее изготовленные штангенциркули с ценой деления нониуса 0,02 мм, а также индикаторные штангенциркули с ценой деления индикатора 0,1; 0,05; 0,02 мм.
В штангу индикаторного штангенциркуля (рис. 1.10) вмонтирована зубчатая рейка 2, по которой перемещается зубчатое колесо 3 индикатора, закрепленного на рамке 1. Перемещение зубчатого колеса передается на стрелку индикатора, показывающую единицы, десятые и сотые доли миллиметра.
Для линейных измерений в последнее время применяют также штангенинструменты с электронным цифровым отсчетом (рис. 1.11). В этих приборах вдоль штанги также располагается многозначная мера, по которой отсчитывается величина перемещения подвижной рамки. В качестве многозначной меры используются фотоэлектрические или емкостные преобразователи. Большинство штангенинструментов с электронным отсчетным устройством имеют возможность представления результата измерения непосредственно на шкалу прибора либо на подключаемый к нему микропроцессор. Цена деления таких приборов составляет 0,01 мм.
Штангенглубиномеры (ГОСТ 162 — 90) (рис. 1.12) принципиально не отличаются от штангенциркулей и применяются для измерения глубины отверстий и пазов. Рабочими поверхностями штангенглубииомеров являются торцовая поверхность штанги-линейки 1 и база для измерений — нижняя поверхность основания 4. Для удобства отсчета результатов измерений, повышения точности и производительности контрольных операций в некоторых типах штангенглубииомеров вместо нониусной шкалы предусматривается установка индикатора часового типа с ценой деления 0,05 и 0,01 мм.
Штангенрейсмасы (ГОСТ 164—90) (рис. 1.13) являются основными измерительными инструментами для разметки деталей и определения их высоты. Они могут иметь дополнительный присоединительный узел для установки измерительных головок параллельно или перпендикулярно плоскости основания.
Рис. 1.9. Типы нониусов
Могу ли я в своем швейном деле применять мерки на глаз?
