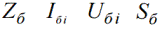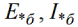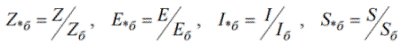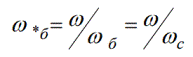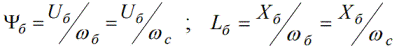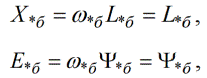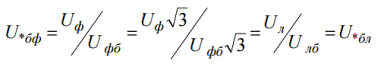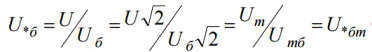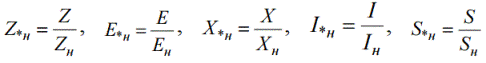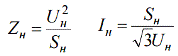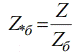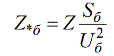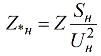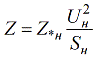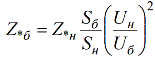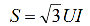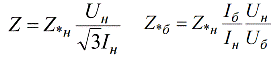Абсолютные и относительные статистические величины

Понятие абсолютных величин

Абсолютные величины — это результаты статистических наблюдений. В статистике в отличие от математики все абсолютные величины имеют размерность (единицу измерения), а также могут быть положительными и отрицательными.

Единицы измерения абсолютных величин отражают свойства единиц статистической совокупности и могут быть простыми, отражая 1 свойство (например, масса груза измеряется в тоннах) или сложными, отражая несколько взаимосвязанных свойств (например, тонно-километр или киловатт-час).

Единицы измерения абсолютных величин могут быть 3 видов:

Абсолютные величины могут быть моментными или интервальными. Моментные абсолютные величины показывают уровень изучаемого явления или процесса на определенный момент времени или дату (например, количество денег в кармане или стоимость основных фондов на первое число месяца). Интервальные абсолютные величины — это итоговый накопленный результат за определенный период (интервал) времени (например, зарплата за месяц, квартал или год). Интервальные абсолютные величины, в отличие от моментных, допускают последующее суммирование.

Абсолютная статистическая величина обозначается X, а их общее число в статистической совокупности — N.

Количество величин с одинаковым значением признака обозначается f и называется частота (повторяемость, встречаемость).

Cами по себе абсолютные статистические величины не дают полного представления об изучаемом явлении, так как не показывают его динамику, структуру, соотношение между частями. Для этих целей служат относительные статистические величины.

Понятие и виды относительных величин

Относительная статистическая величина — это результат соотношения двух абсолютных статистических величин.

Если соотносятся абсолютные величины с одинаковой размерностью, то получаемая относительная величина будет безразмерной (размерность сократится) и носит название коэффициент.

Часто применяется искусственная размерность коэффициентов. Она получается путем их умножения:

Искусственная размерность коэффициентов применяется, как правило, в разговорной речи и при формулировании результатов, а в самих расчетах она не используется. Чаще всего применяются проценты, в которых принято выражать полученные значения относительных величин.

Чаще вместо названия относительная статистическая величина используется более краткий термин-синоним — индекс (от лат. index — показатель, коэффициент).

В зависимости от видов соотносимых абсолютных величин при расчете относительных величин, получаются разные виды индексов: динамики, планового задания, выполнения плана, структуры, координации, сравнения, интенсивности.

Индекс динамики

Индекс динамики (коэффициент роста, темп роста) показывает во сколько раз изменилось изучаемое явление или процесс во времени. Рассчитывается как отношение значения абсолютной величины в отчетный (анализируемый) период или момент времени к базисному (предыдущему):

.

Здесь и далее подиндексы означают: 1 — отчетный (анализируемый) период, 0 — базисный (прошлый) период.

Индекс планового задания

Индекс планового задания – это отношение планового значения абсолютной величины к базисному:

Например, автосалон в январе продал 100 автомобилей, а на февраль запланировал продать 120 автомобилей. Тогда индекс планового задания составит i пз = 120/100 = 1,2, что означает планирование роста продаж в 1,2 раза или на 20%

Индекс выполнения плана

Индекс выполнения плана – это отношение фактически полученного значения абсолютной величины в отчетном периоде к запланированному:

Например, автосалон в феврале продал 110 автомобилей, хотя на февраль было запланировано продать 120 автомобилей. Тогда индекс выполнения плана составит i вп = 110/120 = 0,917, что означает выполнение плана на 91,7%, то есть план недовыполнен на (100%-91,7%) = 8,3%.

Перемножая индексы планового задания и выполнения плана, получим индекс динамики:

В рассмотренном ранее примере про автосалон, если перемножим полученные значения индексов планового задания и выполнения плана, то получим значение индекса динамики: 1,2*0,917 = 1,1.

Индекс структуры

Индекс структуры показывает, какую долю составляет отдельная часть совокупности от всей совокупности.

Например, если в рассматриваемой группе студентов 20 девушек и 10 молодых людей, тогда индекс стурктуры (доля) девушек будет равен 20/(20+10) = 0,667, то есть доля девушек в группе составляет 66,7%.

Индекс координации

Индекс координации показывает, во сколько раз больше или сколько процентов составляет одна часть статистической совокупности по сравнению с другой ее частью, принятой за базу сравнения.

Например, если в группе студентов из 20 девушек и 10 молодых людей, принять за базу сравнения численность девушек, тогда индекс координации численности молодых людей составит 10/20 = 0,5, то есть численность молодых людей составляет 50% от численности девушек в группе.

Индекс сравнения

где А, Б — признаки сравниваемых объектов или территорий.

Индекс интенсивности

Например, хлебный магазин продал 500 буханок хлеба и заработал на этом 10000 руб., тогда индекс интенсивности составит 10000/500 = 20 [руб./бух.хлеба], то есть цена продажи хлеба составила 20 руб. за буханку.

Большинство величин с дробной размерностью представляют собой индексы интенсивности.

Источник

Система относительных единиц

Для упрощения вычислений при расчетах параметров в системах передачи электроэнергии, применяют систему относительных единиц. Этот способ подразумевает выражение текущего значения системной величины через принятую за единицу базовую (базисную) величину.

Так, относительная величина выражается как множитель базового значения (тока, напряжения, сопротивления, мощности и т. д.), и не зависит, будучи выражена в относительных единицах, от уровня напряжения. В англоязычной литературе относительные единицы обозначаются pu или p.u. (от per-unit system — система относительных единиц).

Например, для однотипных трансформаторов, падение напряжения, импеданс и потери отличаются при разном подаваемом напряжении по абсолютной величине. Но по относительной величине они будут оставаться примерно одинаковыми. Когда расчет произведен, то результаты легко переводятся обратно в системные единицы (в амперы, в вольты, в омы, в ватты и т. д.), поскольку базисные величины, с которыми сравнивали текущие значения, известны изначально.

Как правило, относительные единицы удобны при расчетах передаваемой мощности, но часто бывает, что параметры генераторов моторов и трансформаторов указываются и в относительных единицах, поэтому каждому инженеру следует быть знакомым с концепцией относительных единиц. Единицы мощности, силы тока, напряжения, импеданса, адмиттанса — используются в системе относительных единиц. Мощность и напряжение являются независимыми величинами, это продиктовано свойствами реальных энергосистемам.

Все системные сетевые величины могут быть выражены как множители выбранных базисных значений. Так, если говорить о мощности, то в качестве базисной величины можно выбрать номинальную мощность трансформатора. Бывает, что мощность, полученная в конкретный момент времени в виде относительного значения сильно облегчает вычисления. Базис для напряжения — номинальное напряжение шины и т. д.

Вообще, контекст всегда позволяет понять, о какой относительной величине идет речь, и даже наличие одного и того же символа «pu» в англоязычной литературе не будет вас смущать.

Итак, все системные физические величины являются именованными. Но при переводе их в относительные единицы (по сути — в проценты), характер теоретических выкладок обобщается.

Под относительным значением какой-нибудь физической величины понимается ее отношение к некоторому базовому значению, то есть к значению, выбранному за единицу при данном измерении. Относительная величина обозначается символом звездочки снизу.

Часто при расчетах в качестве базисных величин принимают: базисное сопротивление, базисный ток, базисное напряжение и базисную мощность.

Нижний индекс «б» обозначает, что это базисная величина.

Тогда относительные единицы измерения будут называться относительными базисными:

К примеру, для измерения угловых скоростей, за единицу принимают угловую синхронную скорость, и значит угловая скорость синхронная будет равна угловой скорости базисной.

А произвольная угловая скорость тогда может быть выражена в относительных единицах:

Соответствующим образом в качестве базисных могут быть приняты для потокосцепления и для индуктивности следующие соотношения:

Здесь базисное потокосцепление — потокосцепление, индуцирующее базисное напряжение при базисной угловой скорости.

Так, если синхронная угловая скорость принята за базис, то:

в относительных единицах ЭДС равно потокосцеплению, а индуктивное сопротивление равно индуктивности. Так получается потому, что базисные единицы выбраны соответствующим образом.

Далее рассмотрим в относительных и базисных единицах фазное напряжение:

Легко видеть, что фазное напряжение в относительных базисных единицах оказывается равным линейному относительному базисному напряжению. Аналогичным образом и амплитудное значение напряжения в относительных единицах оказывается равным действующему:

Важно здесь отметить, что и для любого элемента электрической цепи, относительное сопротивление будет равно относительному падению напряжения в условиях номинальной мощности, подаваемой в цепь.

При расчетах токов короткого замыкания, пользуются четырьмя базисными параметрами: ток, напряжение, сопротивление и мощность. Базисные значения напряжения и мощности принимают независимыми, и через них потом выражают базисные сопротивление и ток. Из уравнения мощности трехфазной сети — ток, затем по закону Ома — сопротивление:

Так как базисная величина может быть выбрана произвольно, то одна и та же физическая величина может, при выражении ее в относительных единицах, иметь различные числовые значения. Относительные сопротивления генераторов, двигателей, трансформаторов, задаются поэтому в относительных единицах посредством введения относительных номинальных единиц. Sн — номинальная мощность. Uн — номинальное напряжение. А относительные номинальные величины записываются с нижним индексом «н»:

Для нахождения номинальных сопротивлений и токов применяют стандартные формулы:

Чтобы установить связь между относительными единицами и именованными величинами, сначала выразим связь между относительной базисной и базисной величинами:

Распишем базовое сопротивление через мощность, и подставим:

Так можно перевести именованную величину в относительную базисную.

И аналогичным образом можно установить связь между относительными номинальными единицами и именованными:

Для вычисления сопротивления в именованных единицах при известных относительных номинальных, используют следующую формулу:

Связь между относительными номинальными единицами и относительными базисными единицами устанавливает следующая формула:

При помощи этой формулы относительные номинальные единицы можно перевести в относительные базисные единицы.

В энергосистемах с целью ограничения токов короткого замыкания устанавливают токоограничительные реакторы, по сути — линейные индуктивности. Для них задаются номинальные напряжение и ток, но не мощность.

и преобразовав приведенные выше выражения для относительного номинального и относительного базового сопротивлений, получим:

Могут быть выражены относительные величины и в процентах:

Источник

Использование относительных единиц при расчете систем электроприводов

При различного рода расчетах нам иногда приходится сталкиваться с таким понятием как относительные единицы или в процентах. Они довольно часто используются при расчетах, где часто нужно проводить сравнение элементов с различными номинальными данными. Давайте рассмотрим что такое относительные единицы на примере системы электропривода.

Не всегда полученные непосредственные результаты могут служить объективным критерием для оценки преимуществ и недостатков сравниваемых вариантов. К примеру анализ пускового тока двигателей постоянного тока с различным номинальным напряжением не сможет дать точный ответ где условия пуска будут легче. Соответственно нельзя сделать заключение о величине пусковых сопротивлений на каждой ступени. Для избежания неопределенности целесообразней проводить расчеты не в абсолютных единицах (Вольты, Амперы и т.д.), а в относительных. Это позволит не проводит переходы от одних единиц к другим, от одних измерений к другим, а с помощью специально построенных кривых определять параметры двигателя непосредственно (необходимые для построения характеристик двигателя).

Чтобы выразить величину в относительных единицах необходимо ее абсолютное значение отнести к аналогичной величине, принятой за единицу.

Выбираться величины могут произвольно, но для систем электроприводов обычно используют номинальные: U_ном – напряжение, I_ном — ток, M_ном — момент, r_ном – сопротивление обмоток, n_ном – обороты вала (об/мин).

Для асинхронных и синхронных электродвигателей n_о – скорость вращения магнитного потока статора. Если рассматривается двигатель постоянного тока независимого возбуждения, то для данного типа двигателя n_о – скорость идеального холостого хода.

Для удобства обозначения параметр в относительных единицах будет обозначаться той же буквой, но с индексом о.е. или для соотношения величины в процентах %.

Напряжение в относительных единицах и процентах:

В асинхронных двигателях различают два напряжения номинальных: 1 – линейное статора, 2 – ЭДС неподвижного ротора.

Ток в о.е. и процентах:

В асинхронных машинах под номинальным роторным сопротивлением понимают сопротивление каждой фазы роторной обмотки (вместе с добавочным сопротивлением, если используется машина с фазным ротором). Полное номинальное сопротивление ротора при соединении обмоток в звезду:

Соотношение для сопротивлений ротора в случае соединения звездой:

Соответственно значение момента электромашины в о.е. и %:

Скорость вращения вала в о.е. и %:

Так как скорость идеального холостого хода стремится к бесконечности в таких машинах постоянного тока как последовательного и смешанного возбуждения, то для расчета скорости в о.е. и % за единицу измерения принимают скорость номинальную двигателя:

Скольжение асинхронных машин может быть выражено тоже через скорость в о.е. и процентах:

Источник

Система относительных единиц

Представление любых физических величин не в обыч­ных для них соответствующих именованных единицах, а в относительных, безразмерных единицах позволяет существенно упростить некоторые теоретические вы­кладки и придать им более общий характер. Равным образом и в практических расчетах такое представление величин придает результатам большую наглядность и по­зволяет быстрее ориентироваться в порядке определяе­мых значений. Благодаря этому система относительных единиц широко используется, хотя на первый взгляд она может казаться несколько искусственной и даже излиш­ней.

С выражением величин в относительных единицах (в долях или процентах) читатель уже встречался при изучении электрических машин, где реактивности обычно выражают в долях единицы, напряжения короткого за­мыкания трансформаторов—в процентах, пусковые токи и моменты асинхронных двигателей—в кратностях от их номинальных значений и т. д. Теперь нам нужно по­знакомиться с системой относительных единиц в более широком аспекте, имея в виду использование ее при решении различных вопросов и задач для схем с произ­вольным числом всевозможных элементов.

Напомним, что под относительным значением какой-либо величины следует понимать ее отношение к другой одноименной величине, выбранной за единицу измерения. Следовательно, чтобы выразить отдельные величины в относительных единицах, нужно прежде всего выбрать те величины, которые должны служить соответственны­ми единицами измерения, или, как говорят, установить базисные единицы (или условия).

Пусть за базисный ток и базисное междуфазное на­пряжение приняты некоторые произвольные величины I_б и U_б. Тогда базисная мощность трехфазной системы, оче­видно, будет:

и базисное сопротивление

z_б= (2-2)

т. е. оно подчинено закону Ома, чтобы обеспечить тож­дественную запись этого закона как в именованных, так и в относительных единицах.

Как видно, из четырех базисных единиц I_б, U_б, S_б и z_б только две могут быть выбраны произвольно, а две другие уже получаются из указанных соотношений. Фаз­ные и междуфазные базисные напряжения, а также фазные и линейные базисные токи связаны между собой известными соотношениями для симметричной трехфаз­ной системы. Следует особо подчеркнуть, что выбранные базисные единицы служат для измерения как полных ве­личин, так и их составляющих (активных, реактивных и пр.).

Таким образом, при выбранных базисных условиях относительные значения э. д. с., напряжения, тока, мощ­ности и сопротивления будут:

=E/U_б (2-3)

=U/U_б; (2-4)

=I/I_б; (2-5)

=S/S_б; (2-6)

= z/z_б, (2-7)

где звездочка указывает, что величина выражена в от­носительных единицах, а индекс (б) —что она приведе­на к базисным условиям. Эти индексы, как и многие другие, часто опускают, если смысл выражения ясен из текста.

Относительные фазные и междуфазные напряжения численно одинаковы; равным образом численно одинако­вы относительные фазная мощность и мощность трех фаз.

Используя (2-2), можно формальное определение от­носительного сопротивления по (2-7) представить в ином виде:

(2-8)

(2-9)

где z—заданное сопротивление, ом на фазу;

I_б — базисный ток, ка (а);

U_б—базисное междуфазное напряжение, кв (в);

S_б—базисная мощность, Мва (ва).

Из последних выражений следует, что относительное сопротивление численно равно относительному падению напряжения в данном элементе при протекании через не­го принятого базисного тока (или мощности).

Поскольку выбор базисных условий произволен, то одна и та же действительная величина может иметь раз­ные численные значения при выражении ее в относитель­ных единицах. Обычно относительные сопротивления

элементов задаются при номинальных условиях (т. е. при I_H или S_H и U_H). Их величины определяются по (2-8) и (2-9), где базисные единицы должны быть заменены со­ответственными номинальными,т. е.

(2–8a)

(2-9a)

Иногда относительные величины выражают не в до­левых единицах, а в процентах. Связь между такими вы­ражениями очевидна; так, например,

Активное сопротивление трансформатора весьма мало. Поэтому, пренебрегая им, можно считать, что задаваемое в процентах напряжение короткого замыкания трансформа­тора u_K% =z_%»x_%. Если при этом принять, что индуктивное сопротивление рассеяния трансформатора прибли­женно изменяется пропорционально квадрату числа вит­ков его обмоток (что довольно близко к действительно­сти), то заданное значение u_K%, следует считать от на­пряжения холостого хода того ответвления регулируемой обмотки, которое установлено у трансформатора.

Для выполнения расчета в относительных единицах нужно все э. д. с. и сопротивления элементов схемы вы­разить в относительных единицах при выбранных базис­ных условиях. Если они заданы в именованных едини­цах, то для перевода их в относительные единицы слу­жат выражения (2-3), (2-8) или (2-9). Когда же они за­даны в относительных единицах при номинальных усло­виях, то их пересчет к базисным условиям нужно произ­водить по следующим очевидным соотношениям:

(2-11)

(2-12)

(2-13)

При выборе базисных условий следует руководство­ваться соображениями, чтобы вычислительная работа была по возможности проще и порядок числовых значе­ний относительных базисных величин был достаточно удобен для оперирования с ними. Для базисной мощно­сти S_б целесообразно принимать простое круглое число (1 000 Мва, 100 Мва и т. п.), а иногда часто повторяю­щуюся в заданной схеме номинальную мощность (или кратную ей). За U_б рекомендуется принимать U_Н или близкое к нему. При U_б=U_H пересчет относительных э. д. с. вообще отпадает ( ), а выражения для пересчета относительных сопротивлений принимают бо­лее простой вид:

(2-12а)

(2-13а)

Равенство U_б=U_Н, вообще говоря, соблюдается толь­ко для части элементов, так как напряжения U_Н элемен­тов одной и той же электрической цепи в общем случае могут быть неодинаковы. Однако это различие сравни­тельно мало (в пределах ±10%) и в приближенных рас­четах им часто пренебрегают, полагая U_H всех элемен­тов одной ступени напряжения одинаковыми и равными некоторому среднему номинальному напряжению U_CP для этой цепи (см. § 2-4). Исключение целесообразно делать для реакторов, поскольку они составляют обычно значительную часть общего сопротивления цепи, опре­деление которого всегда желательно производить с боль­шей точностью. В тех случаях, когда реакторы исполь­зованы на напряжениях ниже их номинальных напряже­ний (например, реактор 10 кв в установке 6 кв и т. п.), пересчет их относительных сопротивлений по напряже­ниям, конечно, обязателен.

Пример 2-1. Асинхронный двигатель АД через кабель Кб и реактор Р присоединен к шинам (рис. 2-1), напряжение на которых поддерживается практически неизменным и равным 6,3 кв. Опреде­лить величины тока и момента при пуске этого двигателя, выразив их в долях от его соответствующих номинальных величин.

Данные: асинхронный двигатель АД 2 500 квт, 6 кв, cosj=0,9, h=96%, пуск=5,6, пуск.н=0,9. Реактор Р—10 кв, 400 а, x_%=3%. Кабель Кб— 1,25 км, х=0,071 om/km.

Примем за базисные величины номинальные данные двигателя, т. е.

U_б=6кв. S_б = = 2 900 ква

I_б= =280 а

Относительная реактивность двигателя при пуске составляет:

Рис. 2-1. Схема к примеру 2-1.

Относительные базисные реактивности реактора и кабеля будут:

x_P= =0,035

x_Кб=0,071×1,25 =0,007.

Относительное базисное напряжение на шинах источника состав­ляет:

=1,05

Искомая величина пускового тока будет:

= 4,74.

Для определения пускового момента предварительно находим напряжение у двигателя при пуске:

= 4,74×0,18 = 0,85;

следовательно, искомый пусковой момент составляет:

= 0,85 2 ×0,9 = 0,648.

Выше рассмотрены величины, с которыми преимуще­ственно приходится оперировать при выполнении обычных электрических расчетов.

Однако, как отмечалось ра­нее, в системе относительных единиц можно выразить любые физические величины, в том числе и неэлектриче­ские. Остановимся на определении относительных значе­ний тех величин, с которыми придется иметь дело в даль­нейшем.

За единицу измерения угловых скоростей обычно при­нимают синхронную угловую скорость w_С т.е. w_б = w_С. Тогда произвольная угловая скорость в относительных базисных единицах будет:

(2-14)

Соответственно этому в качестве базисных единиц при­нимают:

L_б=

Y_б=

т. е. потокосцепление, индуктирующее при базисной угло­вой скорости базисное напряжение.

Таким образом, при указанных базисных единицах и сохранении угловой скорости неизменной и равной син­хронной, очевидно, имеем:

; (2-15)*

(2-16)

. (2-17)

т. е. при этих условиях индуктивное сопротивление чис­ленно равно индуктивности, а потокосцепление численно равно э. д. с. или соответствующему падению напряже­ния.

Подобная возможность замены одних относительных величин численно равными им другими представляет одно из существенных достоинств системы относительных единиц.

* Вместо индуктивности L здесь может бытьтакже взаимная индуктивность М.

дуги отвечает требованиям к разрядному сопротивле­нию для осуществления оптимальных условий гашения. Поскольку падение напряжения на короткой дуге со­ставляет всего лишь около 30 в, для гашения поля при более высоких напряжениях авторами предложено при­менять последовательное соединение ряда коротких дуг, что выполнено в дугогасящей решетке (ДГР).

Дугогасящая решетка может быть включена парал­лельно обмотке возбуждения (рис. 8-7,а) или после­довательно с ней 1 (рис. 8-7,6).

В первом случае контак­ты 2 (агп) в нормальных условиях замкнуты, а кон­такты 1—разомкнуты. При действии АГП сначала за­мыкаются контакты 1 и шун­тируют через сопротивле­ние r‘ обмотку возбуждения. Затем происходит размыка­ние контактов 2 и через ма­лый интервал контактов 1. Возникшая при этом на кон­тактах 1 дуга под влиянием специально созданного маг­нитного поля увлекается в решетку, где, разбившись

на ряд коротких дуг, она продолжает гореть до пре­кращения тока. Небольшое сопротивление r‘ введено для того, чтобы при замыкании контактов 1 возбуди­тель не оказался закороченным.

При последовательном включении дугогасящей решетки (рис. 8-7,6) контакты 1(АГП) в нормальных условиях замкнуты, и размыкание их происходит при действии АГП. Образующаяся при этом дуга, как и раньше, разбивается в решетке на ряд коротких дуг. Пока горит дуга, цепь обмотки возбуждения остается замкнутой через якорь возбудителя.

При подходе тока к нулю часто наблюдается так называемый срыв тока, т. е. внезапное прекращение его. При большой индуктивности обмотки возбуждения синхронной

машины это сопровождается резким возраста­нием напряжения на обмотке. Для ограничения перена­пряжения дугогасящая решетка шунтирована относи­тельно большим сопротивлением r _ш.д, причем, чтобы дуга гасла по частям, а не вся сразу, решетка разбита на секции, которые присоединены к промежуточным ответвлениям этого сопротивления.

Из приведенных способов включения дугогасящей решетки предпочтительным является второй. Его пре­имуществом является относительная простота выполне­ния (меньше контактов), большая надежность, отсутст­вие дополнительного сопротивления r‘. Помимо того, если при параллельном включении решетки напряже­ние на обмотке возбуждения практически равно напря­жению на решетке при горении в ней дуги, то при по­следовательном включении это напряжение меньше на­пряжения на решетке на величину напряжения возбудителя. Поэтому в дальнейшем рассматриваем только последовательное включение дугогасящей ре­шетки.

Считая напряжение возбудителя u_в (практически равное предшествующему напряжению на кольцах ро­тора u_j0) неизменным, для цепи возбуждения в схеме рис. 8-7,6 при гашении поля имеем:

где u_д=30n—напряжение на решетке (из n пластин)

при горении дуги, в.

Интегрирование этого уравнения приводит к выра­жению для тока:

(8-29)

Напряжение на дугогасящей решетке . u_д = (1+k)u_f0, (8-30)

поэтому выражение (8-29) можно представить в иной форме:

Из структуры (8-29) непосредственно следует, что включение дугогасящей решетки эквивалентно внезапно­му включению в цепь обмотки возбуждения постоянной э. д. с., равной u_д и направленной против u_в. При этом нужно иметь в виду, что (8-29) и (8-31) справедливы лишь в течение времени горения дуги, которое при от­сутствии демпферных обмоток является также временем

if.Uf,us

Рис. 8-8. Гашение поля с помощью дугогасительной решетки, включенной последовательно с об­моткой возбуждения.

гашения поля t_гаш. Это время легко найти из (8-31) при i_f = 0:

(8-32)

при котором соблюдается то же значе­ние U_fm.

Кривая изменения тока i_f заканчивается при пересе­чении с осью абсцисс, т. е. при t_гаш==t_д; пунктиром по­казано ее продолжение, соответствующее (8-29) или (8-31). Напряжение на дугогасящей решетке при горении дуги постоянно и равно (l+k)u_fo=6u_fo; после погасания дуги оно падает до напряжения возбудителя. Напряже­ние на обмотке возбуждения при возникновении дуги, меняя знак, увеличивается до ku_f0=5u_fo и при погаса­нии ее падает до нуля.

Теперь рассмотрим, как сказывается наличие демп­ферных обмоток на процессе гашения поля. Для этой цели снова обратимся к результатам, полученным в гл. 4.

Поперечная демпферная обмотка не имеет магнитной связи с обмотками в продольной оси ротора, поэтому не оказывает влияния на процесс гашения поля.

Наличие продольной демпферной обмотки прежде всего скажется в том, что затухание потока Ф_d и обу­словленной им э. д. с. статора будет происходить с боль­шей постоянной времени; в соответствии с (4-24) посто­янная времени практически равна сумме постоянных времени продольной демпферной обмотки и обмотки воз­буждения с учетом введенного в нее разрядного сопро­тивления, т. е.

и время гашения согласно (8-26)

т. е. оно больше, чем при отсутствии продольной демп­ферной обмотки, что является, конечно, нежелательным.

С другой стороны, продольная демпферная обмотка в процессе гашения принимает на себя часть энергии магнитного поля ротора, чем облегчает условия для об­мотки возбуждения и включенного в ее цепь автомата гашения поля.

Используя приближенное соотношение (4-26), легко найти, что при σ=0 ток в обмотке возбуждения мгновенно падает до

а затем затухает по экспоненте с постоянной времени Т_гаш, опре­деляемой по (8-33). В продольной демпферной обмотке, напротив, ток мгновенно возрастает; его начальное значение, приведенное к обмотке возбуждения, будет:

(8-36)

а далее затухает с той же закономерностью.

В действительности σ>0 и соответственно T»_d>0, поэтому вне­запных изменений токов не происходит. Они сглаживаются быстро-затухающими токами i»_f и i»_id—

(8-39) Время горения дуги [из (8-37) при i_t = 0] ; (8-40)

при значениях k, близких к значению отношения Т_fo/Т_1do, более точ­ным является выражение:

Время гашения поля

Изменение магнитного потока Ф_d на первой стадии гашения определяется изменением н. с. ротора, т. е. суммы приведенных то­ков обмотки возбуждения и продольной демпферной обмотки, что приводит к выражению

а на второй стадии — изменением только тока продольной демп­ферной обмотки, т. е.

, (8-43)

где Ф_d02 — поток в начале второй стадии.

На рис. 8-9,6 приведены кривые изменения отдельных величин при гашении поля дугогасящей решеткой. Они построены при тех же исходных условиях, что и кривые рис. 8-8, но добавлена лишь продольная демпферная обмотка с указанными выше пара­метрами. Сравнение показывает, что, хотя время горения дуги сократилось, время гашения поля возросло почти в 2,5 раза. Из это­го примера наглядно видно, что демпферные обмотки существенно снижают эффективность гашения поля дугогасящей решеткой и, естественно, тем сильнее, чем больше постоянная времени 7_1do. Поэтому у турбогенераторов это сказывается гораздо сильнее, чем у гидрогенераторов.

Поскольку поперечная демпферная обмотка не имеет магнитной связи с обмотками, расположенными в продольной оси ротора, она не оказывает влияния на процесс гашения поля.

До сих пор предполагалось, что гашение поля осуще­ствляется при работе синхронной машины на холостом ходу. Однако все полученные выводы и выражения лег­ко могут быть распространены на условия, когда цепь статора замкнута в общем случае через х_вн. Для этого достаточно всюду вместо постоянных времени T_fо и T_1do ввести их значения при замкнутой цепи статора T’_fи Т’_1d, определяемые по (7-45) и (7-48), где x_вн входит в состав x_d. и x’_d.

Вследствие того, что постоянные времени обмоток ро­тора при замкнутой цепи статора меньше, процесс га­шения поля в этих условиях протекает быстрее.

Если гашение поля происходит в условиях короткого замыкания или иного переходного процесса, предшест­вующий ток в обмотках ротора может состоять не толь­ко из вынужденной, но также и из свободных слагающих. 188

Это может привести к большим величинам напря­жения на обмотке возбуждения при гашении поля.

При ионном или тиристорном возбуждении гашение поля осуществляют путем перевода выпрямительной установки в инверторный режим. При этом условия га­шения поля могут быть созданы близкими к оптималь­ным.

u – напряжение статора

Рис. 8-10. Осциллограммы гашения поля.

а — генератора 4,5 Мва, разряд на постоянное активное сопротивление: б—то же разряд на дугогасящую решетку; в — гидрогенератора 105 Мвт, разряд на дугогасящую решетку при коротком замыкании и предшествующей работе с номинальным возбуждением; г — то же при холостом ходе.

Для иллюстрации процессов гашения поля на рис. 8-10 приведено несколько характерных осцилло­грамм этих процессов у различных генераторов. Обра­щает на себя внимание то, что при гашении решеткой, а также инвертированием выпрямительной установки ха­рактер изменения тока i_f очень близок к прямолинейно­му, соответствующему оптимальным условиям гашения. Продолжительность вхождения дуги в решетку, как вид­но, составляет сотые доли секунды.

Пример 8-3. Для турбогенератора типа ТВ2-100-2 известны сле­дующие параметры: 100 Мвт, 13,8 кв, x_σ=0,11; х»_d=0,138;

r_f=0,415 ом (при горячем состоянии обмотки); ток возбуждения при холостом ходе 270 а, то же при номинальной нагрузке 650 а; ис­пытательное напряжение обмотки возбуждения 3 200 в.

Определим время гашения поля этого турбогенератора при ис­пользовании: а) постоянного разрядного сопротивления и б) дугогасящей решетки.

Решение выполним для условий, когда статор замкнут накоротко и возбуждение имеет двукратную форсировку (относительно но­минального режима).

а) Гашение на разрядное сопротивление

Напряжение на обмотке возбуждения в предшествующем ре­жиме u_fо=0,415(2·650)=540 в. Допустимое напряжение согласно (8-21) U_доп=0,7·3200=2 240 в. Необходимое разрядное сопротив­ление из (8-24)

Постоянные времени при короткозамкнутом статоре:

(здесь x_аd = 1,8 – 0,11 =1,69).

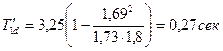
По (8-33) постоянная времени гашения поля

Т_гаш=0,27+ 1,1/ (4,15+1) = 0,48 сек

Ток возбуждения, при котором гаснет дуга переменного тока,

Следовательно, N= (2·650) /3=434 и время гашения по (8-34)

б) Гашение на дугогасящую решетку

Допустимое напряжение на решетке:

Необходимое число пластин в решетке п = 2780/30 = 93.

Принимаем к установке два автомата АГП-12, каждый из ко­торых имеет 40 пластин. При их последовательном соединении число

пластин составляет 2·40=80; тогда напряжение на решетке u_д=30·80=2400в и k=(2 400— 540) /’540 =3,4. Постоянные времени гашения:

при горении дуги Т_гаш1≈0,27+1,1 =1,37 сек;

после ее погасания Т_гаш2=0,27 сек.

Время горения дуги определяем по (8-40а), учитывая, что ста­тор короткозамкнут:

время гашения поля находим по (8-41), учитывая, что статор ко­роткозамкнут:

t_гаш =0,013 +0,27 In (325·3,4·0,27/1,1)= 1,53 сек.

Рекомендуется читателю самостоятельно провести аналогичный подсчет при условии, что генератор предварительно работал на хо­лостом ходу с номинальным напряжением.

Глава девятая

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник