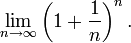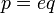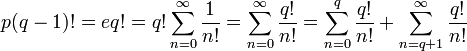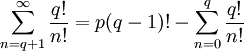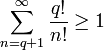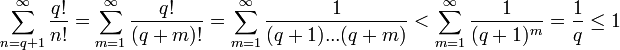Что измеряется в неперах
Непер
Непер выражает отношение одноимённых силовых величин (величин поля, как принято в международных документах), таких как электрическое напряжение или сила электрического тока, квадрат которых пропорционален мощности, в виде натурального логарифма этого отношения. Отношение энергетических величин — мощностей, выраженное в неперах, равняется одной второй натурального логарифма отношения этих мощностей.
Непер (1 Нп) соответствует значению e отношения силовых величин и значению e2 отношения энергетических величин.
Непер относится к единицам, не входящим в Международную систему единиц (СИ), но в соответствии с решением Международного комитета мер и весов допускается к применению без ограничений совместно с единицами СИ. В основном применяется в электросвязи, но постепенно вытесняется получившей широкое распространение единицей децибел.
Связанные понятия
Электри́ческий адмитта́нс (фр. admittance от лат. admittere пропускать, впускать) — комплексная проводимость двухполюсника для гармонического сигнала. В русскоязычной литературе этот термин обычно не применяется — вместо него употребляется термин «комплексная проводимость» (см., например, (Бессонов 1978)).
В статистике метод оценки с помощью апостериорного максимума (MAP) тесно связан с методом максимального правдоподобия (ML), но дополнительно при оптимизации использует априорное распределение величины, которую оценивает.
Модели дискретного выбора — экономические (эконометрические) модели, позволяющие описывать, объяснять и прогнозировать выбор между, двумя или более альтернативами (то есть когда множество альтернатив не более чем счетно). Модели дискретного выбора позволяют на основе некоторых характеристик (атрибутов) экономического субъекта или ситуации оценить вероятность выбора той или иной альтернативы.
Эквипотенциальные поверхности — понятие, применимое к любому потенциальному векторному полю, например, к статическому электрическому полю или к ньютоновскому гравитационному полю. Эквипотенциальная поверхность — это поверхность, на которой скалярный потенциал данного потенциального поля принимает постоянное значение (поверхность уровня потенциала). Другое, эквивалентное, определение — поверхность, в любой своей точке ортогональная силовым линиям поля.
Непер
Не́пер — безразмерная единица измерения отношения двух величин. Непер не входит в систему единиц СИ, однако, по решению Генеральной конференции по мерам и весам, допускается его применение без ограничений совместно с СИ. Единица названа в честь Джона Непера, который ввёл в математику понятие логарифма. Русское обозначение — Нп; международное — Np.
Так же, как бел и децибел, непер является единицей логарифмической шкалы. Разница между ними в том, что отношение величин, выраженное в белах (децибелах), предполагает использование десятичных логарифмов, тогда как для отношения в неперах используются натуральные логарифмы. Отношение величин x1 и x2 в неперах:
Неперы можно выразить через децибелы и наоборот:

Смотреть что такое «Непер» в других словарях:
НЕПЕР — единица логарифмической относительной величины (натурального логарифма отношения двух одноименных физических величин); названа в честь Дж. Непера. 1H =ln(F2/F1) при F2/F1=e 2,718, где F2 и F1 значения физических величин (напряжения, силы тока и… … Большой Энциклопедический словарь
НЕПЕР — (Napier) Джон (1550 1617), шотландский математик. Создал «кости Непера», счетное устройство, которое применил в изобретении ЛОГАРИФМОВ (1614), и современную систему обозначения арабскими цифрами … Научно-технический энциклопедический словарь
НЕПЕР — (Нп, Np), единица логарифмич. относит. величины (натурального логарифма отношения двух одноимённых физ. величин). Названа в честь шотл. математика Дж. Непера (J. Napier). 1Нп=ln?F2/F1? при F2/F1=e»2,718, где F2 и F1 значения напряжения, силы тока … Физическая энциклопедия
непер — сущ., кол во синонимов: 10 • единица (830) • невезение (26) • невезуха (11) • … Словарь синонимов
непер — НЕПЕР, а, НЕПЁР, а, м. Невезение, неудачное стечение обстоятельств. Пошёл непёр. От «пёр» везение, удача … Словарь русского арго
непер — Единица измерения отношения величин B1 и В2, выраженная через натуральный логарифм их отношения. Отношения А1/A2 амплитуд в неперах представляют в виде ln(A1/A2), отношения W1/W2 интенсивностей 0,5 ln(W1/W2). 1Нп=8,686 дБ. [Система неразрушающего … Справочник технического переводчика
Непер Д. — Джон Непер Джон Непер (англ. John Napier; 1550 1617) шотландский барон, математик, один из изобретателей логарифмов, первый публикатор логарифмических таблиц. Содержание 1 … Википедия
непер — единица логарифмической относительной величины (натурального логарифма отношения двух одноимённых физических величин); названа по имени Дж. Непера. 1 непер = ln(F2/F1) при F2/F1 = е≈2,718, где F2 и F1 значения физических величин (напряжения,… … Энциклопедический словарь
непер — (по шкотскиот математичар Џон Непер, 1550 1617) физ. единица за мерење на акустични и електрични вибрации; 1 непер = 8. 686 децибели … Macedonian dictionary
непер — (по имени шотл. ученого Дж. Непера (Napier), 1550 1617) единица логарифмической относительной величины; число в. выражается натуральным логарифмом отношения двух одноименных физических величин, напр, электрических токов, напряжений, мощностей; 1… … Словарь иностранных слов русского языка
Что такое децибел
Очень часто новички сталкивается с таким понятием, как децибел. Многие из них интуитивно догадываются, что это такое, но у большинства до сих пор возникают вопросы.
Что такое децибел?
Относительные логарифмические единицы Белы (децибелы) широко используются при количественных оценках параметров различных аудио, видео, измерительных устройств. Физическая природа сравниваемых мощностей может быть любой — электрической, электромагнитной, акустической, механической, — важно лишь, чтобы обе величины были выражены в одинаковых единицах — ваттах, милливаттах и т. п. Бел выражает отношение двух значений энергетической величины десятичным логарифмом этого отношения, причем под энергетическими величинами понимаются: мощность, энергия.
Кстати, эта единица получила свое название в честь Александра Белл (1847 — 1922) — американского ученого шотландского происхождения, основоположника телефонии, основателя всемирно известных компаний AT&T и «Bell Laboratories». Еще интересно напомнить, что во многих современных мобильных телефонах (смартфонах) обязательно есть выбираемый звук звонка (оповещения), так и называемый «bell». Впрочем, Бел относится к единицам, не входящим в Международную систему единиц (СИ), но в соответствии с решением Международного комитета мер и весов допускается к применению без ограничений совместно с единицами СИ. В основном применяется в электросвязи, акустике, радиотехнике.
Формулы для вычисления децибелов
P1 — мощность до усиления, Вт
P2 — мощность после усиления или ослабления, Вт
На практике, оказалось, что удобнее пользоваться уменьшенным в 10 раз значением Бел, т.е. децибел, поэтому:
дециБел (дБ) = 10 * lg(P2/P1)
Усиление или ослабление мощности в децибелах выражается формулой:
NдБ — усиление, либо ослабление мощности в децибелах
P1 — мощность до усиления, Вт
P2 — мощность после усиления или ослабления, Вт
Значения Бел, децибел могут быть со знаком «плюс», если P2 > P1 (усиление сигнала) и со знаком «минус», если P2
Во многих случаях, сравнение сигналов путем измерения мощностей может быть неудобным или невозможным — проще измерить напряжение или ток.
В этом случае, если мы сравниваем напряжения или токи, формула примет уже другой вид:
NдБ — усиление, либо ослабление мощности в децибелах
U1 — это напряжение до усиления, В
U2 — напряжение после усиления, В
I2 — сила тока после усиления, А
Вот небольшая табличка, в которой приведены основные отношения напряжений и соответствующее число децибел:
Дело в том, что операции умножения и деления над числами в обычном базисе, заменяются операциями сложения и вычитания в логарифмическом базисе. Например, у нас есть два каскадно-включенных усилителя с коэффициентами усиления K1 = 963 и K2 = 48. Какой общий коэффициент усиления? Правильно — он равен произведению K = K1 * K2. Вы можете в уме быстро вычислить 963*48? Я — нет. Я могу прикинуть K = 1000*50 = 50 тыс., не более. А, если нам известно, что K1 = 59 дБ и K2 = 33 дБ, то К = 59+33 = 92 дБ — сложить было не трудно, надеюсь.
Закон Вебера-Фехнера
Почему именно децибелы? Все исходит от закона Вебера-Фехнера, который говорит нам, что интенсивность ощущения человеческих чувств прямо-пропорциональна логарифму интенсивности какого-либо раздражителя.
Так светильник, в котором восемь лампочек, кажется нам настолько же ярче светильника из четырёх лампочек, насколько светильник из четырёх лампочек ярче светильника из двух лампочек. То есть количество лампочек должно увеличиваться каждый раз вдвое, чтобы нам казалось, что прирост яркости постоянен. То есть если добавить к нашим 32 лампочкам на графике еще одну лампочку, то мы даже и не заметим разницы. Для того, чтобы для нашего глаза была заметна разница, мы должны к 32 лампочкам добавить еще 32 лампочки, и т.д. Или иными словами, для того, чтобы нам казалось, что наш светильник плавно набирает яркость, нам надо зажигать вдвое больше лампочек каждый раз, чем было предыдущее значение.
Поэтому децибел действительно удобнее в некоторых случаях, так как сравнивать две величины намного проще в маленьких цифрах, чем в миллионах и миллиардах. А так как электроника — это чисто физическое явление, то и децибелы не обошли ее стороной.
Децибелы и АЧХ усилителя
Как вы помните в прошлом примере с ОУ, у нас неинвертирующий усилитель усиливал сигнал в 10 раз. Если посмотреть в нашу табличку, то это получается 20 дБ относительно входного сигнала. Ну да, так оно и есть:
Также в дБ на некоторых графиках АЧХ обозначают наклон характеристики АЧХ. Это может выглядеть примерно вот так:
Давайте рассмотрим пример. Имеем фильтр высоких частот (ФВЧ) первого порядка, собранного на RC-цепи.
Его АЧХ будет выглядеть следующим образом (кликните для полного открытия)
Итак возьмем первую точку на частоте в 10 Герц. На частоте в 10 Герц амплитуда сигнала уменьшилась на 44 дБ, это видно в правом нижнем углу (out:-44)
Умножаем частоту на 10 (декада) и получаем вторую точку в 100 Герц. На частоте в 100 Герц наш сигнал уменьшился приблизительно на 24 дБ
Что еще измеряют в децибелах?
Uc — это эффективное значение напряжения сигнала, В
Uш — эффективное значение напряжения шума, В
Чем выше значение сигнал/шум, тем более чистый звук обеспечивается аудиосистемой. Для музыкальной аппаратуры желательно, чтобы это отношение было не менее 75 дБ, а для Hi-Fi аппаратуры не менее 90 дБ. Не имеет значение физическая природа сигнала, важно, чтобы единицы были в одинаковых измерениях.
В качестве единицы логарифмического отношения двух одноимённых физических величин применяется также непер (Нп) — 1 Нп
0,8686 Б. В основе лежит не десятичный (lg), а натуральный (ln) логарифм отношений. В настоящее время используется редко.
Во многих случаях, удобно сравнивать между собой не произвольные величины, а одну величину относительно другой, названной условно опорной (нулевой, базовой).
В электротехнике, в качестве такой опорной или нулевой величины выбрано значение мощности равное 1 мВт выделяемое на резисторе сопротивлением 600 Ом.
В этом случае, базовыми значениями при сравнении напряжений или токов станут величины 0.775 В или 1.29 мА.
Для звуковой мощности такой базовой величиной является 20 микроПаскаль (0 дБ), а порог +130 дБ считается болевым для человека:
Более подробно об этом написано в Википедии по этой ссылке.
Для случаев когда в качестве базовых значений используются те или иные конкретные величины, придуманы даже специальные обозначения единиц измерений:
dbW (дБВт) — здесь отсчет идет относительно 1 Ватта (Вт). Например, пусть уровень мощности составил +20 дБВт. Это значит что мощность увеличилась в 100 раз, то есть на 100 Вт.
dBm (дБм) — здесь у нас отсчет уже идет относительно 1 милливатта (мВт). Например, уровень мощности в +30дБм будет соответственно равен 1 Вт. Не забываем, что это у нас энергетические децибелы, поэтому для них будет справедлива формула
Следующие характеристики — это уже амплитудные децибелы. Для них будет справедлива формула
dBV (дБВ) — как вы догадались, опорное напряжение 1 Вольт. Например, +20дБВ даст — это 10 Вольт
От дБВ также вытекают другие виды децибелов с разными приставками:
dBmV (дБмВ) — опорный уровень 1 милливольт.
dBuV (дБмкВ) — опорное напряжение 1 микровольт.
Здесь я привел наиболее употребимые специальные виды децибелов в электронике.
Децибелы используются и в других отраслях, где они также показывают отношение каких-либо двух измеряемых величин в логарифмическом масштабе.
Также на YouTube есть интересное видео о децибелах.
Джон Непер
Джон Непер (1550—1617) — шотландский барон (8-й лэрд Мерчистона), математик, один из изобретателей логарифмов, первый публикатор логарифмических таблиц.
Биография
Мерчистон, родовой замок Непера
В ранней молодости, тотчас же по окончании курса в Сент-Эндрюсском университете, куда он поступил в 1563 году, Непер совершил путешествие по Германии, Франции и Италии, из которого вернулся на родину в 1571 году. Поселившись в своем родном замке и женившись в том же году, он затем уже никогда не оставлял Шотландии.
Всё его время было посвящено занятиям богословскими предметами и математикой. По его собственным словам, истолкование пророчеств всегда составляло главный предмет его занятий, математика же служила для него только отдыхом.
Тем не менее Непер вошёл в историю как изобретатель замечательного вычислительного инструмента — таблицы логарифмов. Это открытие вызвало гигантское облегчение труда вычислителя.
Лаплас говорил, что Непер своим изобретением «продлил жизнь астрономов», упростив их вычисления.
В честь Джона Непера названы: кратер на Луне; астероид 7096 Непер (1992 год); логарифмическая безразмерная единица, измеряющая отношение двух величин; университет в Эдинбурге (Edinburgh Napier University).
Открытие логарифмов
Потребность в сложных расчётах в XVI веке быстро росла. Значительная часть трудностей была связана с умножением и делением многозначных чисел. В ходе тригонометрических расчётов, Неперу пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание.
В 1614 году Непер опубликовал в Эдинбурге сочинение под названием «Описание удивительной таблицы логарифмов», на латинском языке (56 страниц текста и 90 страниц таблиц). Там было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1′.
Сочинение разделено на 2 книги, из которых первая посвящена логарифмам, а вторая — плоской и сферической тригонометрии, причём вторая часть одновременно служит практическим пособием по первой. Более развёрнутое описание содержалось в другом труде, изданном посмертно его сыном; там же Непер пояснил, как он составлял свои таблицы.
Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую. Однако правила логарифмирования для неперовой функции отличались от правил для современного логарифма.
Все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.
В 1615 году Непера посетил оксфордский профессор математики Генри Бригс. Непер уже был болен, поэтому не смог усовершенствовать свои таблицы, однако дал Бригсу рекомендации видоизменить определение логарифма, приблизив его к современному. Бригс опубликовал свои таблицы в год смерти Непера (1617). Они уже включали десятичные, а не натуральные, логарифмы, и не только синусов, но и самих чисел (от 1 до 1000, с 14 знаками). Логарифм единицы теперь, как положено, был равен нулю.
Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Вега появилось только в 1857 году в Берлине (таблицы Бремивера).
В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.
Современное определение логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.
Немалую популярность получил придуманный Непером оригинальный прибор для быстрого умножения (палочки Непера).
Применение и развитие теория логарифмов нашла в рекурсивных алгоритмах, теории фракталов, в теории чисел и математическом анализе, в статистике и теории вероятностей, информатике и вычислительной технике, механике и физике, химии, теории музыки, психологии и философии.
Неперово число
Играет важную роль в дифференциальном и интегральном исчислении, а также многих других разделах математики.

Содержание
Способы определения
Число e может быть определено несколькими способами.
Свойства
История
Данное число иногда называют неперовым в честь шотландского учёного Непера, автора работы «Описание удивительной таблицы логарифмов» (1614 год). Однако это название не совсем корректно, так как у него логарифм числа x был равен 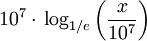
Впервые константа негласно присутствует в приложении к переводу на английский язык вышеупомянутой работы Непера, опубликованному в 1618 году. Негласно, потому что там содержится только таблица натуральных логарифмов, определённых из кинематических соображений, сама же константа не присутствует (см.: Непер).
Предполагается, что автором таблицы был английский математик Отред.
Саму же константу впервые вычислил швейцарский математик Бернулли при анализе следующего предела:
Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Лейбница Гюйгенсу, 1690—1691 годы.
Букву e начал использовать Эйлер в 1727 году, а первой публикацией с этой буквой была его работа «Механика, или Наука о движении, изложенная аналитически» 1736 год. Соответственно, e обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву c, буква e применялась чаще и в наши дни является стандартным обозначением.
Почему была выбрана именно буква e, точно неизвестно. Возможно, это связано с тем, что с неё начинается слово exponential («показательный», «экспоненциальный»). Другое предположение заключается в том, что буквы a, b, c и d уже довольно широко использовались в иных целях, и e была первой «свободной» буквой. Неправдоподобно предположение, что Эйлер выбрал e как первую букву в своей фамилии (нем. Euler ).
Способы запоминания
Доказательство иррациональности
Пускай 
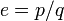
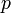
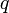
Умножая обе части уравнения на 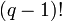
Переносим 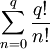
Все слагаемые правой части целые, следовательно:
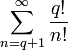
Но с другой стороны