Что измеряется для оценки вычислительной сложности алгоритма
Оценка сложности алгоритмов, или Что такое О(log n)
Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы хотите стать хорошим программистом, но так и не понимаете, что это значит, — данная статья для вас.
Оценка сложности
Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.
Примеры
O(n) — линейная сложность
Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.
O(log n) — логарифмическая сложность
Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.
O(n 2 ) — квадратичная сложность
Бывают и другие оценки по сложности, но все они основаны на том же принципе.
Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.
Наглядно
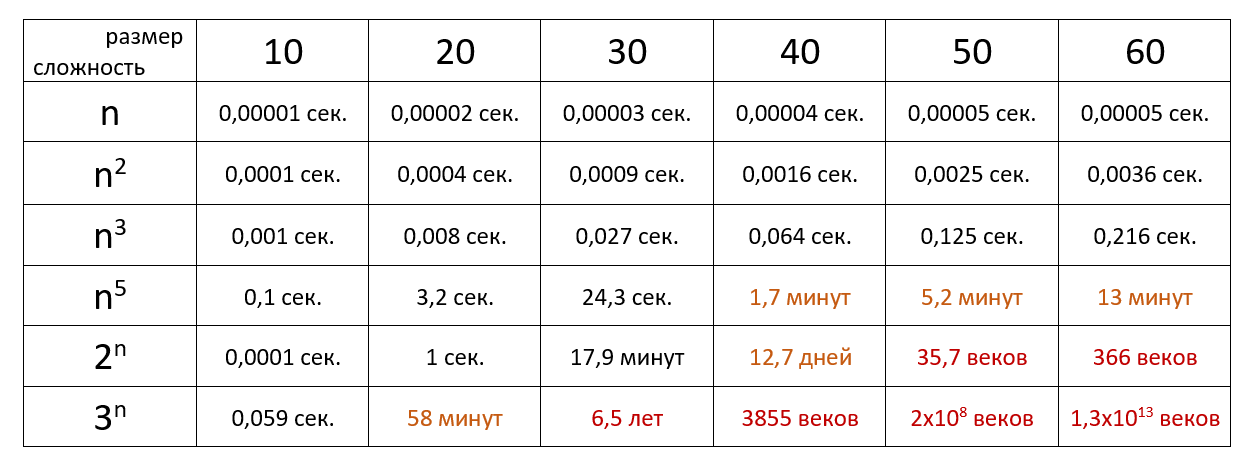
Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 10 6 операций в секунду:
Если хочется подробнее и сложнее, заглядывайте в нашу статью из серии «Алгоритмы и структуры данных для начинающих».
Вычислительная сложность
Из Википедии — свободной энциклопедии
Вычисли́тельная сло́жность — понятие в информатике и теории алгоритмов, обозначающее функцию зависимости объёма работы, которая выполняется некоторым алгоритмом, от размера входных данных. Раздел, изучающий вычислительную сложность, называется теорией сложности вычислений. Объём работы обычно измеряется абстрактными понятиями времени и пространства, называемыми вычислительными ресурсами. Время определяется количеством элементарных шагов, необходимых для решения задачи, тогда как пространство определяется объёмом памяти или места на носителе данных. Таким образом, в этой области предпринимается попытка ответить на центральный вопрос разработки алгоритмов: «как изменится время исполнения и объём занятой памяти в зависимости от размера входа?». Здесь под размером входа понимается длина описания данных задачи в битах (например, в задаче коммивояжёра длина входа почти пропорциональна количеству городов и дорог между ними), а под размером выхода — длина описания решения задачи (наилучшего маршрута в задаче коммивояжёра).
С теоретической информатикой тесно связаны такие области как анализ алгоритмов и теория вычислимости. Связующим звеном между теоретической информатикой и алгоритмическим анализом является тот факт, что их формирование посвящено анализу необходимого количества ресурсов определённых алгоритмов решения задач, тогда как более общим вопросом является возможность использования алгоритмов для подобных задач. Конкретизируясь, попытаемся классифицировать проблемы, которые могут или не могут быть решены при помощи ограниченных ресурсов. Сильное ограничение доступных ресурсов отличает теорию вычислительной сложности от вычислительной теории, последняя отвечает на вопрос какие задачи, в принципе, могут быть решены алгоритмически.
Анализ сложности алгоритмов. Примеры
Алгоритм — это точное предписание, однозначно определяющее вычислительный процесс, ведущий от варьируемых начальных данных к искомому результату [1].
При разработке алгоритмов очень важно иметь возможность оценить ресурсы, необходимые для проведения вычислений, результатом оценки является функция сложности (трудоемкости). Оцениваемым ресурсом чаще всего является процессорное время (вычислительная сложность) и память (сложность алгоритма по памяти). Оценка позволяет предсказать время выполнения и сравнивать эффективность алгоритмов.
Содержание:
Модель RAM (Random Access Machine)
Каждое вычислительное устройство имеет свои особенности, которые могут влиять на длительность вычисления. Обычно при разработке алгоритма не берутся во внимание такие детали, как размер кэша процессора или тип многозадачности, реализуемый операционной системой. Анализ алгоритмов проводят на модели абстрактного вычислителя, называемого машиной с произвольным доступом к памяти (RAM).
Модель состоит из памяти и процессора, которые работают следующим образом:
Несмотря на то, что такая модель далека от реального компьютера, она замечательно подходит для анализа алгоритмов. После того, как алгоритм будет реализован для конкретной ЭВМ, вы можете заняться профилированием и низкоуровневой оптимизацией, но это будет уже оптимизация кода, а не алгоритма.
Подсчет операций. Классы входных данных
Одним из способов оценки трудоемкости (\(T_n\)) является подсчет количества выполняемых операций. Рассмотрим в качестве примера алгоритм поиска минимального элемента массива.
При выполнении этого алгоритма будет выполнена:
Точное количество операций будет зависеть от обрабатываемых данных, поэтому имеет смысл говорить о наилучшем, наихудшем и среднем случаях. При этом худшему случаю всегда уделяется особое внимание, в том числе потому, что «плохие» данные могут быть намеренно поданы на вход злоумышленником.
Понятие среднего случая используется для оценки поведения алгоритма с расчетом на то, что наборы данных равновероятны. Однако, такая оценка достаточно сложна:
Асимптотические обозначения
Подсчет количества операций позволяет сравнить эффективность алгоритмов. Однако, аналогичный результат можно получить более простым путем. Анализ проводят с расчетом на достаточно большой объем обрабатываемых данных (\( n \to \infty \)), поэтому ключевое значение имеет скорость роста функции сложности, а не точное количество операций.
При анализе скорости роста игнорируются постоянные члены и множители в выражении, т.е. функции \(f_x = 10 \cdot x^2 + 20 \) и \( g_x = x^2\) эквивалентны с точки зрения скорости роста. Незначащие члены лишь добавляют «волнистости», которая затрудняет анализ.
В оценке алгоритмов используются специальные асимптотические обозначения, задающие следующие классы функций:
Запись \(f_n = \mathcal
Ограниченность функции g снизу функцией f записывается следующим образом: \(g_n =\Omega(f_n)\). Нотации \(\Omega\) и \(\mathcal

Если функции f и g имеют одинаковую скорость роста (\(f_n = \Theta(g_n)\)), то существуют положительные константы \(c_1\) и \(c_2\) такие, что \(\exists n_0 > 0 : \forall n > n_0, f_n \leq c_1 \cdot g_n, f_n \geq c_2 \cdot g_n\). При этом \(f_n = \Theta(g_n) \Leftrightarrow g_n = \Theta(f_n)\).

Примеры анализа алгоритмов
Алгоритм поиска минимального элемента массива, приведенный выше, выполнит N итераций цикла. Трудоемкость каждой итерации не зависит от количества элементов массива, поэтому имеет сложность \(T^
Алгоритм пузырьковой сортировки (bubble sort) использует два вложенных цикла. Во внутреннем последовательно сравниваются пары элементов и если оказывается, что элементы стоят в неправильном порядке — выполняется перестановка. Внешний цикл выполняется до тех пор, пока в массиве найдется хоть одна пара элементов, нарушающих требуемый порядок [2].
Трудоемкость функции swap не зависит от количества элементов в массиве, поэтому оценивается как \(T^
В алгоритме сортировки выбором массив мысленно разделяется на упорядоченную и необработанную части. На каждом шаге из неупорядоченной части массива выбирается минимальный элемент и добавляется в отсортированную часть [2].
Для поиска наименьшего элемента неупорядоченной части массива используется функция indMin, принимающая массив, размер массива и номер позиции, начиная с которой нужно производить поиск. Анализ сложности этой функции можно выполнить аналогично тому, как это сделано для функции min — количество операций линейно зависит от количества обрабатываемых элементов: \( T^
У сортировки выбором нет ветвлений, которые могут внести различия в оценку наилучшего и наихудшего случаев, ее трудоемкость: \(T^
Математический аппарат анализа алгоритмов
Выше были рассмотрены асимптотические обозначения, используемые при анализе скорости роста. Они позволяют существенно упростить задачу отбросив значительную часть выражения. Однако, в математическом анализе имеется целый ворох таких приемов.
Формулы суммирования
В примерах, рассмотренных выше, мы уже сталкивались с нетривиальными формулами суммирования. Чтобы дать оценку суммы можно использовать ряд известных тождеств:
Первые из этих тождеств достаточно просты, их можно вывести используя метод математической индукции. Если под знаком суммы стоит более сложная формула, как в двух последних тождествах — суммирование можно заменить интегрированием (взять интеграл функции гораздо проще, ведь для этого существует широкий спектр приемов).
Суммирование и интегрирование
Известно, что интеграл можно понимать как площадь фигуры, размещенной под графиком функции. Существует ряд методов аппроксимации (приближенного вычисления) интеграла, к ним относится, в частности, метод прямоугольников. Площадь под графиком делится на множество прямоугольников и приближенно вычисляется как сумма их площадей. Следовательно, возможен переход от интеграла к сумме и наоборот.
аппроксимация интеграла левыми прямоугольниками
аппроксимация интеграла правыми прямоугольниками
На рисунках приведен пример аппроксимации функции \(f_x = \log x\) левыми и правыми прямоугольниками. Очевидно, они дадут верхнюю и нижнюю оценку площади под графиком:
В частности, такой метод позволяет оценить алгоритмы, имеющие логарифмическую сложность (две последние формулы суммирования).
Сравнение сложности алгоритмов. Пределы
Сложность алгоритмов определяется для больших объемов обрабатываемых данных, т.е. при \(n\to\infty\). В связи с этим, при сравнении трудоемкости двух алгоритмов можно рассмотреть предел отношения функций их сложности: \(\lim\limits_
Если функции достаточно сложны, то такой прием значительно упрощает задачу, т.к. вместо предела отношения функций можно анализировать предел отношения их производных (согласно правилу Лопиталя): \(\lim\limits_
Допустим, требуется сравнить эффективность двух алгоритмов с оценками сложности \(\mathcal
Логарифмы и сложность алгоритмов. Пример
По определению \(\log_a
При анализе алгоритмов обычно встречаются логарифмы по основанию 2, однако основание не играет большой роли, поэтому зачастую не указывается. Последняя формула позволяет заменить основание логарифма, домножив его на константу, но константы отбрасываются при асимптотическом анализе.
Логарифмической сложностью обладают алгоритмы, для которых не требуется обрабатывать все исходные данные, они используют принцип «разделяй и властвуй». На каждом шаге часть данных (обычно половина) отбрасывается. Примером может быть функция поиска элемента в отсортированном массиве (двоичного поиска):
Очевидно, что на каждом шаге алгоритма количество рассматриваемых элементов сокращается в 2 раза. Количество элементов, среди которых может находиться искомый, на k-том шаге определяется формулой \(\frac
Результаты анализа. Замечания. Литература
Оценка сложности — замечательный способ не только сравнения алгоритмов, но и прогнозирования времени их работы. Никакие тесты производительности не дадут такой информации, т.к. зависят от особенностей конкретного компьютера и обрабатывают конкретные данные (не обязательно худший случай).
Анализ алгоритмов позволяет определить минимально возможную трудоемкость, например:
Нередко на собеседованиях просят разработать алгоритм с лучшей оценкой, чем возможно. Сами задачи при этом сводятся к какому-либо стандартному алгоритму. Человек, не знакомый с асимптотическим анализом начнет писать код, но требуется лишь обосновать невозможность существования такого алгоритма.
Оценка сложности алгоритмов
Введение
Для любого программиста важно знать основы теории алгоритмов, так как именно эта наука изучает общие характеристики алгоритмов и формальные модели их представления. Ещё с уроков информатики нас учат составлять блок-схемы, что, в последствии, помогает при написании более сложных задач, чем в школе. Также не секрет, что практически всегда существует несколько способов решения той или иной задачи: одни предполагают затратить много времени, другие ресурсов, а третьи помогают лишь приближённо найти решение.
Всегда следует искать оптимум в соответствии с поставленной задачей, в частности, при разработке алгоритмов решения класса задач.
Важно также оценивать, как будет вести себя алгоритм при начальных значениях разного объёма и количества, какие ресурсы ему потребуются и сколько времени уйдёт на вывод конечного результата.
Этим занимается раздел теории алгоритмов – теория асимптотического анализа алгоритмов.
Предлагаю в этой статье описать основные критерии оценки и привести пример оценки простейшего алгоритма. На Хабрахабре уже есть статья про методы оценки алгоритмов, но она ориентирована, в основном, на учащихся лицеев. Данную публикацию можно считать углублением той статьи.
Определения
Основным показателем сложности алгоритма является время, необходимое для решения задачи и объём требуемой памяти.
Также при анализе сложности для класса задач определяется некоторое число, характеризующее некоторый объём данных – размер входа.
Итак, можем сделать вывод, что сложность алгоритма – функция размера входа.
Сложность алгоритма может быть различной при одном и том же размере входа, но различных входных данных.
Существуют понятия сложности в худшем, среднем или лучшем случае. Обычно, оценивают сложность в худшем случае.
Временная сложность в худшем случае – функция размера входа, равная максимальному количеству операций, выполненных в ходе работы алгоритма при решении задачи данного размера.
Ёмкостная сложность в худшем случае – функция размера входа, равная максимальному количеству ячеек памяти, к которым было обращение при решении задач данного размера.
Порядок роста сложности алгоритмов
Порядок роста сложности (или аксиоматическая сложность) описывает приблизительное поведение функции сложности алгоритма при большом размере входа. Из этого следует, что при оценке временной сложности нет необходимости рассматривать элементарные операции, достаточно рассматривать шаги алгоритма.
Шаг алгоритма – совокупность последовательно-расположенных элементарных операций, время выполнения которых не зависит от размера входа, то есть ограничена сверху некоторой константой.
Виды асимптотических оценок
O – оценка для худшего случая
Рассмотрим сложность f(n) > 0, функцию того же порядка g(n) > 0, размер входа n > 0.
Если f(n) = O(g(n)) и существуют константы c > 0, n0 > 0, то
0 n0.
Функция g(n) в данном случае асимптотически-точная оценка f(n). Если f(n) – функция сложности алгоритма, то порядок сложности определяется как f(n) – O(g(n)).
Данное выражение определяет класс функций, которые растут не быстрее, чем g(n) с точностью до константного множителя.
Примеры асимптотических функций
| f(n) | g(n) |
|---|---|
| 2n 2 + 7n — 3 | n 2 |
| 98n*ln(n) | n*ln(n) |
| 5n + 2 | n |
| 8 | 1 |
Ω – оценка для лучшего случая
Критерии оценки сложности алгоритмов
Равномерный весовой критерий (РВК) предполагает, что каждый шаг алгоритма выполняется за одну единицу времени, а ячейка памяти за одну единицу объёма (с точностью до константы).
Логарифмический весовой критерий (ЛВК) учитывает размер операнда, который обрабатывается той или иной операцией и значения, хранимого в ячейке памяти.
Временная сложность при ЛВК определяется значением l(Op), где Op – величина операнда.
Ёмкостная сложность при ЛВК определяется значением l(M), где M – величина ячейки памяти.
Пример оценки сложности при вычислении факториала
Необходимо проанализировать сложность алгоритма вычисление факториала. Для этого напишем на псевдокоде языка С данную задачу:
Временная сложность при равномерном весовом критерии
Достаточно просто определить, что размер входа данной задачи – n.
Количество шагов – (n — 1).
Таким образом, временная сложность при РВК равна O(n).
Временная сложность при логарифмическом весовом критерии
В данном пункте следует выделить операции, которые необходимо оценить. Во-первых, это операции сравнения. Во-вторых, операции изменения переменных (сложение, умножение). Операции присваивания не учитываются, так как предполагается, что она происходят мгновенно.
Итак, в данной задаче выделяется три операции:
Сложность алгоритмов. Big O. Основы.
Развитие технологий привело к тому, что память перестала быть критическим ресурсом. Поэтому когда говорят об анализе сложности алгоритма, обычно подразумевают то, насколько быстро он работает.
Но ведь время выполнения алгоритма зависит от того, на каком устройстве его запустить. Один и тот же алгоритм запущенный на разных устройствах выполняется за разное время.
Big O показывает верхнюю границу зависимости между входными параметрами функции и количеством операций, которые выполнит процессор.
Распространённые сложности алгоритмов
Здесь рассмотрены именно распространённые виды, так как рассмотреть все варианты врядли возможно. Всё зависит от алгоритма, который вы оцениваете. Всегда может появится какая-то дополнительная переменная (не константа), которую необходимо будет учесть в функции Big O.
Означает, что вычислительная сложность алгоритма не зависит от входных данных. Однако, это не значит, что алгоритм выполняется за одну операцию или требует очень мало времени. Это означает, что время не зависит от входных данных.
Пример № 1.
У нас есть массив из 5 чисел и нам надо получить первый элемент.
Насколько возрастет количество операций при увеличении размера входных параметров?
Нинасколько. Даже если массив будет состоять из 100, 1000 или 10 000 элементов нам всеравно потребуется одна операция.
Пример № 2.
Сложение двух чисел. Функция всегда выполняет константное количество операций.
Пример № 3.
Размер массива. Опять же, функция всегда выполняет константной количество операций.
Означает, что сложность алгоритма линейно растёт с увеличением входных данных. Другими словами, удвоение размера входных данных удвоит и необходимое время для выполнения алгоритма.
Такие алгоритмы легко узнать по наличию цикла по каждому элементу массива.
Пример № 3.
Означает, что сложность алгоритма растёт логарифмически с увеличением входных данных. Другими словами это такой алгоритм, где на каждой итерации берётся половина элементов.
К алгоритмам с такой сложностью относятся алгоритмы типа “Разделяй и Властвуй” (Divide and Conquer), например бинарный поиск.
Означает, что удвоение размера входных данных увеличит время выполнения чуть более, чем вдвое.
Примеры алгоритмов с такой сложностью: Сортировка слиянием или множеством n элементов.
Означает, что удвоение размера входных данных увеличивает время выполнения в 4 раза. Например, при увеличении данных в 10 раз, количество операций (и время выполнения) увеличится примерно в 100 раз. Если алгоритм имеет квадратичную сложность, то это повод пересмотреть необходимость использования данного алгоритма. Но иногда этого не избежать.
Такие алгоритмы легко узнать по вложенным циклам.
Пример № 1.
В функции есть цикл в цикле, каждый из них проходит массив длиной n, следовательно сложность будет: O(n * n) = O(n 2 )
Зачем изучать Big O
Шпаргалка
Небольшие подсказки, которые помогут определить сложность алгоритма.