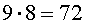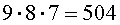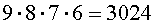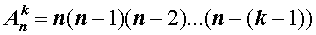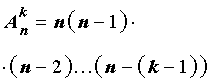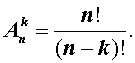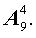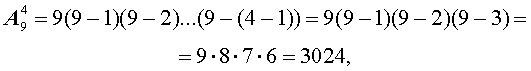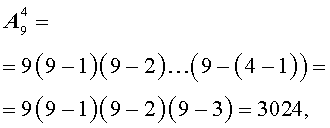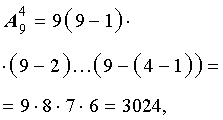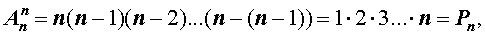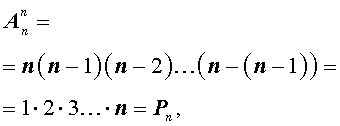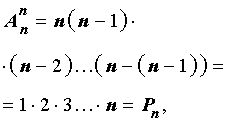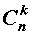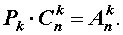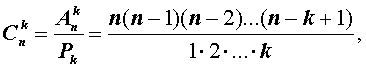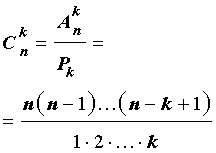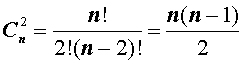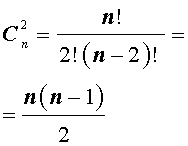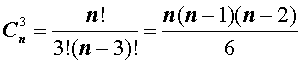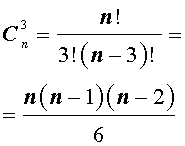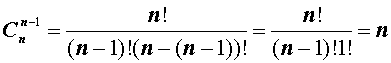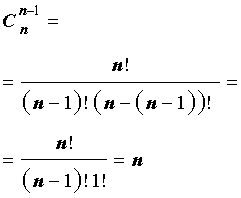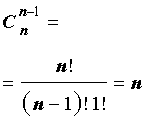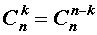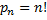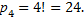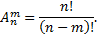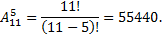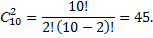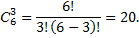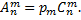Чем отличаются сочетания и размещения элементов

Сочетания и размещения — что это такое и в чем разница

Оба этих понятия – сочетание и размещение – относятся к науке комбинаторике. Это раздел математики, созданный учеными Б. Паскалем и П. Ферма в процессе исследования теории карточных игр. Комбинаторика используется в решении задач особенного рода: когда требуется вычислить количество потенциальных вариантов для какой-либо ситуации. Примером может служить подсчет возможных позиций на шахматной доске после первого хода «черных» и «белых».

О сочетании и размещении говорят, когда из множества необходимо выбрать какое-либо подмножество. Понятия эти весьма близки по своему смыслу, поэтому так трудно бывает понять разницу между ними. Но она существует (причем принципиальная!). Ниже об этом достаточно простым языком написано в статье.

Сочетания

Сочетание – это подмножество, состоящее из К элементов, выбранных из множества, включающего в себя N элементов. При этом выполняется такое условие: N > К.

Важный момент: порядок расположения в данной выборке никакого значение не имеет. То есть комбинации, отличающиеся порядком размещения элементов, но не составом, считаются одинаковыми сочетаниями.

Образно проиллюстрировать понятие можно на примере лотереи. Предположим, человеку предлагается угадать 3 выпавшие цифры из 15-ти. Он выбрал следующий набор – 1, 6, 10. И уже не важно, в каком порядке они выпадут: 1, 6, 10; 1, 10, 6; 10, 1, 6; 10, 6, 1; 6, 10, 1; 6, 1, 10. Главное – состав комбинации. Если он совпадает с загаданным накануне набором цифр, игрок считается победителем.

Сочетания обозначаются следующим образом: С К _N. Где N – количество элементов в множестве, а К – количество объектов в производимой выборке. Для нашего примера N = 15, а К = 3.

Существует формула для определения числа возможных сочетаний в множестве. Выглядит она так: N!/((N-K)!*K!) подставим цифры из нашего примера:

Это означает, что из 15 чисел можно составить 455 различных комбинаций, включающих в себя три разных числа.

Такие подсчеты в нашем примере позволяют определить велики ли шансы субъекта на выигрыш.

Размещения

В самом названии этого термина присутствует корень, позволяющий понять его суть. Размещение – тоже подмножество, выбранное из первоначального множества. Но здесь уже существенное значение имеет место расположения элемента в комбинации. То есть если сочетания могут различаться только составом объектов, то размещения разнятся и составом, и порядком следования элементов.

Получается, что количество размещений всегда превосходит число сочетаний, при условии выборки из одного и того же множества.

Это легко проследить, если сделать выборку трех элементов из множества, состоящего всего из 4 объектов (от 1-го до 4-х).

Сочетаний здесь будет всего 4 (это легко проверить и по приведенной выше формуле):

Размещений же окажется гораздо больше:

123, 132, 321, 312, 231, 213, 234, 243, 324, 342 и т.д.

Существует формула, позволяющая подсчитать возможное количество размещений в представленном множестве:

Для нашего примера посчитаем количество потенциальных размещений:

Получается, что для состоящего из 4-х элементов множества существует 4 сочетания и целых 24 размещения.

Для тех, кто увлекается спортивными ставками, эти знания могут пригодится для того, чтобы рассчитать шансы на выигрыш.

Например, в турнире участвует 6 команд. Необходимо определить количество возможных комбинаций троек призеров кубка.

Обозначим названия команд буквами: А, Б, В, Г, Д, Е.

Сначала определим команду, которая станет золотым призером чемпионата. Таких вариантов, очевидно, 6: А, Б, В, Г, Д, Е.

Затем выбираем один из вариантов (пусть это будет комбинация, в которой золото принадлежит команде А), и определяем для него потенциального серебряного призера. Таких комбинаций уже окажется всего 5, так как одна команда уже записана на 1-м месте: АБ, АВ, АГ, АД, АЕ.

Такую пятерку вариаций можно сформировать для каждой из команд. То есть всего претендентов на серебро оказывается 30 (5*6).

Для каждой двойки первых призеров (чемпион-серебряный призер) можно составить только 4 комбинации с бронзовым призером. Первые два места уже распределены, так что остается 4 команды (6-2). Подберем комбинации для варианта АБ: АБВ, АБГ, АБД, АБЕ.

Мы уже подсчитали выше количество возможных комбинаций для первых двух мест – их оказалось 30. Теперь это число умножаем на 4 – получаем 120.

Выходит, что если в турнире участвует 6 команд, вариантов их размещения по первым трем местам может быть целых 120. Угадать призеров не так просто.

Сочетания и размещения: в чем же разница?

И сочетания, и размещения являются выборкой из определённого множества. Принципиальная разница между понятиями заключается лишь в том, что в случае сочетаний порядок расположения элементов не имеет значения, а в случае размещений он важен. Именно поэтому в пределах одного и того же множества количество сочетаний всегда оказывается меньше числа размещений.

Источник

Разница между сочетанием и размещением

Б. Паскаль и Ферма, изучая теорию азартных игр, были основателями нового раздела математики, называемого комбинаторикой. В ней изучается, какое количество комбинаций заданного типа можно составить из предложенных элементов.

Определение

Сочетания — соединения, каждое из которых составлено из k1 элементов, выбранных из n1 различных элементов, состав которых отличается хотя бы на один элемент.

Размещения — cоединения, каждое из которых составлено из k1 элементов, взятых из n1 различных элементов, у которых состав элементов или их порядок отличают их друг от друга.

Сравнение

Сочетания — соединения, содержащие k1 элементов, выбранных из n1 различных элементов. Сочетания отличаются друг от друга хотя бы на один элемент. Порядок следования элементов не важен. Число сочетаний равно n1 элементов.

Наборы, которых отличает только порядок следования элементов, но не состав, считаются одинаковыми. Отличие сочетаний друг от друга составом, но не порядком следования элементов.

Пример. Сочетание — нужно выбрать 3 предмета из 6. Есть предметы с номерами от 1 до 6. Выбираем из этого набора предметы в любом порядке с номерами 1, 4 и 6. Это и есть сочетание.

Размещениями называют соединения, каждое из которых содержит k1 элементов, взятых из n1 различных элементов, которых отличает друг от друга порядок или состав элементов. В размещениях не должно быть дубликатов.

Источник

Чем отличаются сочетания и размещения элементов

Таким образом, полученные комбинации удовлетворяют различным условиям.

В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.

Предварительно познакомимся с понятием факториала.

Произведение всех натуральных чисел от 1 до n включительно называют

Комбинация из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками.

Число перестановок можно вычислить по формуле

Запишем эту формулу в факториальной форме:

Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:

Источник

Комбинаторика: размещения и сочетания

При решении задач по комбинаторике используют следующие важные понятия

Факториалы

Перестановки

Размещения

Сочетания

Размещения

Рассмотрим следующую задачу.

На первое место можно положить одну из 9 карточек. Для этого есть 9 способов. В каждом из этих 9 способов на второе место можно положить одну из оставшихся 8 карточек. Таким образом, существует

способа, чтобы положить карточки на первое и второе места. В каждом из этих 72 способов на третье место можно положить одну из оставшихся 7 карточек. Следовательно, существует

способа, чтобы положить карточки на первое, второе и третье места. В каждом из этих 504 способов на четвертое место можно положить одну из оставшихся 6 карточек. Отсюда вытекает, что существует

различных способа, чтобы выложить в ряд 4 карточки из набора, состоящего из 9 пронумерованных карточек. Таким образом, при выкладывании карточек можно получить 3024 различных четырехзначных числа.

При решении задачи мы провели подсчет числа способов раскладывания карточек, который является частным случаем общего метода подсчета числа размещений и заключается в следующем.

В соответствии с определением факториала, формулу (1) можно также записать в виде:

В задаче множеством из n элементов является исходный набор из 9 пронумерованных карточек, а упорядоченным подмножеством из k элементов – 4 карточки, выложенные в ряд.

Таким образом, при решении задачи мы на частном примере подсчитали, чему равно число размещений из 9 элементов по 4 элемента, т.е. число

В соответствии с формулой (1),

что и было получено в задаче.

смысл которой заключается в следующем.

Сочетания

Число сочетаний из n элементов по k элементов обозначается символом

Таким образом, справедлива формула:

откуда вытекает формула

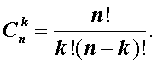(2)

Теперь рассмотрим несколько примеров подсчета числа сочетаний, которые непосредственно вытекают из формулы (2):

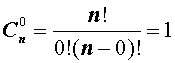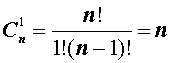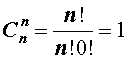В заключение приведем часто используемое равенство, также непосредственно вытекающее из формулы (2):

С понятиями факториала числа n и перестановок из n элементов можно познакомиться в разделе «Комбинаторика: факториалы и перестановки» нашего справочника.

Источник

Сочетания. Размещения. Перестановки

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

Где ( ).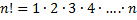

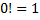
Рассмотрим пример: сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая цифра входит в изображение числа только один раз?

.

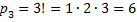
Или такой пример. Порядок выступления семи участников на студенческой конференции определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?

Решение: каждый вариант жеребьевки отличается только порядком участников, то есть является перестановкой из 7 элементов. Их число находится

.

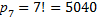
Пример. К кассе за получением денег подошли одновременно 4 человека. Сколькими способами они могут выстроиться в очередь?

Решение: очередь состоит из 4 различных лиц, поэтому в каждом способе составления очереди учитывается порядок их расположения. Таким образом, имеют место перестановки из четырех человек, их число равно

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо их порядком, либо составом элементов.

Число всех возможных размещений рассчитывается

Пример: сколько можно составить сигналов из 6 флажков различного цвета, взятых по два?

Пример: расписание одного дня состоит из пяти уроков. Определить число вариантов расписания при выборе из 11 дисциплин.

Решение: каждый вариант расписания представляет набор 5 дисциплин из 11, отличающийся от других вариантов, как составом дисциплин, так и порядком их следования, то есть является размещением из 11 элементов по 5. Число вариантов расписания находят по формуле

Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний

Пример: сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?

Пример: в шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?

Решение: каждая партия играется двумя участниками из 16 и отличается только составом пар участников, то есть представляет собой сочетание из 16 элементов по два

Пример: имеется 6 штаммов бактерий. Для определения скорости их роста необходимо выбрать три штамма. Сколькими способами можно это сделать?

Решение: способы отбора считаются различными, если каждый отобранный штамм различается хотя бы одним элементом. Это число

То есть имеется 20 способов.

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством

При решении задач комбинаторики используют следующие правила.

Правило суммы: если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно 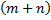способами.

Правило произведения: если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А,В) в указанном порядке может быть выбрана 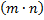способами.

Пример: в студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?

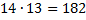
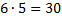
Решение: по правилу умножения двух девушек можно выбрать способами, а двух юношей способами. Следует выбрать двух студентов одного пола: двух девушек или двух юношей. Согласно правилу сложения таких способов выбора будет 182 + 30 = 212.

Контрольные вопросы

1. Что называют графом?

2. Какие вершины графа можно назвать смежными?

3. Возможно ли начертить граф с нечетным числом нечетных вершин?

4. Чем определяется полный граф?

5. Что называют перестановками, размещениями, сочетаниями?

6. Сформулировать правила суммы и произведения.

Источник