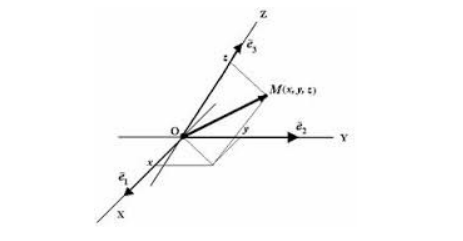
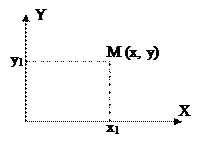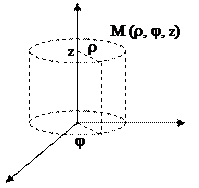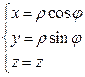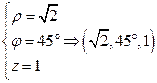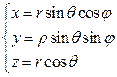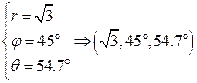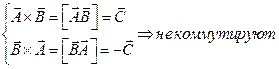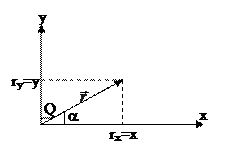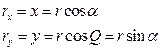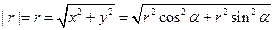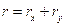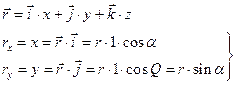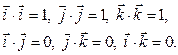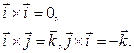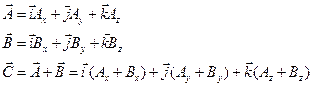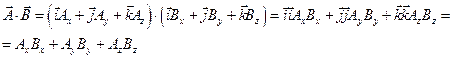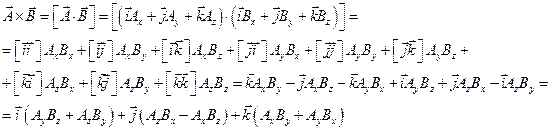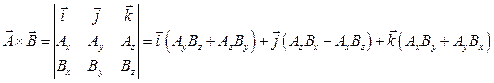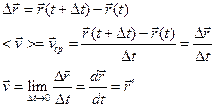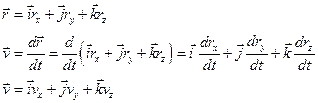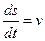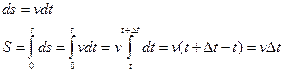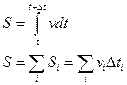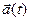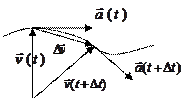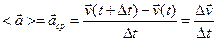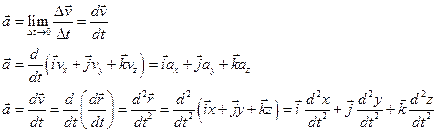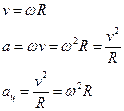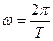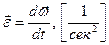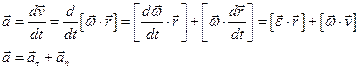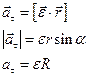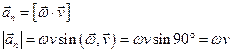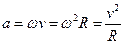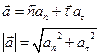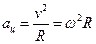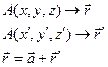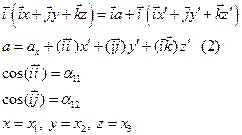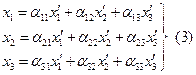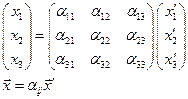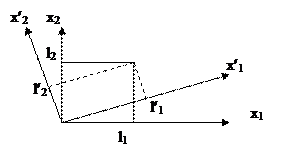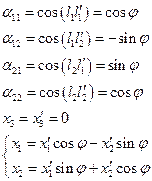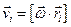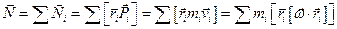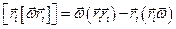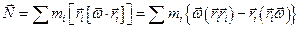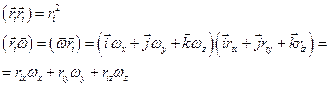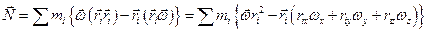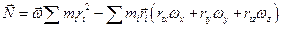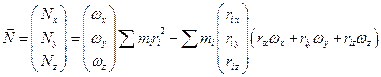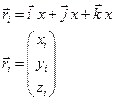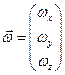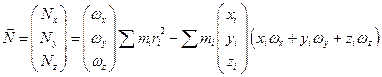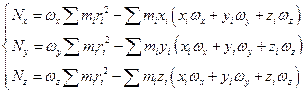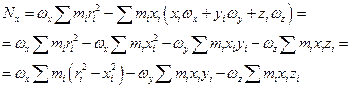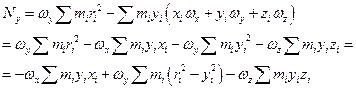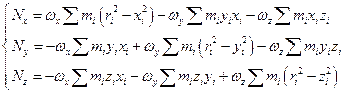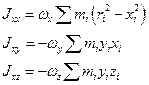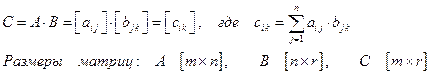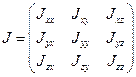Чем отличаются понятия система отсчета и система координат
Механическое движение и его характеристики
теория по физике 🧲 кинематика
Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.
Основная задача механики — определение положение тела в пространстве в любой момент времени.
Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение и его виды
По характеру движения точек тела выделяют три вида механического движения:
По типу линии, вдоль которой движется тело, выделяют два вида движения:
По скорости выделяют два вида движения:
По ускорению выделяют три вида движения:
Что нужно для описания механического движения?
Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.
Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.
Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.
Тело отсчета — тело, относительно которого рассматривается движение.
Часы — прибор для отсчета времени. Время измеряется в секундах (с).
При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.
Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.
Виды систем координат
В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:
Способы описания механического движения
Описать механическое движение можно двумя способами:
Координатный способ
Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:
Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.
Векторный способ
Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.
Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:
Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.
Характеристики механического движения
Движение материальной точки характеризуют три физические величины:
Перемещение
Траектория — линия, которую описывает тело во время движения.
Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).
Путь есть функция времени:
Модуль перемещения — длина вектора перемещения. Обозначается как |Δ r |. Единица измерения — метры (м).
Модуль перемещения необязательно должен совпадать с длиной пути.
Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.
Путь равен длине окружности. Поэтому:
Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.
Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?
Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:
Скорость
Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.
Скорость характеризуется не только направлением вектора скорости, но и его модулем.
Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).
Математическое определение модуля скорости:
Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:
Ускорение
Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.
Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с 2 ).
Математическое определение модуля скорости:

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:
Проекция вектора перемещения на ось координат
Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.
Проекция вектора на ось OX:
Проекция вектора на ось OY:
Знаки проекций перемещения
Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.
Модуль перемещения — длина вектора перемещения:
Модуль перемещения измеряется в метрах (м).
Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:
Выразив проекции вектора перемещения через координаты, эта формула примет вид:
Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:
Общий вид уравнений координат:
Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.
Определяем координаты начальной точки вектора:
Определяем координаты конечной точки вектора:
Проекция вектора перемещения на ось OX:
Проекция вектора перемещения на ось OY:
Применяем формулу для вычисления модуля вектора перемещения:
Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.
Извлекаем известные данные:
Для определения координаты точки В понадобятся формулы:
Выразим из них координаты конечного положения точки:
Точка В имеет координаты (5; 10).
Алгоритм решения
Решение
Записываем исходные данные:
Записываем формулу ускорения:
Так как начальная скорость равна 0, эта формула принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Отсюда скорость равна:
Подставляем имеющиеся данные и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Чем отличаются понятия система отсчета и система координат
Система отсчёта — это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел.
Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями
Движущиеся тела изменяют своё положение относительно других тел в пространстве с течением времени. Положение автомобиля, мчащегося по шоссе, изменяется относительно указателей на километровых столбах, положение корабля, плывущего в море недалеко от берега, меняется относительно береговой линии, а о движении самолёта, летящего над землей, можно судить по изменению его положения относительно поверхности Земли. Можно показать, что одно и то же тело при одном и том же движении может одновременно по-разному перемещаться относительно разных тел.
Абсолютная система отсчёта
Часто в физике какую-то СО считают наиболее удобной (привилегированной) в рамках решения данной задачи — это определяется простотой расчётов либо записи уравнений динамики тел и полей в ней. Обычно такая возможность связана с симметрией задачи.
С другой стороны, ранее считалось, что существует некая «фундаментальная» система отсчёта, простота записи в которой законов природы выделяет её из всех остальных систем. Например, физики XIX в. считали что, система, относительно которой покоится эфир электродинамики Максвелла, является привилегированной, и поэтому она была названа Абсолютной Системой Отсчета (АСО). В современных представлениях никакой системы отсчёта, выделенной именно таким способом, не существует, так как законы природы, выраженные в тензорной форме, имеют один и тот же вид во всех системах отсчёта — то есть во всех точках пространства и во все моменты времени. Это условие — локальная пространственно-временная инвариантность — является одним из проверяемых оснований физики.
Иногда абсолютной системой отсчета называют систему, связанную с реликтовым излучением, то есть инерциальную систему отсчета, в которой реликтовое излучение не имеет дипольной анизотропии.
Система отсчета
Система отсчета – это совокупность тела отсчета, со связанной с ним системой координат и прибором для измерения времени.
Что такое система отсчета. Афинная и декартовая системы координат
Если рассматривать все системы отсчета относительно кинематики – они аналогичные. В кинематике не указываются преимущества одной системы отсчета при сравнении с другой. Для удобства решения выбирается наиболее приемлемая система.
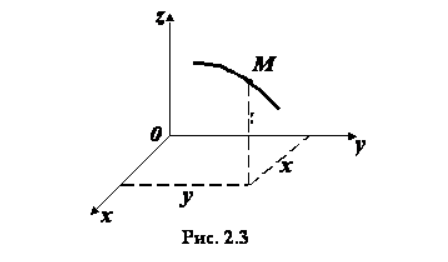
Чтобы описать пространство, в котором происходит движение материальной точки, система отсчета связывается с пространственной системой координат.
Системой пространственных координат называют совокупность определений, которая может реализовать метод координат, то есть определение положения точки или тела с помощью чисел или символов.
Числа, способные указать положение выбранной точки в трехмерном пространстве, называются координатами этой точки.
Аффинная система координат – это три линейно независимых вектора (координатных осей), выходящие из одной точки, то есть из начала отсчета.
Чтобы однозначно определить положение точки М в пространстве, то предполагают наличие зависимости радиус-вектора r → от параметра t (времени) таким образом, что каждому значению параметра t соответствует одно значение функции:
Данное равенство получило название кинематического уравнения движения материальной точки М в векторной форме.
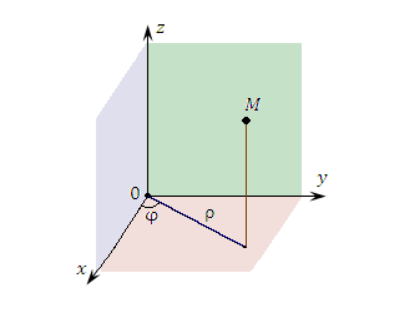
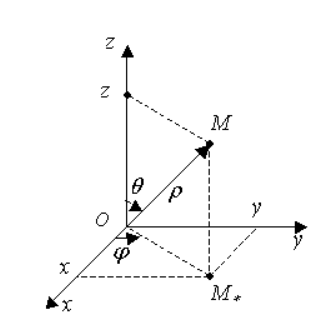
Цилиндрическая и сферическая системы координат
Чтобы описать криволинейное и аффинное движение, применяют криволинейные системы координат, которые упрощают форму записи законов движения тел для облегчения вычисления. Чаще всего используют цилиндрические и сферические системы координат.
Связь между декартовыми и цилиндрическими координатами может быть задана при помощи формул:
Рисунок 4 показывает, что можно вывести формулы, связывающие сферические и декартовые координаты:
Рисунок 4 . Сферические координаты точки М
Имеются другие системы криволинейных координат, с помощью которых возможно нахождение координат заданной точки: параболические, гиперболические, эллиптические и другие.
Система отсчета выбирается индивидуально относительно каждого случая в отдельности, учитывается особенность движения тела, с помощью которой определяется наиболее простой закон движения заданного тела или точки.
Чем различаются понятия система отсчета и система координат?
Чем различаются понятия система отсчета и система координат?
Система отсчета начинается с нуля, а система координат, это все числа на прямой.
Систему отсчета создают тело отсчета, система координат(!
) и способ измерения времени.
То есть система отсчета включает в себя систему координат.
Из чего состоит система отсчета?
Из чего состоит система отсчета?
Примеры системы отсчета?
Примеры системы отсчета.
Примеры неинерциальных системы отсчетов?
Примеры неинерциальных системы отсчетов.
Что такое материальная точка и в каком случае тело можно принять за мат.
Точку, для чего введено это понятие?
Что такое система отсчета?
Для чего она вводится?
Какие системы координат вы знаете?
Что называют траекторией движения?
Что такое путь и перемещение?
В чем отличие пути от перемещения?
Какая система отсчета называется инерциальной?
Какая система отсчета называется инерциальной?
Почему система отсчета, связанная с Землей, строго говоря, не является инерциальной?
Два события в некоторой инерциальной системе отсчета происходят в одной точке одновременно?
Два события в некоторой инерциальной системе отсчета происходят в одной точке одновременно.
Будут ли эти события одновременными в другой инерциальной системе отсчета.
Какие системы отсчета называются инерциальными?
Какие системы отсчета называются инерциальными?
Из чего состоит система отсчета?
Из чего состоит система отсчета?
(возможно несколько правильных ответов) а) движущееся тело б) часы в) тело отсчета г) система координат.
Что такое материальная точка и в каком случае тело можно принять за мат.
Точку, для чего введено это понятие?
Что такое система отсчета?
Для чего она вводится?
Какие системы координат вы знаете?
Что называют траекторией движения?
Что такое путь и перемещение?
В чем отличие пути от перемещения?
Из чего состоит система отсчета?
Из чего состоит система отсчета.
19 метров ну как вроде.
M = 1500 кг Из уравнения a / 2 = 2, а = 4 м / с² F = m * a = 1500 * 4 = 6000 H = = = = = = = = = = = = = = = = = = = = = =.
Подали два числа затем умножи и все.
Из формулы плотности p = m / v. Выражаем массу m = pv, получаем 0, 001м ^ 3 * 7800 = 7, 8кг. Q = cm / \ t Q = 500 * 7, 8 * 50 = 195000ДЖ или 195кДЖ.
Системы координат. Системы отсчета
Все механические процессы происходят в пространстве и времени. Это находит отражение в любом механическом законе.
Положение тела в пространстве может быть определено только по отношению к другим телам. Тело отсчета – тело (система неподвижных тел), которое служит для определения положения интересующего нас тела.
Кроме тела отсчета нужна система, которая обеспечивала бы «адреса» других тел. С этой целью вводится система координат. Система координат позволяет определить положение тела в пространстве. Но нужна еще совокупность тела отсчета, связанных с ним координат и синхронизирующих часов – это система отсчета.
Заметим, что удачный выбор системы координат существенно облегчает решение задачи. Рассмотрим основные типы систем координат:
2. Цилиндрическая система координат:
Задание: Найти координаты точки (1,1,1) в цилиндрической системе координат.
3. Сферическая система координат:
Задание: Найти координаты точки (1,1,1) в сферической системе координат.
Формулы, связывающие координаты точки в одной системе отсчета с координатами в другой системе, называют формулами преобразования координат.
Скалярные, векторные величины. Действия над ними. Вычисление компонент вектора. Орты.
Для удобства координаты точки в любой системе координат будем обозначать одной буквой:
Вектор – направленный отрезок прямой, у которого один конец называется началом, а другой конец – концом. Модуль, направление, точка приложения, нулевой вектор.
Два вектора равны, если они имеют одинаковые модули и направление.
Противоположным вектору 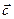
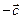
Действия над векторами:
a. Правило треугольника 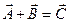
b. Правило прямоугольника;
Если при действии над векторами результат не изменяется при перестановке векторов, то говорят, что вектора обладают свойством коммутативности относительно этого действия.
2. Разность векторов 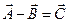
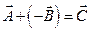
3. Умножение вектора на число 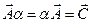
4. Скалярное произведение векторов:
Скалярным произведение векторов называют произведение модулей этих векторов на косинус угла между ними. Т.е. результат скалярного произведения – скаляр.
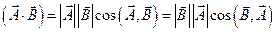
Обладает свойством коммутативности.
Пример: 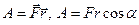
5. Векторное произведение:
В результате векторного произведения получается вектор, модуль которого равен произведению модулей перемножающихся векторов на синус угла между ними. Результирующий вектор направлен перпендикулярно плоскости перемножаемых векторов и направлен в сторону движения правого винта, если вращать его от первого вектора ко второму по кратчайшему пути.
Модуль вектора C равен площади параллелограмма, построенного на A и B.
Компоненты векторных величин.
Скалярное и векторное произведение орт:
Скалярные произведения одноименных орт равны 1, разноименных – 0.
Векторное произведение одноименных орт равно 0. Модуль векторного произведения разноименных орт равен 1.
Действия над векторами в координатной форме.
Компонент суммы двух векторов – сумма компонент слагаемых.
Радиус вектор – вектор, проведенный из начала координат в данную точку.
Перемещение и скорость в векторной и координатной формах.
Траектория – линия, вдоль которой движется тело.
Путь – расстояние вдоль траектории.
Перемещение – кратчайшее расстояние.
Вектором мгновенной скорости называют вектор, равный производной радиус-вектора по времени (направлен по касательной).
При прямолинейном движении 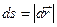
Абсолютное значение скорости (модуль):

Если 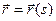
Ускорение в векторной и координатной формах.
вектор среднего ускорения (скорость изменения скорости)
Изменение линейной скорости по направлению (меняется только направление).
Вектор ускорения – вторая производная вектора перемещения по времени.
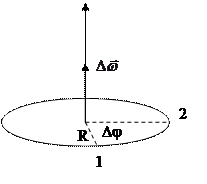
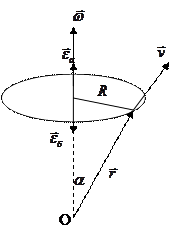
Кинематика вращательной точки. Угловая скорость.
Т – период (время одного оборота).
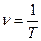
Модуль 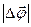
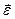
a) При равноускоренном движении вектор 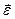
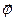
b) При равнозамедленном – в обратную.
Вектора r, v и a называют естественными или полярными векторами.
Вектора 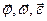
Аксиальные вектора введены для объяснения физических процессов при вращательном движении. Они, так же как и полярные вектора подчиняются правилу сложения векторов.
Связь между линейными и угловыми величинами.
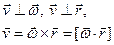
По определению векторного произведения 
an=aц – изменение скорости по направлению за единицу времени.
at – изменение скорости по модулю за единицу времени. При равномерном движении at=0.
Преобразование координат и компонент векторов.
Формулы, связывающие координаты точки в одной системе координат с координатами в другой называются преобразование координат.
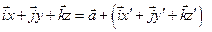 | (1) |
Для определения компоненты x умножим скалярно (1) на i:
Тогда (2) запишем для случая ax=0 (поворот):
Пример: Преобразование координат для двухмерного случая.
Значение скалярной величины определяется одним числом.
Значение вектора определяется тремя числами, которые называют компоненты вектора.
Более общее определение вектора:
Вектор – это упорядоченная совокупность трех чисел, зависящих от системы координат и преобразующихся при повороте системы отсчета так же, как преобразуются компоненты вектора.
При параллельном переносе компоненты вектора не изменяются:
Вектор тот же, но системы разные.
Величины, значения которых не изменяются при преобразованиях, называются инвариантами.
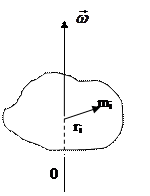
Вращение вокруг неподвижной оси.
Для точки mi имеем:
Рассмотрим момент импульса относительно оси 0. Общий момент импульса равен:

Аналогично преобразуем Nz .
Введем инерциальные коэффициенты или моменты инерции:
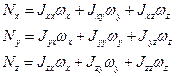
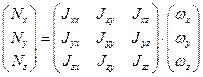
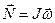
Здесь обозначения аналогичные.
Совокупность величин 
Тензор симметричный, т.е. 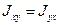
Главные оси тензора инерции.
Симметричный тензор можно представить наглядно в виде эллипсоида, в данном случае эллипсоида инерции.
Тензор (второго ранга) – упорядоченная система 9 чисел, которые связывают два вектора.
Вектор (тензор первого ранга)– упорядоченная система трех чисел, которые преобразуются при изменении системы координат.
Скаляр (тензор нулевого ранга)– число, не изменяющееся при изменении системы координат.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет