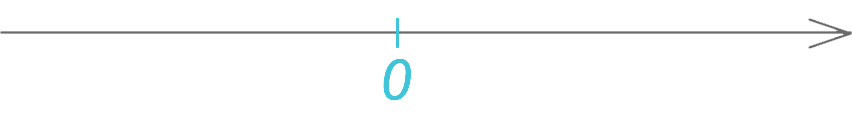Чем отличаются положительные и отрицательные числа
Какие числа называются целыми
Определение целых чисел
Что важно знать о целых числах:
Целые числа на числовой оси выглядят так:
На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.
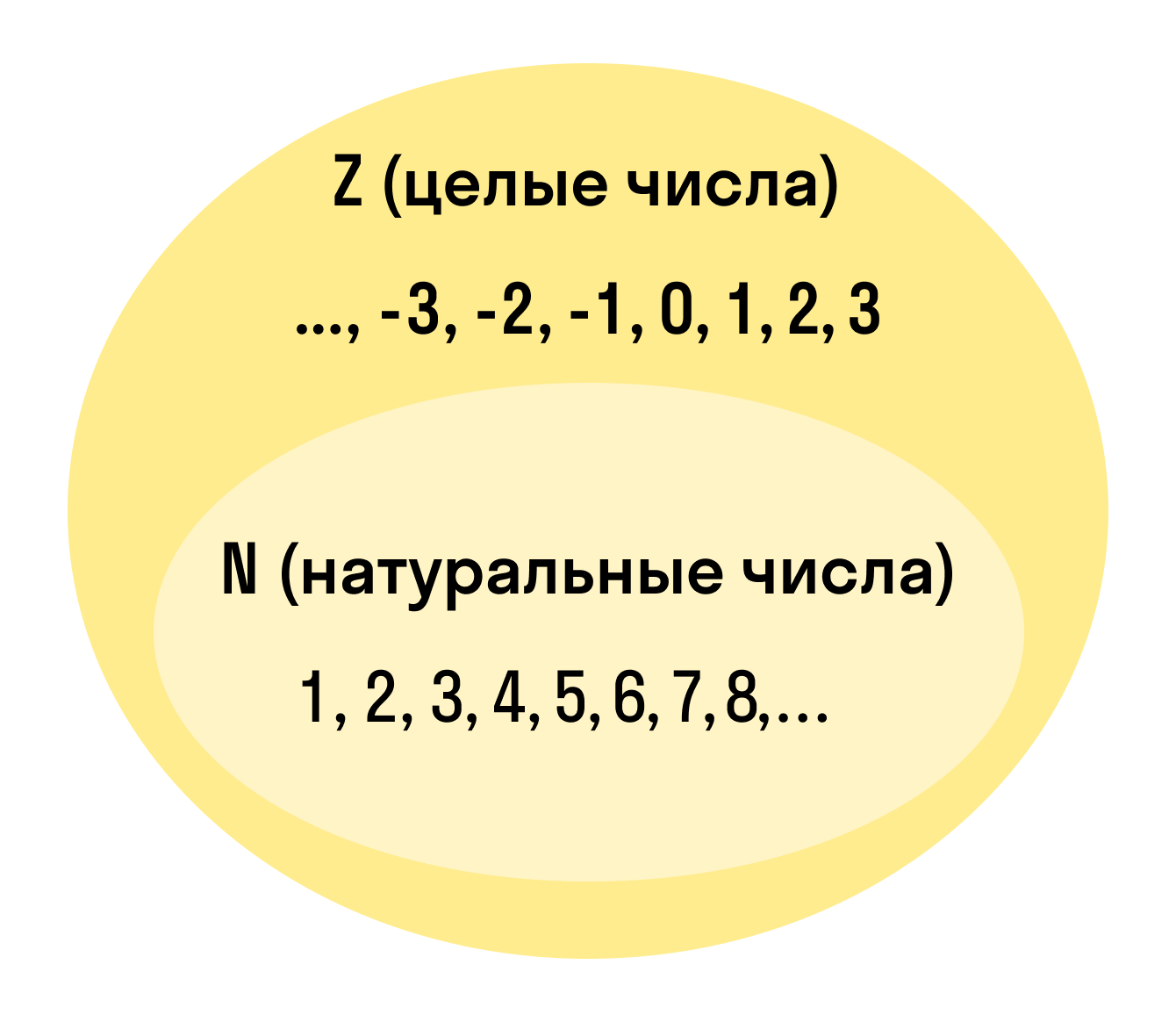
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и противоположные натуральным отрицательные числа. Множество целых чисел обозначают Z.
Выглядит эти ребята вот так:
Последовательность целых чисел можно записать так:
Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:
Положительные и отрицательные числа, определение, примеры.
Сейчас мы разберем положительные и отрицательные числа. Сначала дадим определения, введем обозначения, после чего приведем примеры положительных и отрицательных чисел. Также остановимся на смысловой нагрузке, которую несут в себе положительные и отрицательные числа.
Навигация по странице.
Положительные и отрицательные числа – определения и примеры
Дать определение положительных и отрицательных чисел нам поможет координатная прямая. Для удобства будем считать, что она расположена горизонтально и направлена слева направо.
Числа, которые соответствуют точкам координатной прямой, лежащим правее начала отсчета, называют положительными.
Числа, которые соответствуют точкам координатной прямой, лежащим левее начала отсчета называю отрицательными.
Число нуль, соответствующее началу отсчета, не является ни положительным, ни отрицательным числом.
Из определения отрицательных и положительных чисел следует, что множество всех отрицательных чисел представляет собой множество чисел, противоположных всем положительным числам (при необходимости смотрите статью противоположные числа). Следовательно, отрицательные числа всегда записываются со знаком минус.
Числа со знаком плюс называют положительными, а со знаком минус – отрицательными.
Существует еще одно определение положительных и отрицательных чисел, основанное на сравнении чисел. Чтобы дать это определение, достаточно лишь вспомнить, что точка на координатной прямой, соответствующая большему числу, лежит правее точки, соответствующей меньшему числу.
Положительные числа – это числа, которые больше нуля, а отрицательные числа – это числа, меньшие нуля.
Таким образом, нуль как бы отделяет положительные числа от отрицательных.
Конечно же, следует еще остановиться на правилах чтения положительных и отрицательных чисел. Если число записано со знаком + или −, то произносят название знака, после чего произносят число. Например, +8 читается как плюс восемь, а 
Интерпретация положительных и отрицательных чисел
Мы уже достаточно долго описываем положительные и отрицательные числа. Однако неплохо было бы знать, какой смысл они несут в себе? Давайте разберемся с этим вопросом.
Положительные числа можно интерпретировать как приход, как прибавку, как увеличение какой-либо величины и тому подобное. Отрицательные числа, в свою очередь, означают строго противоположное – расход, недостаток, долг, уменьшение какой-либо величины и т.п. Разберемся с этим на примерах.
Положительные и отрицательные числа
Чтобы понять, что из себя представляют положительные и отрицательные числа, давайте для начала начертим координатную прямую и отметим на ней точку 0 (ноль), которая считается началом отсчета.
Расположим ось в более привычном горизонтальном виде. Стрелка показывает положительное направление прямой (слева направо).
Сразу обратим внимание, что число “ноль” не относится ни к положительным, ни к отрицательным числам.
Положительные числа
Если мы начнем отмерять отрезки справа от нуля, то полученные отметки будут соответствовать положительным числам, равным расстояния от 0 до этих отметок. Таким образом мы получили числовую ось.
Полная запись положительных чисел включает знак “+” спереди, то есть +3, +7, +12, +21 и т.д. Но “плюс” обычно опускается и просто подразумевается:
Примечание: любое положительное число больше нуля.
Отрицательные числа
Если мы начнем отмерять отрезки слева от нуля, то вместо положительных получатся отрицательные числа, т.к. мы будем двигаться в противоположную от направления прямой сторону.
Примечание: любое отрицательное число меньше нуля.
Отрицательные числа как и положительные нужны для выражения различных математических, физических, экономических и прочих величин. Например:
Положительные и отрицательные числа: определение, примеры
В этом материале мы объясним, что такое положительные и отрицательные числа. После того, как будут сформулированы определения, мы покажем на примерах, что это такое, и раскроем основной смысл этих понятий.
Что такое положительные и отрицательные числа
Для того чтобы объяснить основные определения, нам понадобится координатная прямая. Она будет расположена горизонтально и направлено слева направо: так будет удобнее для понимания.
Положительные числа – это те числа, которые соответствуют точкам в той части координатной прямой, которая расположена справа от начала отсчета.
Отрицательные числа – это те числа, которые соотносятся с точками в части координатной прямой, расположенной с левой стороны от начала отсчета (нуля).
Нуль, от которого выбираем направления, сам по себе не относится ни к отрицательным, ни к положительным числам.
Из данных выше определений следует, что положительные и отрицательные числа образуют некие множества, противоположные друг другу (положительные противопоставляются отрицательным, и наоборот). Ранее мы об этом уже упоминали в рамках статьи о противоположных числах.
Мы всегда записываем отрицательные числа с минусом.
В литературе также можно встретить определения положительных и отрицательных чисел, данные на основе наличия у них того или иного знака.
Положительное число – это число, имеющее знак плюс, а отрицательное – имеющее знак минус.
Положительные числа – это все числа, значение которых больше нуля. Отрицательные числа – это все числа, меньшие нуля.
Выходит, что нуль является своеобразным разделителем: он отделяет отрицательные числа от положительных.
Основной смысл положительных и отрицательных чисел
Мы уже дали основные определения, но для того, чтобы делать верные подсчеты, необходимо понять сам смысл положительности или отрицательности числа. Попробуем помочь вам это сделать.
Алгебра
Отрицательные числа. Целые отрицательные числа.
Дробные отрицательные числа. Положительные числа.
Отрицательные числа появляются, когда из меньшего числа вычитают большее, например:
Знак «минус» перед 5 показывает, что это число отрицательное.
Было 10 рублей. Купили некую вещь за 15, одолжив 5 руб. Теперь имеем минус 5 руб., которые позже потребуется вернуть. А можно представить графически, на линейке:
Ряд целых отрицательных чисел бесконечен:
Целые числа — это натуральные числа, целые отрицательные числа и ноль:
Дробные отрицательные числа появляются, например, когда из меньшего дробного числа вычитают большее:
Можно также сказать, что дробные отрицательные числа появляются в результате деления целого отрицательного числа на натуральное:
Положительные числа ( целые и дробные ) в противоположность отрицательным числам ( целым и дробным )рассматриваются в арифметике.
Рациональные числа – это положительные и отрицательные числа (целые и дробные) и ноль. Более точное определение рациональных чисел, принятое в математике, следующее:
Действия с отрицательными и положительными числами
Абсолютная величина (модуль). Сложение.
Вычитание. Умножение. Деление.
Абсолютная величина ( модуль ). Для отрицательного числа – это положительное число, получаемое от перемены его знака с « – » на « + »; для положительного числа и нуля – само это число.
Для обозначения абсолютной величины (модуля) числа используются две прямые черты, внутри которых записывается это число.
П р и м е р ы : | – 5 | = 5, | 7 | = 7, | 0 | = 0.
Сложение:
1) при сложении двух чисел с одинаковыми знаками складываются
их абсолютные величины и перед суммой ставится общий знак.
( – 6 ) + ( – 5 ) = – 11 .
2) при сложении двух чисел с разными знаками их абсолютные
величины вычитаются ( из большей меньшая ) и ставится знак
числа с большей абсолютной величиной.
( – 6 ) + ( + 3 ) = – 3 .
Вычитание. Можно заменить вычитание двух чисел сложением, при этом уменьшаемое сохраняет свой знак, а вычитаемое берётся с обратным знаком.
( + 8 ) – ( + 5 ) = ( + 8 ) + ( – 5 ) = 3;
( + 8 ) – ( – 5 ) = ( + 8 ) + ( + 5 ) = 13;
( – 8 ) – ( – 5 ) = ( – 8 ) + ( + 5 ) = – 3;
( – 8 ) – ( + 5 ) = ( – 8 ) + ( – 5 ) = – 13;
Полезна следующая схема (правила знаков при умножении):
Надо просто посчитать количество сомножителей с минусом. Если их количество кратно двум, результат умножения будет положительным. Каждый добавленный отрицательный сомножитель меняет знак результата:
Здесь действуют те же правила знаков, что и при умножении:
Понятно почему: деление можно заменить умножением на обратное число.
П р и м е р : ( – 12 ) : ( + 4 ) = – 3
Принципиальной разницы между делением и умножением нет. Отсюда понятно, что знак результата умножения и деления нескольких чисел также будет зависеть от того четно или нечетно количество отрицательных сомножителей и делителей (делимых).
Одночлен. Коэффициент. Числовой множитель. Подобные одночлены.
Степень одночлена. Сложение одночленов. Приведение подобных членов.
Вынесение за скобки. Умножение одночленов. Деление одночленов.
Многочлен. Степень многочлена. Умножение сумм и многочленов.
Одночлен – это произведение двух или нескольких сомножителей, каждый из которых либо число, либо буква, либо степень буквы. Например,
Единственное число или единственная буква также могут считаться одночленом. Любой множитель в одночлене называется коэффициентом. Часто коэффициентом называют лишь числовой множитель.
Одночлены называются подобными, если они одинаковы или отличаются лишь коэффициентами.
8 a 2 и 3 a 2
Поэтому, если два или несколько одночленов имеют одинаковые буквы или их степени, они также подобны.
Степень одночлена – это сумма показателей степеней всех его букв.
Сложение одночленов. Если среди суммы одночленов есть подобные, то сумма может быть приведена к более простому виду:
Эта операция называется приведением подобных членов. Выполненное здесь действие называется также вынесением за скобки.
Можно рассуждать так: произведение x 3 y 2 равно какому-то числу, допустим, z. Заменим в вышеприведенном уравнении x 3 y 2 на z:
a x 3 y 2 – 5 b 3 x 3 y 2 + c 5 x 3 y 2 = a z – 5 b 3 z + c 5 z.
Теперь этот z, пользуясь распределительным законом, можно вынести за скобки:
( a – 5 b 3 + c 5 ) z.
Теперь, заменив z обратно на x 3 y 2 :
( a – 5 b 3 + c 5 ) x 3 y 2
То есть, выражением x 3 y 2 мы оперируем как единым (одним) числом.
Умножение одночленов. Произведение нескольких одночленов можно упростить, если только оно содержит степени одних и тех же букв или числовые коэффициенты. В этом случае показатели степеней складываются, а числовые коэффициенты перемножаются.
Здесь тоже никакой засады: независимо от скобок мы перемножаем одинаковые буквы:
Деление одночленов. Частное двух одночленов можно упростить, если делимое и делитель имеют некоторые степени одних и тех же букв или числовые коэффициенты. В этом случае показатель степени делителя вычитается из показателя степени делимого, а числовой коэффициент делимого делится на числовой коэффициент делителя.
Умножение сумм и многочленов. Произведение суммы двух или нескольких выражений на любое выражение равно сумме произведений каждого из слагаемых на это выражение:
Вместо букв p, q, r, a может быть взято любое выражение.
( x+ y+ z )( a+ b ) = x( a+ b ) + y( a+ b ) + z( a+ b ) =
Произведение сумм равно сумме всех возможных произведений каждого слагаемого одной суммы на каждое слагаемое другой суммы.
Докажем:
площадь прямоугольника равна произведению сумм отрезков x + y + z и
Из правил умножения сумм и многочленов легко получить следующие семь формул сокращённого умножения.
Их следует знать наизусть, так как они применяются практически во всех задачах по математике.
Тут соображения те же, что и в предыдущем примере со сложением площадей внутренних прямоугольников. Разница лишь в том, что два внутренних прямоугольника одинаковы. Их суммарная площадь и записывается как 2ab.
Здесь получается так:
Преобразованная же формула a² – 2ab + b² , показывает процесс нахождения этой площади, без нахождения длины c.
[3] ( a + b ) ( a – b ) = a² – b²,
Р е ш е н и е : 99³ = (100 – 1)³ = 1000000 – 3 · 10000 · 1 + 3 · 100 · 1 – 1 = 970299.
1) имеет место равенство: MQ + N = P ;
2) степень многочлена N меньше степени многочлена Q.
Деление многочленов может быть выполнено по следующей схеме: