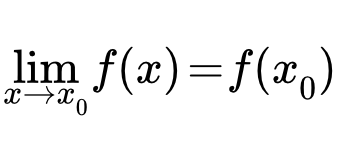Чем отличаются определения непрерывности и предела функции в точке

Чем отличаются определения непрерывности и предела функции в точке

Одним из центральных понятий математического анализа является понятие предела функции в точке. Дадим определение понятия предела функции по Коши или на «языке ε –δ».

Данное определение может быть записано на формализованном языке:

В отдельных случаях способ приближения аргумента x к x ₀ существенно влияет на значение предела функции. Поэтому целесообразно ввести понятия односторонних пределов.

На рисунке 3.1 изображены два важных положения.

2) У данной функции y = f ( x ) в точке x ₀ односторонние пределы совпадают и равны значению функции в этой точке, то есть A – = A + = f ( x ).

С помощью определения предела введём важнейшие понятия математического анализа – бесконечно малой и бесконечно большой величины.

Бесконечно малые и бесконечно большие величины взаимно обратны, то есть если функция α( x ) – бесконечно малая, отличная от нуля, то функция есть бесконечно большая функция и наоборот: если функция f ( x ) – бесконечно большая, то – бесконечно малая.

Рассмотрим определение непрерывности функции в точке.

Если функция y = f ( x ) определена в точке x ₀ и ее окрестности, и при этом выполняется равенство

то функция называется непрерывной в точке x 0 .

Если функция y = f ( x ) непрерывна в каждой точке интервала ( a ; b ), то она называется непрерывной на этом интервале. Если интервал ( a ; b ) совпадает со всей числовой прямой, то функция называется непрерывной на множестве действительных чисел. Если интервал ( a ; b ) совпадает с областью определения функции, то говорят, что функция непрерывна на всей своей области определения. Функция y = f ( x ) называется непрерывной на отрезке [ a ; b ], если она непрерывна на интервале ( a ; b ) и в точке x = a непрерывна справа (то есть ), и в точке x = b непрерывна слева (то есть ).

Важные свойства непрерывных функций можно сформулировать в виде следующих теорем.

Теорема 3.7 (теорема Вейерштрасса). Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений

Следствие. Если функция непрерывна на отрезке, то она на этом отрезке ограничена

Рассмотрим функцию y = f ( x ), которая в точке x ₀ не является непрерывной, то есть имеет в этой точке разрыв. При A – ≠ A + обозначим

1. ω – конечное число точка x ₀ называется точкой неустранимого разрыва 1–го рода функции y = f ( x ), ω – скачком функции (рис. 3.2).

2. (хотя бы один из пределов A + или A – не существует или бесконечен) точка x 0 называется точкой неустранимого разрыва 2–го рода функции – вертикальная асимптота графика функции (рис. 3.3).

При точка x ₀ называется точкой устранимого разрыва 1– го рода. В этом случае функцию в точке x ₀ доопределяют.

Особое значение для исследования поведения графика функции имеют ее пределы на бесконечности.

1. – конечное число y = b – одна горизонтальная асимптота графика функции при и (рис. 3.4).

2. и A * ; B * – конечные числа у графика функции две горизонтальные асимптоты

Источник

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №9. Предел функции в точке. Непрерывность функции.

Перечень вопросов, рассматриваемых в теме

Функциюy = f (x) называют непрерывной в точке х = а, если предел функции y = f (x) при стремлении х к а равен значению функции в точке х = а.

Функция y = f (x) называется непрерывной на промежутке Х, если она непрерывна в каждой точке промежутка.

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

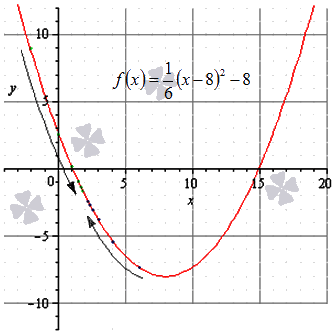
Рассмотрим функции, графики которых изображены на рисунках 1-3.

Воспользуемся построенными графиками функций. Во всех трех случаях изображена одна и та же кривая, тем не менее, это три разные функции.

Ответим на несколько вопросов, касаемых данных функций.

Чем они отличаются друг от друга?

Они отличаются друг от друга своим поведением в точке х = а.

Как ведет себя функция в точке х = а на первом графике?

Для функции у=f(х) при х = а значение функции не существует, функция в указанной точке не определена.

Как ведет себя функция в точке х = а на втором графике?

Для функции у=f(х) при х = а значение функции существует, но оно отличается от естественного значения функции в указанной точке.

Как ведет себя функция в точке х = а на третьем графике?

Для функции у=f(х) при х = а значение функции существует, и оно равно естественному значению функции в указанной точке, то есть b.

Если мы исключим точку х = а из рассмотрения, то все три функции будут тождественными.

В общем случае эта запись выглядит следующим образом:.

Эту запись читаем так: «предел функции y=f(x) при стремлении х к а равен b».

А теперь ответим на такой вопрос: какую из трех рассмотренных функций естественно считать непрерывной в точке х = а?

Непрерывной будет третья функция.

Так как эта функция непрерывна, то она удовлетворяет условию И функцию f (x) называют непрерывной в точке х = а.

Иными словами, функцию y = f (x) называют непрерывной в точке х = а, если предел функции y = f (x) при стремлении х к а равен значению функции в точке х = а.

Функция y = f (x) называется непрерывной на промежутке Х, если она непрерывна в каждой точке промежутка.

При изучении различных функций (линейной, квадратичной, степенной, иррациональной, тригонометрических) мы отмечали, что они являются непрерывными либо на всей числовой прямой, либо на промежутке. Исходя из этого, можно сформулировать следующее утверждение: если выражение f (x) составлено из рациональных, иррациональных, тригонометрических выражений, то функция y = f (x) непрерывна в любой точке, в которой определено выражение f (x).

Для вычисления предела функции в точке, как и для предела на бесконечности, используют правила «предел суммы», «предел произведения», «предел частного».

Правило 1. Предел суммы равен сумме пределов:

Правило 2. Предел произведения равен произведению пределов:

Правило 3. Предел частного равен частному пределов:

Перейдем к практической части.

Примеры и разбор решения заданий тренировочного модуля

Пример 1. Вычислить:

выражение х 3 – 2х 2 + 5х +3 определено в любой точке х, в частности, в точке х = 1. Следовательно, функция у = х 3 – 2х 2 + 5х + 3 непрерывна в точке х = 1, а потому предел функции при стремлении х к 1 равен значению функции в точке х = 1.

.

Пример 2. Используя правила, вычислим .

Решение: функция определена в любой точке , в частности, в точке х = 2. Следовательно, функция у = f (x) непрерывна в точке х = 2, а потому предел функции при стремлении х к 2 равен значению функции в точке х=2. Имеем:

Пример 3. Вычислить.

.

Источник

Непрерывность функций – теоремы и свойства

Определение непрерывности функции

Определение непрерывности справа (слева)
Функция f ( x ) называется непрерывной справа (слева) в точке x ₀ , если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x ₀ равен значению функции в x ₀ :
.

Свойства непрерывных в точке функций

Свойство непрерывности слева и справа
Функция непрерывна в точке тогда и только тогда, когда она непрерывна в справа и слева.

Доказательства свойств приводятся на странице «Свойства непрерывных в точке функций».

Непрерывность сложной функции

Предел сложной функции

Точки разрыва

Определение точки разрыва 1-го рода
Точка называется точкой разрыва первого рода, если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.

Определение скачка функции
Скачком Δ функции в точке называется разность пределов справа и слева
.

Таким образом, точка устранимого разрыва – это точка разрыва 1-го рода, в которой скачек функции равен нулю.

Определение точки разрыва 2-го рода
Точка называется точкой разрыва второго рода, если она не является точкой разрыва 1-го рода. То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.

Свойства функций, непрерывных на отрезке

Вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции
Непрерывная на отрезке функция достигает на нем своих верхней и нижней граней или, что тоже самое, достигает на отрезке своего максимума и минимума.

Обратные функции

Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.

Свойства и непрерывность элементарных функций

Элементарные функции и обратные к ним непрерывны на своей области определения. Далее мы приводим формулировки соответствующих теорем и даем ссылки на их доказательства.

Показательная функция

Логарифм

Экспонента и натуральный логарифм

Степенная функция

Тригонометрические функции

Теорема о непрерывности тригонометрических функций
Тригонометрические функции: синус ( sin x ), косинус ( cos x ), тангенс ( tg x ) и котангенс ( ctg x ), непрерывны на своих областях определения.

Теорема о непрерывности обратных тригонометрических функций
Обратные тригонометрические функции: арксинус ( arcsin x ), арккосинус ( arccos x ), арктангенс ( arctg x ) и арккотангенс ( arcctg x ), непрерывны на своих областях определения.

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Непрерывность функции в точке, разрывы первого и второго рода

Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.

Непрерывность функции в точке

Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.

Решение

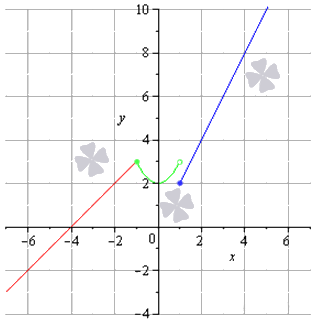
Соответствующая последовательность значений функций выглядит так:

на чертеже они обозначены зеленым цветом.

Соответствующая последовательность функций:

на рисунке обозначена синим цветом.

После вычисления значения функции в заданной точке очевидно выполнение равенства:

Устранимый разрыв первого рода

Решение

Ответ: пределы справа и слева являются равными, а заданная функция в точке х 0 = 5 не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.

Неустранимый разрыв первого рода

Неустранимый разрыв первого рода также определяется точкой скачка функции.

Решение

Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:

Ответ: в конечном счете мы получили:

Нам остается только подготовить чертеж данного задания.

Разрыв второго рода (бесконечный разрыв)

Решение

Зададим произвольную последовательность значений аргумента, сходящуюся к х 0 слева. К примеру:

Ей соответствует последовательность значений функции:

Источник

Пределы и непрерывность функций

Предел функции.

Хорошо, мы определились с поняти функции и теперь можно поговорить про предел функции. Интересно подметить, что наблюдается некая аналогия с пределами последовательностей, а именно согласно определению последовательности, как множества, где каждому элементу поставленно в соответствие действительное число (причем единственное), его можно переписать в терминах функции. И поэтому сразу поставим вопрос, а существуют эквивалентное определение предела функции? И да, существуют, причем два знаменитых определения по Коши и по Гейне. Рассмотрим сначала определение предела функции по Коши:

\[\forall \varepsilon >0\ \exists \delta=\delta(\varepsilon) \in (0, \delta_0) \ \forall x \in \stackrel<0>>(x_0) \to f(x) \in U_<\varepsilon>(A).\]

\[\forall \varepsilon\ \exists \delta=\varepsilon\ \forall x \in (0 1/\varepsilon.\]

Но это не единственное определение предела функции. Рассмотрим определение предела функции по Гейне:

\[\ \in X \\ \lim_ x_n = x_0 \\ \forall n \to x_n \ne x_0\]

Таким образом, обратимость очень интересное свойство функций, сохраняющее монотонность и непрерывность. А в заключение поста надо познакомиться с еще одним важным понятием, позволяющим ввести классы эквивалентности для функций.

Классы сравнения функций

Видно, что значения этих функций стремится к нулю при аргументе стремящемся к нулю. Но насколько быстро? Обгоняет ли одна функция другую при стремлении к нулю? Или они одинаково быстры? Для того, что бы иметь возможность отвечать на такие вопросы вводят классы сравнения функций. Сначала рассмотрим эквивалентные функции:

Рассмотрим еще один класс сравнения функций называемый о-малое.

\[\exists C\in \mathbb \ \ \forall x \in \stackrel>(x_0) \to |f(x)| \leq C|g(x)|\]

Источник